Le varie zecche europee, coniavano, fino a tutta la metà del XIII secolo, solo piccole monete ottenute dividendo una libbra da ν once in 240 monetine chiamate denari piccoli o pisanini, se coniati a Pisa, o genovini se a Genova o, per una generica moneta, semplicemente "denari". Nei conti economici e per tutte le monete, a partire da Carlo Magno, 12 denari davano luogo a 1 soldo e 20 soldi a una lira, chiamata anche libbra (in latino il termine libra indica sia il peso che il valore monetario) essendo una lira equivalente, in peso, a una libbra di una lega contenente ν once di argento, l'ipotesi di omogeneità della lega implica che ogni denaro coniato ha la stessa quantità di argento data da

ν

240 once. La qualità delle monete era molto variabile passando da poco più di 4 nel 1164 (33,3% di argento) fino a 1 nel 1202 (8,3 %). "I denari pisani fino alla prima metà del ‘200".

Il capitolo XI del Liber abaci è interamente dedicato alla fusione di monete di qualità diverse e al modo di ottenere monete di una data qualità fondendo tra loro monete di varia tipologia. La matematica sottostante a questi problemi riguarda i sistemi di equazioni lineari in due o più incognite che in questo modo vengono introdotti nella storia della matematica in occidente sul modello delle ricerche che gli arabi avevano iniziate tempo addietro.

Un primo problema proposto da Fibonacci consiste nel trovare quanta moneta da w once si può ottenere fondendo una data quantità a di monete da v once senza aggiungere argento ma aggiungendo o levando il rame a seconda che la qualità che si vuole ottenere sia migliore o peggiore della precedente.

Il metodo risolutivo si svolge naturalmente passo dopo passo calcolando prima la quantità di argento contenuta nelle 7 libbre che, essendo da 5 once, darà luogo a 35 once con le quali, dividendo per 2, si ottengono 17

1

2 once che permettono di fare una lega del peso di 17

1

2 libbre da 2 once aggiungendo il rame che manca. Poiché la seconda lega ha tutto l'argento e tutto il rame della prima lega che pesa 7 libbre, dobbiamo aggiungere il rame che serve per arrivare al peso di 17

1

2 libbre, il rame da aggiungere sarà dato semplicemente da 10

1

2 libbre. Come si vede la soluzione di questo problema usa la linearità della quantità di argento in un dato peso e il significato delle operazioni di moltiplicare, dividere e sottrarre.

Le cose diventano più complicate quando dobbiamo lavorare con due o più leghe ognuna di valore diverso. L'uso del calcolo algebrico e la possibilità di indicare con delle lettere dei generici numeri operando con quelle lettere come fossero numeri con le regole dell'Algebra facilita di molto il pensiero che trova nella scrittura un validissimo supporto anche visivo e mnemonico. Anche la "cosa", all'apparire dell'Algebra nel capitolo XII del Liber abaci, non avrà una scrittura formale con una propria lettera ma sarà sempre nel calcolo algebrico parlato (e scritto) la "cosa". In questo confine, che vede da un lato il ragionare concreto su oggetti reali e dall'altro gli albori del calcolo algebrico astratto, risalta con estrema chiarezza quanto si guadagni in generalità e semplicità con l'Algebra astratta, ma anche quanto pensiero puro, non formalizzato, non meccanico si perda; quanta fatica intellettuale sia necessaria per raggiungere determinati risultati che in poco si potrebbero raggiungere servendoci delle x e delle y. Fibonacci è su questo confine e il suo lavoro ci fornisce un esempio concreto delle possibilità e della forza del pensiero pre-algebrico e, nello stesso tempo, ci fornisce degli esempi, che nell'evidenziare le difficoltà cognitive, apre la strada e giustifica il salto successivo, nel mondo dell'Algebra, così importante nella formazione matematica di un allievo. In particolare, nel capitolo XI del Liber abaci troviamo dei sistemi di equazioni lineari in due o più incognite (anche 240 ! [XI.6.17]) che Fibonacci analizza e risolve in modo diretto servendosi di un pensiero concreto e nello stesso tempo immaginifico a nostro avviso di grande interesse. Si tratta di argomenti da tempo trattati con grande profondità dai matematici arabi e, tra questi, come vedremo anche più avanti, spicca il nome di Abu Kamil  [RR]

Roshdi Rashed,
Abu Kamil, Algèbre et Analyse Diophantienne,

(IX sec. d.C.) il grande matematico egiziano che diede all'algebra di al-Kwarizmi una sistemazione rigorosa e generale, noto probabilmente anche a Fibonacci attraverso una traduzione latina della sua opera

Il problema dei monetieri consiste essenzialmente nel decidere a priori in quali quantità si debbano fondere tra loro due o più leghe di diversa qualità per realizzare delle monete di qualità determinata. Ciò che si conosce è la qualità delle leghe a disposizione e si cerca la quantità di metallo di ogni singola lega che si deve fondere per ottenere la qualità voluta.

Vi sono dunque dei numeri noti che sono le qualità delle leghe che si vuol fondere e che quindi saranno scritti e indicati col loro valore numerico ma anche delle incognite che non si conoscono a priori che sono le quantità di materiale da fondere per ottenere la lega voluta e che lui indica come calcolare attraverso un algoritmo che opera sui numeri noti.

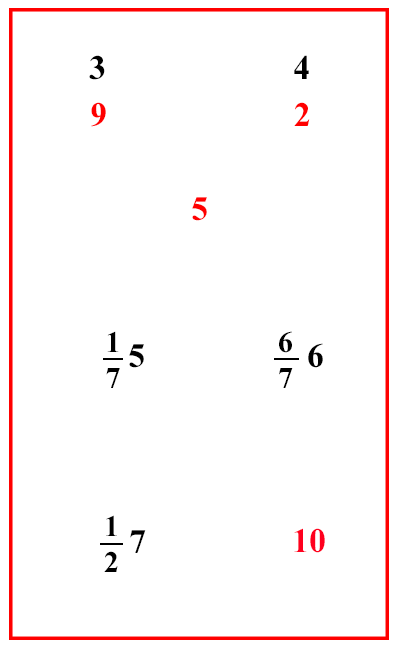
Consideriamo il primo esempio proposto da Fibonacci [XI.6.1] che riguarda il caso nel quale si vuole realizzare una lega di valore intermedio tra i due valori delle due leghe assegnate. Nello specifico, abbiamo due leghe, una da 2 once e un'altra da 9, e vogliamo fare una lega da 5 once. Se ad esempio mettiamo 1 libbra di ciascuna lega otteniamo 11 once di argento in 2 libbre quindi una lega da 5

1

2 mentre vogliamo ottenere una lega da 5 once. Se indichiamo con x₁ la quantità in libbre di lega da 9, allora l'argento che otteniamo da questa fusione sarà di 9

x₁ once mentre, indicando con x₂ la quantità in libbre di lega da 2, da questa fusione otteniamo 2

x₂ once d'argento e unendo insieme le due quantità otteniamo x₁

+

x₂ libbre di minerale che contiene 9

x₁

+

2

x₂ once d'argento. Volendo che questa fusione contenga 5 once d'argento per ogni libbra sarà necessario avere

Fibonacci, che non è in grado di scrivere questa equazione, ma fornisce un semplice algoritmo che opera sui valori iniziali noti, i soli che può scrivere, cioè sui numeri 2, 9 e 5 e indica una serie di operazioni da fare con questi numeri per ottenere il risultato voluto. Descrive anche un diagramma che riassume, per aiutare la memoria, il da farsi in ogni problema analogo e, infine, giustifica il suo algoritmo con un convincente ragionamento non formalizzato.

Ecco l'algoritmo [XI.6.1]:
Ecco il diagramma:
Il diagramma indica anche in nero il risultato che fornisce l'algoritmo nell'ipotesi aggiuntiva che si vogliano realizzare 12 libbre di lega da 5 once e, più in basso quanto si debba aggiungere della lega da 9 once se si decide di usare 10 libbre di monete da 2. La soluzione del primo problema si ottiene fondendo 3 parti della lega da 9 e 4 parti della lega da 2 e, volendo realizzare 12 libbre, si dovrà dividere 12 in due parti proporzionali a 3 e 4 cosa che è stata trattata precedentemente e che comunque è facile da realizzarsi e fornisce i valori 5

1

7 per la lega maggiore 6

6

7 per quella minore. Se poi si dispone di 10 libbre della lega minore e si vuol sapere quanto si deve mettere della maggiore per ottenere una lega da 5, basterà trovare un numero che rapportato a 10 sia come 3 rapportato a 4 numero che si ottiene ovviamente moltiplicando 3 per 10 e dividendo per 4.

Ecco la giustificazione (dimostrazione?) dell'algoritmo [XI.6.1]:

Spiega Fibonacci: mettendo 3 libbre della moneta da 9 si ottengono 27 once d'argento mentre, volendo fare monete da 5, ne dovrebbero contenere 15 abbiamo quindi 12 once in più di argento. Questo surplus viene compensato mettendo 4 libbre della moneta da 2. Queste 4 libbre contengono 8 once d'argento mentre, volendo fare monete da 5, ne dovrebbero contenere 20: ne mancano quindi 12 che sono compensati dai 12 in più derivanti dalla lega maggiore. Ma, a ben guardare, questo ragionamento ha un valore generale non legato dai numeri in gioco che vogliamo illustrare parola per parola usando dei simboli per i numeri in gioco (peraltro non necessari) per aiutare il lettore. Siano ν₁ > ν₂ i valori delle due leghe che vogliamo fondere e sia ν    (ν₁ > ν > ν₂) il valore della lega che si vuole realizzare. Ogni libbra da ν₁ once contiene ν₁-ν once d'argento in più, mentre ogni libbra da ν₂ once contiene ν-ν₂ once di argento in meno. Quindi se fondiamo ν-ν₂ libbre della lega maggiore abbiamo un surplus di argento pari (ν-ν₂)×(ν₁-ν) ma se a questo aggiungiamo la fusione di ν₁-ν libbre della lega minore abbiamo una mancanza di argento di (ν₁-ν)×(ν-ν₂) compensato esattamente dal surplus prodotto dalla lega maggiore proprio perché Così prosegue Fibonacci:
Infatti se prendiamo un multiplo (o una parte) delle ν-ν₂ libbre della lega maggiore e lo stesso multiplo (o parte) delle ν₁-ν libbre della lega minore avremmo lo stesso multiplo (o parte) dell'argento contenuto in queste leghe ma anche lo stesso multiplo (o parte) della quantità di materiale ottenuto dalla fusione di queste due leghe ragion per cui la sua qualità non cambia.

Col linguaggio astratto dell'algebra tutto questo pensiero fatto di argento luccicante, minerali che si fondono e si mischiano tra loro, equilibrio tra il troppo e il troppo poco, si riduce a semplici cieche operazioni

perché, per ogni k, 4

(3

k) = 3

(4

k).
Vi sono infiniti modi di scegliere le due quantità di monete da 2 e da 9 per realizzare una lega da 5 che è come dire che l'equazione 9

x₁ + 2

x₂ = 5

(x₁ + x₂) ha infinite soluzioni che dipendono linearmente da un parametro k. Una ulteriore condizione come x₁ + x₂ = 12 o x₁ =10 individua una soluzione unica.

L'immagine, il racconto, il ragionamento sulla fusione di due tipi di monete diventa in Fibonacci il prototipo di un problema molto più generale riducibile a quello e al suo metodo risolutivo.

Il problema si allarga immediatamente al caso che le monete da fondere siano più di due diventando man mano che il pensiero prosegue sempre più ricco di soluzioni e di varianti. Fondere tre monete da 3, 4, 6 once per ottenere una moneta da 5, oppure 4 monete di vario valore [XI.6.10] o anche 7 monete [XI.6.13]. In questi casi vi sono infinite soluzioni dato che le incognite sono più del numero di condizioni e Fibonacci descrive diversi metodi per trovare queste soluzioni. In un primo tempo suggerisce di fare due monete: una fondendo quelle che hanno valore più piccolo del valore ν che si vuole ottenere e l'altra fondendo quelle che hanno un valore maggiore. Fatto questo, si fondono queste due leghe con l'algoritmo precedente ottenendo una moneta di valore ν: una fusione di fusioni! Ma suggerisce anche un secondo metodo completamente diverso, che letto in termini moderni è molto significativo. Si fondono coppie di monete in una sola moneta del valore cercato ν. In questo modo di ottengono tante monete in diverse quantità ma tutte di valore ν, sommando queste monete, cioè fondendole tutte insieme in opportune proporzioni si possono ottenere diverse soluzioni al problema iniziale, dal momento che, se si fondono in proporzioni arbitrarie monete dello stesso valore ν si ottengono sempre monete di valore ν. In termini moderni questa strategia è estremamente interessante perché prefigura una idea importante che si utilizza oggi per risolvere sistemi di equazioni lineari omogenei: si cercano soluzioni particolari e poi si combinano linearmente le soluzioni trovate. Più precisamente, abbiamo n monete da ν₁, ν₂, ... , ν_n once e vogliamo con esse fare una lega che contenga x₁ libbre di monete da ν₁ once, x₂ libbre di monete da ν₂, ... , x_n libbre di monete da ν_n once, in modo che la lega ottenuta sia da ν once. Questo problema conduce all'equazione:
si tratta di un sistema lineare omogeneo di 1 equazione in n incognite. Fibonacci, se n > 2, calcola n-2 soluzioni particolari fondendo coppie di monete una col valore maggiore di ν e l'altra col valore minore. Combinando linearmente queste soluzioni può trovare soluzioni generali del sistema. Nel caso [XI.6.10] vi sono monete da 2, da 3, da 6 e da 7 once a libbra e si vuole vedere come è possibile ottenere 19 libbre di monete da 4 fondendo insieme quantità opportune e da determinare, di queste quattro tipologie di monete. In questo caso l'equazione è
e Fibonacci calcola 3 soluzioni particolari : P=(3,0,0,2), S= (0,2,1,0), T= (1,0,1,0) fondendo coppie di monete per ottenere monete dello stesso valore 4. Nel primo caso P ottiene 5 libbre (3 da 2 once e 2 da 7) da 4 once, nel secondo 3 libbre (2 da 3 e una da 6) da 4 once e nel terzo 2 libbre da 4 (una libbra da 2 e una libbra da 6). Per ottenere complessivamente 19 libbre da 4 once, cioè per verificare l'ulteriore condizione prende la soluzione 2

P + S + 3

T.

La cosa didatticamente interessante è che questo tipo di problemi ha infinite soluzioni e non una unica soluzione, soluzioni che possono essere ottenute seguendo diverse strade. Il pensiero è libero di trovare strategie diverse tutte possibili e vincenti lasciando spazio all'insegnante per sviluppare negli studenti lo spirito critico basato sul confronto delle scelte liberamente, ma non casualmente, fatte. Alla fine, nasce un gioco surreale, una sfida apparentemente impossibile, non più per monetieri ma per matematici dove mettere alla prova la propria abilità:

Alla fine le monete, le leghe, la fusione dei metalli, svaniscono dall'orizzonte, ma resta un modello, il prototipo di un metodo, di una "cultura" quella delle monete, con la quale è possibile risolvere varie questioni che con le monete non hanno più nulla a che fare.

Osserviamo intanto che ogni sistema di due equazioni lineari in due incognite che abbia la forma può interpretarsi, se a è diverso da b e A diverso da zero, come un problema di fusione di monete.
Supponiamo di avere delle monete da a once e delle monete da b once e supponiamo di voler fondere opportune quantità di quelle monete per ottenere una lega da

B

A once. L'algoritmo di Fibonacci fornisce, a calcoli fatti, la soluzione
naturalmente il parallelo con le monete diventa effettivo se i numeri in gioco sono tutti positivi e i valori sono minori di 12. L'immagine, il racconto, il ragionamento sulla fusione di due tipi di monete diventa in Fibonacci il prototipo di un problema molto più generale riducibile a quello e al suo metodo risolutivo.

Nel problema [XI.7.1] citato sopra abbiamo ovviamente

I problemi successivi nel Liber abaci si riducono tutti alla "cultura delle monete" e trattano di mele e pere, vari tipi di selvaggina, del calcolo di un giusto salario, di un uomo che compra a Costantinopoli 90 moggi di biade varie o di come fare una campana con 5 metalli diversi che hanno prezzi diversi, ma, il problema finale di un uomo che compra 30 uccelli di tre tipi per 30 denari, apre, anche in occidente, un nuovo campo di ricerca estremamente interessante: la così detta analisi indeterminata. Si tratta del famoso problema "dei cento uccelli" formulato in Cina (Zhang Qiujian) nel V secolo (e forse anche prima) giunto in India (Bakhshali) nel VII, tra i matematici arabi nel IX e, infine, in Europa nel Liber abaci di Fibonacci nel XII secolo.

La formulazione cinese riportata nel libro di Zhang Qiujian è la seguente:
Il problema ha tre soluzioni in numeri interi positivi che il matematico cinese riporta integralmente: indicando come primo numero quello dei galli, come secondo quello delle galline e come terzo quello dei pulcini, le tre soluzioni sono (4,18,78), (8,11,81), (12,4,84).

In generale il problema ha questa forma: vi sono diverse qualità di uccelli ognuna delle quali ha un certo prezzo e si vuole sapere quanti uccelli di ciascun tipo sono stati acquistati sapendo che in tutto si è speso per 100 uccelli 100 denari. Il problema consiste dunque, dati i numeri razionali (positivi) a₁, a₂, ... , a_n e il numero positivo A, trovare, se esistono, n numeri interi incogniti x₁, x₂, ... , x_n che verificano le condizioni:

E' chiaro che, essendo il problema relativo all'acquisto di uccelli, e non potendo acquistare una frazione di uccello, le soluzioni che si cercano devono essere espresse in numeri interi e positivi. Si tratta dunque di un problema indeterminato che rientrerà nella grande classe di problemi diofantei all'origine di una nuova branchia della matematica: la teoria dei numeri. E' anche chiaro che il problema, se non è impossibile, ha un numero finito di soluzioni essendo finito il numero di modi di scrivere un numero A come somma di n numeri interi positivi (numero certamente minore di Aⁿ ).
Abu Kamil, il matematico arabo successore di Al-Khwarizmi, dopo aver studiato e risolto alcuni casi trovando tutte le soluzioni possibili, decide di scrivere un piccolo trattato Sui volatili, oggi noto col titolo I problemi rari di aritmetica  [RR]

Roshdi Rashed,
Abu Kamil, Algèbre et Analyse Diophantienne,

. In quel trattato propone 6 problemi, uno impossibile e gli altri con diversi numeri di soluzioni ed, infine, nel caso seguente calcola 2676 soluzioni indicando al lettore, attraverso delle opportune tabelle, come arrivare a questo risultato! Un semplice programma al calcolatore, scritto in Python, che il lettore può trovare in Appendice, ha permesso oggi di verificare il calcolo e abbiamo potuto riscontrare che le soluzioni sono 2678, appena 2 in più a quelle trovate da Abu Kamil nel IX secolo. Il risultato fece all'epoca molto scalpore anche perché il problema dei 100 uccelli come ci dice lo stesso Abu Kamil era molto popolare
In generale il procedimento di Abu Kamil consiste nel ricavare una incognita da una equazione sostituirla nell'altra e ridurre il problema a una sola equazione lineare che viene risolta con numeri interi usando criteri di divisibilità.

Il problema dei 100 uccelli è trattato da Fibonacci alla fine del capitolo XI del Liber abaci con degli esempi sia nel caso di 3 tipologie di uccelli che di 4. La cosa interessante è che il metodo utilizzato da Fibonacci è diverso da quello che troviamo in Abu Kamil ed è straordinariamente vicino ai moderni metodi di algebra lineare usati oggi per risolvere sistemi di equazioni di primo grado. Per questo è interessante vedere più da vicino il metodo utilizzato da Fibonacci. Come prima cosa il problema viene inquadrato nella “cultura delle monete”: il sistema iniziale viene riletto come riducendo quindi la questione al problema di fondere n tipi di monete da a₁, a₂, ... , a_n once a libbra rispettivamente per ottenere A libbre di una moneta da 1 oncia a libbra. La cosa importante è che ora la prima equazione è omogenea e oggi sappiamo che le soluzioni di un sistema omogeneo di equazioni lineari (in questo caso una equazione in n incognite) formano uno spazio vettoriale cosa che permette di scrivere ogni soluzione come combinazione lineare di alcune soluzioni particolari: quelle che danno luogo a una base dello spazio. Nel caso specifico di una sola equazione, una base è formata da (n-1) soluzioni particolari. Il metodo seguito da Fibonacci, come vedremo dettagliatamente più avanti, consiste nel calcolare esplicitamente una base e, successivamente, cercare quale combinazione lineare di quella base verifica la prima equazione (quella non omogenea) trovando così, nei casi più semplici tutte le soluzioni intere o l'incompatibilità del sistema.

Vediamo ora, passo passo, come procede Fibonacci nel caso di tre tipologie di uccelli

Usando le nostre notazioni dobbiamo risolvere con numeri interi positivi simultaneamente le due equazioni Ancora Fibonacci: cioè: e moltiplicando per 2 abbiamo Fibonacci continua:
col metodo della fusione di due monete trova una prima soluzione particolare P=(1,0,4) cioè una penice e 4 passeri e una seconda soluzione particolare S=(0,1,2) cioè una colomba e 2 passeri. Col nostro linguaggio P ed S formano una base per lo spazio delle soluzioni. Ora Fibonacci fa una “fusione di fusioni” per trovare una soluzione con 30 uccelli e verifica che 3

P+5

S, cioè 3 pernici, 5 colombe e 22 passeri, risolve il problema. Col nostro linguaggio, Fibonacci trova una combinazione lineare delle due soluzioni particolari che verifica la prima condizione.
Poi, senza giustificare le sue affermazioni forse perché all'epoca facili da verificare, specifica:

In effetti, una soluzione dell'equazione omogenea è ottenuta combinando le due soluzioni trovate a

P + b

S = (a,b,4

a+2

b) e il totale degli uccelli è 5

a + 3

b con a e b interi positivi perché cerchiamo soluzioni intere. Inoltre, se A è il numero di uccelli, l'equazione
può essere sempre risolta in più di un modo se A

>

15. Infatti, dividendo A per 5, abbiamo Dunque per q

>

2 cioè per A

>

15 il sistema ha sempre almeno una soluzione. Facilmente si vede anche che, se A

<

15, si ottiene una soluzione solo nei casi A = 13, 11, 8. Osserviamo che in questo modo abbiamo trovato un metodo per risolvere anche il sistema in 4 incognite che si riduce all'analisi precedente ponendo A

=

100

-

x₄ : abbiamo almeno una soluzione per 100

-

x₄>

15 cioè per 0 < x₄ < 85, e anche per i valori x₄ = 92, x₄ = 89, x₄ = 87. Quindi il sistema ha almeno 87 risposte corrette. Per trovare il numero esatto di soluzioni occorre trovare il numero di soluzioni intere dell'equazione 5

a + 3

b = A cosa nota ai matematici indiani (Brahmagupta, VII sec. a.C.), arabi e forse anche a Fibonacci.

In Appendice abbiamo discusso questo problema usando un calcolatore che ci permette di trovare tutte le soluzioni e verificare le affermazioni di Fibonacci.

L'esempio cinese è molto simile a questo perché l'equazione omogenea che risulta ha le due soluzioni particolari P=(1,0,6) e S=(0,1,3) e ogni soluzione intera si scrive sempre come a

P + b

S con a e b interi positivi.

L'esempio successivo in Fibonacci [XI.7.14] mostra un caso simile di tre tipi di uccelli dove si chiede che la somma di tutti gli uccelli sia 12. In questo caso Fibonacci trova due soluzioni particolari dell'equazione omogenea date da P =(3,0,4) e S=(1,2,0) e la soluzione generale è e, per avere soluzioni intere è non è più necessario avere a e b interi infatti affinché 2

b sia intero si può avere anche b

=

p

2, infatti la soluzione è

3

2P

+

1

2S. Anche se l'analisi è un po' più complicata dovendosi considerare per a e b anche delle frazioni, tuttavia il metodo è facilmente praticabile anche in questo caso (vedi Appendice).

Ma l'esempio più interessante, molto simile allo spettacolare esempio di Abu Kamil, è l'ultimo [XI.7.15]. Si tratta di 4 tipologie di uccelli e di 4 coefficienti diversi da 1. In questo caso le soluzioni dell'equazione omogenea sono generate da tre soluzioni particolari indipendenti e l'analisi è più complessa. Intanto Fibonacci calcola, diremo oggi, una base per lo spazio delle soluzioni.
In altri termini, Fibonacci trova due soluzioni indipendenti: la prima soluzione P=(3,0,0,8) è ottenuta “mettendo in lega” pernici e passeri e la seconda S= (0,1,2,0) tortore e colombe, ma le combinazioni a

P + b

S non possono produrre 30 uccelli dato che 11

a + 3

b = 30 non ha soluzioni intere se a e b sono interi positivi e questo non significa che il problema è impossibile perché, come diremo oggi, P e S sono linearmente indipendenti ma non generano lo spazio delle soluzioni. Fibonacci trova altre due soluzioni indipendenti da quelle T=(0,3,0,4) e Q=(1,0,4,0):
può a questo punto calcolare diverse possibili soluzioni combinando linearmente P, S e T o anche P, T e Q. In effetti trova le soluzioni 2

P

+

S

+

Q

=

(7,1,6,16) e P

+

2

T

+

Q

=

(4,6,4,16). Nella Appendice discutiamo questo problema con l'aiuto di un calcolatore che ci permette di trovare tutte le 19 soluzioni del problema proposto da Fibonacci. Se, invece di 30 uccelli chiediamo di comprarne 100 con i medesimi prezzi le soluzioni sono 238!

Non possiamo certo affermare che Fibonacci avesse compreso il fatto che ogni possibile soluzione di una equazione lineare e omogenea in 4 incognite si possa sempre esprimere come combinazione lineare, a coefficienti razionali, di 3 soluzioni linearmente indipendenti e che P, S e Q formano una base per lo spazio delle soluzioni, tuttavia sull'esempio della fusione di monete, si comporta nei suoi calcoli come ci comporteremo noi oggi con le nostre conoscenze sugli spazi vettoriali e sulle loro basi.

E’ interessante pensare che questa frase con cui conclude il capitolo [XI.7.15] si riferisca, con una certa ironia, ai problemi trattati da Abu Kamil che sono quasi tutti di questo tipo, nella consapevolezza, forse, di avere un metodo più efficace di quello del grande matematico arabo.

In Appendice trattiamo i problemi che presenta Fibonacci risolti in generale con l’uso di un calcolatore e con lo stesso programma troviamo le soluzioni ai 6 casi proposti da Abu Kamil.