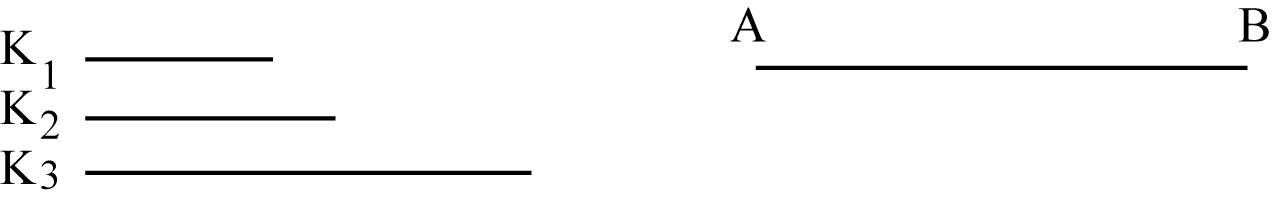|
Ladri, maiali e cammelli Franco Ghione - Sandro Moriggi |

| |
|
Sono tre ladri che vanno a rubare com patto dacordo che uno di loro sia quello che rubi, un altro faccia la guardia, l’autro debbe vendere quello che si ruba et vogliono che, quello che si ruba , quello che lo ruba n’abbia il
12 et quello che fa la guardia n’à a avere il
13 et quello che vende n’à avere il
14. Aviene che le vendoro 1000 fiorini larghi; addimandasi quanto tocha a ciascuno a ciò che tuttj habbino loro dovere.
[F. Calandri, Aritmetica, 1492]
| |||||||||||||||

|
|||||||||||||||
|
Consideriamo n soci ognuno dei quali investa una determinata quantità di denaro: siano a1, a2,..., an le somme investite, queste, messe insieme, formano il capitale
A = a1 + a2 +...+ an
che, una volta investito, produce un profitto p(A). Si vuole vedere quanto di questo spetti al singolo investitore [Liber abaci, cap. X].
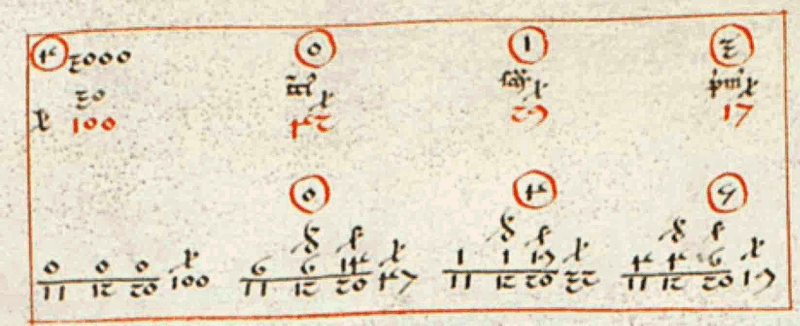
(X.11) Tre uomini fecero una società: il primo di essi mise 17 lire, il secondo 29 lire, il terzo 42 lire; e furono guadagnate 100 lire
 |
|||||||||||||||
|
Si chiede come vanno divise tra i tre soci le 100 lire guadagnate. In questo tipo di problema si considera il capitale A investito in una singola operazione, analogo a una lega di rame e argento [Liber abaci, cap IX] dove i due metalli sono amalgamati così bene che è lecito supporre che la quantità di argento p(a) (guadagno) contenuta in una parte a (singolo investimento) di quella lega conservi i multipli, cioè un peso doppio di quella lega contiene il doppio di argento, un peso triplo il triplo di argento ecc. in formule :
p(n × a)=n × p(a) per ogni n
cosa che ci permette di affermare che la quantità p(a) di argento di quella specifica lega, dipende linearmente da a. La stessa situazione si ritrova nel caso del peso specifico dove il peso p(a) di un volume a di un singolo materiale dipende linearmente da a. E’ la stessa aritmetica si ritrova nel caso dei moti equabili, quei movimenti per i quali lo spazio p(a) percorso nel tempo a dipende linearmente da a, situazione che si può ipotizzare ogni volta che il risultato p(a) di una determinata azione compiuta nel tempo a produce in tempi doppi risultati doppi in tempi tripli risultati tripli ecc. come ad esempio il numero p(a) di alberi piantati nel tempo a da una determinata squadra di giardinieri (IX.3.8). |
|||||||||||||||
|
Anche in una società di investitori possiamo supporre che il guadagno p(a) di ciascuno sia, per così dire, uniformemente distribuito cioè che un investitore che abbia investito il doppio abbia un guadagno doppio, uno che ha investito il triplo un guadagno triplo ecc. di modo che si possa considerare lineare la relazione tra a e p(a). In ognuna di queste situazioni |
|||||||||||||||
|
p(a 1)p(a 2) =
a 1a 2
|
e quindi il rapporto (quoziente tra due numeri) |
p(a1)a1 = p(a2)a2 | |||||||||||||
|
non dipende da a ma definisce un valore caratteristico di quel tipo di investimento che potremmo chiamare il suo rendimento. Se l’investimento è misurato in lire, come al tempo di Fibonacci, il rendimento k di un determinato investimento è il guadagno prodotto da una lira k =
p(a)a =
p(1)1
e quindi l’espressione analitica della funzione p è semplicemente
p(a) = k×a
| |||||||||||||||
|
In ogni situazione considerata sopra, questo rapporto caratteristico assume nomi diversi: il titolo in una moneta ottenuta da lega di rame e argento, il peso specifico nel caso di materiali omogenei, la velocità nel caso dei moti uniformi. Ovviamente questa presunta omogeneità è una ipotesi alla base del modello matematico che viene costruito, ipotesi da tutti condivisa che permette di sviluppare dei calcoli precisi. E anche si potrebbe ugualmente pensare, legittimamente, che, per motivi di giustizia sociale, il rendimento di un dato investimento debba essere distribuito in modo diverso creando modelli matematici alternativi che privilegino gli investitori più poveri e quindi più bisognosi di guadagni. In ogni caso il modello matematico basato sull’ipotesi di uniformità, finisce per definire una idea di giustizia, di affermare cioè in che modo è giusto dividere gli utili di una data compagnia idea che diventa alla fine da tutti condivisa e che ha il vantaggio di sciogliere, attraverso calcoli precisi, eventuali contenziosi. |
|||||||||||||||
|
Tornando al problema iniziale, nell’ipotesi di linearità, il rendimento di quel dato investimento è dato da
p(A)A =
p(ai)ai e quindi il profitto p(ai) che spetta ai diversi soci è:
p(a1)=
p(A)×a1a1 + a2 +... + an ,
p(a2)=
p(A)×a2a1 + a2 +... + an , ... ,
p(an)=
p(A)×ana1 + a2 +... + an ,
| |||||||||||||||
|
Tornando al problema [Liber abaci X.11] dei tre investitori, visto il contesto e il forte interesse di ogni socio a che la divisione non penalizzi nessuno, Fibonacci indica la soluzione con la massima cura utilizzando anche la prova del 7, cioè verificando l’esattezza del calcolo modulo 7, visibile nelle cifre contornate da un cerchietto rosso. La frazione
10088 che rappresenta il rendimento di quell’investimento e guadagni dei singoli soci sono espressi, con grandissima precisione, esprimendo il risultato in lire, soldi (
120 di una lira) e denari (
112 di un soldo) e anche (per futura memoria?) in 11 parti di un denaro. A calcoli fatti, al primo socio spettano 19 lire 6 soldi 4 denari e
411 di denaro poco meno di mezzo denaro.
Possiamo ritrovare questo risultato, come vedremo, usando una animazione ottenuta con GeoGebra. | |||||||||||||||
|
|
|||||||||||||||
|
Nei problemi che riguardano le divisione di utili tra n consoci il guadagno complessivo p(A) è diviso in n parti p(a1), p(a2), ... , p(an) proporzionali ad a1 , a2 , ..., an tali che
p(A)= p(a1) + p(a2 ) + ... + p(an)
Ne nasce un ulteriore problema analogo, questa volta un problema astratto, di matematica pura che permette di risolvere come casi particolari infiniti problemi specifici:
La divisione proporzionale
Dato un insieme di n numeri {a1, a2, ..., an} e numero B, trovare un secondo insieme di n numeri {b1, b2, ..., bn} proporzionali rispettivamente ad {a1, a2, ..., an} tali che
B = b1 + b2 + ... + bn
Definizione
n numeri {b1, b2, ..., bn} sono proporzionali rispettivamente ai numeri {a1, a2,..., an} se i rapporti tra due qualsiasi numeri
ai : aj = bi : bj per ogni coppia (i,j).
Questa condizione si verifica se e solo se esiste un numero k tale che bi = k × ai per ogni indice i. Infatti se ai × bj = bi × aj per ogni i e j allora
aibi =
ajbj
cioè il rapporto k tra due numeri corrispondenti è lo stesso. Nell’esempio precedente i numeri {p(a1), p(a2), ..., p(an)} sono proporzionali ai numeri {a1, a2,..., an} proprio perché p(ai) = k × ai e quindi il problema si riformula chiedendo di dividere il guadagno p(A) proporzionalmente ai singoli investimenti.
| |||||||||||||||
|
Fibonacci formula in modo più esplicito la divisione proporzionale in un nuovo problema che può creare difficoltà e meraviglia a quelli inesperti [ "Il problema del maiale" Liber abaci, cap. X.17 ] con grande chiarezza e attenzione didattica.
C'erano quattro uomini, il primo dei quali mise
13 di un intero, un altro mise
14, il terzo mise
15, il quarto poi mise
16; e ebbero insieme 60 soldi; ci si chiede quanto spetti a ciascuno di questi 60 soldi. Questo in realtà è il problema che si pone nel caso in cui quattro uomini, che hanno acquistato un maiale per 60 soldi, vogliano avere: il primo un terzo di quel maiale, il secondo un quarto, il terzo un quinto, il quarto un sesto. Perciò pagando il primo 20 soldi, per la terza parte del maiale, e il secondo, per la quarta parte, 15 soldi, e il terzo, per la quinta parte, 12 soldi, e il quarto per la sesta parte 10 soldi, e tutte queste somme insieme ammontano soltanto a 57 soldi, coloro che non sono competenti si meravigliano che rimangano da pagare 3 soldi dei 60 soldi; e chiedono chi di loro debba pagare quei 3 soldi. Infatti non considerano, che questi quattro uomini non comprarono tutto il maiale, perché
16
15
14
13 di un intero non fanno un intero, ma ne rimane
120. Perciò dei 60 soldi ne resta similmente la ventesima parte, cioè 3 soldi. Per cui se ci fossero tre uomini, dei quali il primo comprasse la metà di quel maiale, e pagasse 30 soldi; e un altro comprasse un terzo, e pagasse 20 soldi, e un terzo comprasse un quarto, e pagasse 15 soldi; così si avrebbero avuto in totale 65 soldi, cioè 5 soldi in più dei 60 soldi ; questi 5 soldi sono la dodicesima parte di 60 soldi. e questo capita perché
14
13
12 fanno un dodicesimo più di un intero. E quindi per non pagare più o meno dei 60 soldi, conviene che i compratori, quanti che siano stati, comprino le parti che, quando saranno sommate insieme, facciano un intero. Per esempio: se i compratori fossero due, uno compri la metà, e l'altro l'altra metà; o uno
23 e l'altro
13, e cosi via. E se fossero tre ciascuno compri un terzo, oppure il primo ne compri
12, il secondo
13, il terzo
16. E se fossero quattro, ciascuno compri un quarto, oppure il primo compri
12, il secondo
14, il terzo
15, il quarto
120, e così puoi intendere in più casi.
La soluzione generale del problema della divisione di B in n parti proporzionali ad a1, a2,..., an si ottiene in modo analogo a come si è fatto nella divisione degli utili tra n consoci: dobbiamo ottenere
bi = k×ai
e il valore di k che ci manca si ottiene tramite una divisione dovendo avere
B = b1 + b2 + ... + bn
B = k×a1 + k×a2 + ... + k×an = k×(a1 + a2 + ... + an)
e quindi
k = Ba1 + a2 + ... + an e bi = k × ai La soluzione non cambia se si sostituiscono i valori a1, a2, ..., an con loro equi multipli m×a1, m×a2, ..., m×an che possono essere scelti a piacere per risolvere il problema. |
|||||||||||||||
|
|
|||||||||||||||
|
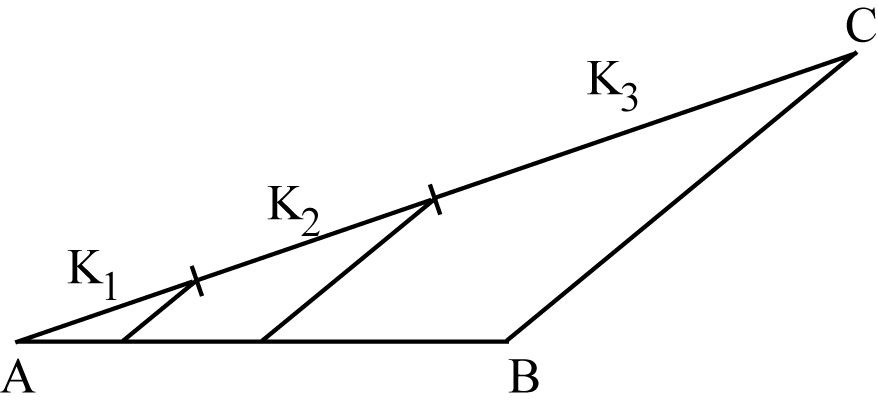
Dividere un dato segmento AB in n parti proporzionali a n dati segmenti K1, K2, ..., Kn . Soluzione: si costruisce il segmento AC = K1 + K2 +... + Kn , si congiunge B con C e si tracciano le rette parallele a BC.
Questo punto di vista ci permette di creare un software con GeoGebra, realizzato da Sandro Moriggi, che permette di risolvere geometricamente questo tipo di problema ( |
|||||||||||||||
|
Soluzione geometrica del problema del maiale.
Scegliamo al posto di 13, 14, 15, 16 i multipli 603, 604, 605, 606 cioè 20, 15, 12, 10 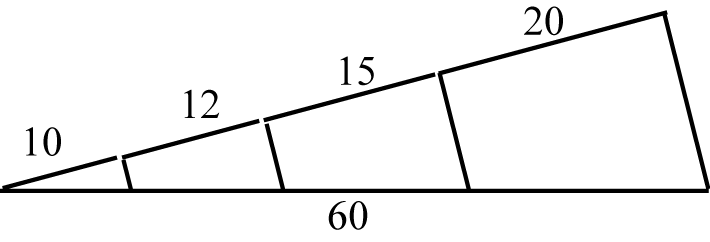
Per calcolare il valore numerico delle singole parti abbiamo k =
6057 =
2019 e quindi le parti sono:
Sommando viene 59,98 mancano 2 centesimi: chi li deve pagare? | |||||||||||||||
|
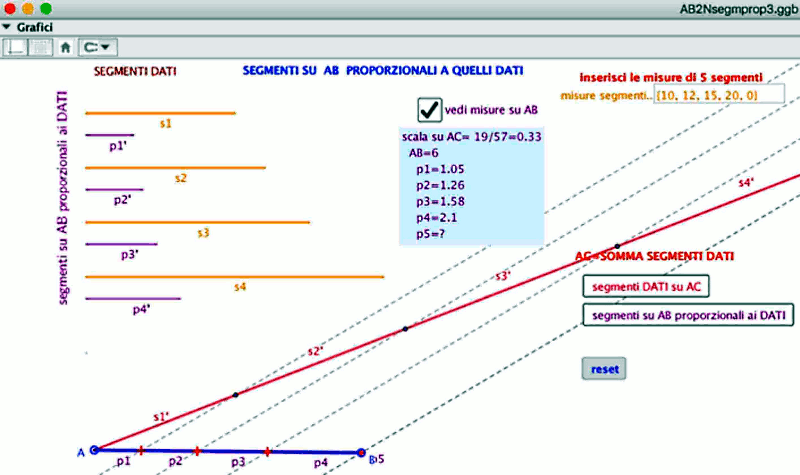
Usando il nostro geogebra per risolvere il problema,
Ovviamente avremmo anche potuto rendere AB=60 e avremmo avuto una migliore approssimazione. Resta comunque il fatto che il sistema decimale offre sempre risultati approssimati. |
|||||||||||||||
|
Risolviamo con Geogebra il problema posto da Fibonacci: si tratta di dividere 100 lire in tre parti proporzionali a 17, 19 e 42. Aumentiamo il numero di cifre decimali a 4 e prendiamo AB = 10
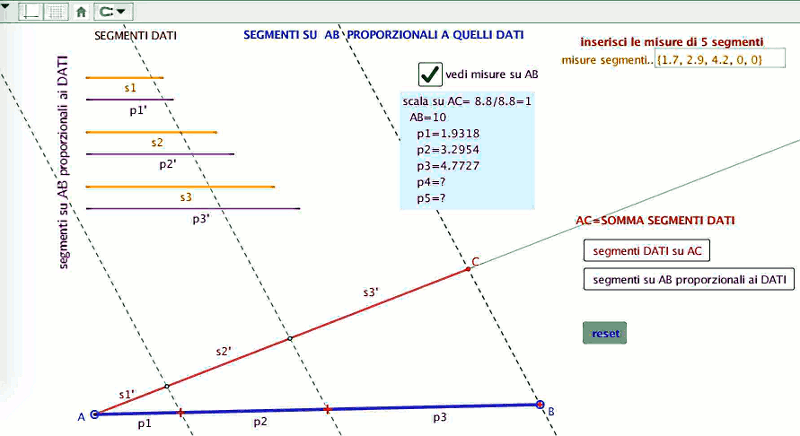
Troviamo, moltiplicando per 10 i risultati forniti da Geogebra, p1= 19.31 , p2= 32.95 , p3= 47,72 la somma di questi valori è 99,98 minore di 100 di 120. Ora 150 di una lira è poco meno di 5 denari restano dunque 5 denari indivisi. Il calcolo di Fibonacci fornisce i valori esatti divisi in lire soldi ( 120 di una lira) e denari ( 112 di un soldo): per il primo socio 19+620+420×12+420×12×11, cioè 19 lire, 6 soldi, 4 denari e 411 di un denaro; per il secondo socio 32+120+120×12+1920×12×11 e per il terzo 47+620+620×12+1420×12×11. Il confronto tra il sistema decimale e l’aritmetica delle frazioni in questo esempio evidenzia la differenza tra un calcolo esatto e un calcolo approssimato.
Lasciamo per esercizio il problema, proposto da Calandri, di dividere tra i tre ladri i “1000 fiorini larghi” usando sia metodi aritmetici che metodi geometrici e confrontando le soluzioni trovate. Anche il fiorino è diviso in soldi (
120 di un fiorino) e denari (
112 di un soldo)
|
|||||||||||||||
|
Concludiamo con un celebre enigma:

Un visir morendo lasciò ai suoi tre figli 17 cammelli in eredità e ordinò che la metà di essi fosse data al primo figlio, la terza parte al secondo e la nona parte al terzo. I tre figli cominciarono a litigare tra loro perché il più grande pretendeva 9 cammelli mentre gli altri sostenevano che non ne avesse diritto. Si rivolsero allora, per la divisione, a un Matematico, il quale venne col proprio cammello che unì agli altri. Diede la metà dei 18 cammelli, cioè 9 al primo, un terzo cioè 6 al secondo e un nono cioè 2 al terzo, e poi, ripreso il suo cammello se ne andò ringraziato dai tre figli, ognuno soddisfatto di tale divisione.
Lo studente esperto in aritmetica può ora, a ragione, considerarsi un solutore di controversie! |
|||||||||||||||