progetto fibonacci - traduzione-09_parte

parte terza cap IX

Parte Terza

Finisce la parte seconda del nono capitolo.
Inizia la terza sui cavalli che mangiano orzo nei giorni proposti.

La geometria
del baratto:
la figura cata

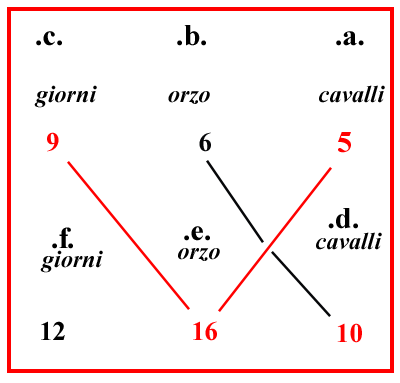
(IX.3.1 ; G: IX.127) C

inque cavalli mangiano 6 sestari di orzo in 9 giorni; si chiede in quanti giorni, nel medesimo modo, dieci cavalli mangeranno 16 sestari: poni sulla linea superiore 5 per i cavalli, e 6 per l'orzo, e 9 per i giorni, scrivendo naturalmente all'indietro [ da destra a sinistra ]; e sotto il 5 porrai 10 cavalli, e sotto il 6 poni 16 sestari; e moltiplica il 5 per 16; e per 9, farà 720; dividilo per 6, e per 10, farà 12 giorni: o altrimenti, poiché 5 cavalli mangiano 6 sestari in 9 giorni; dunque 10 cavalli mangeranno il doppio dei 6 sestari in altrettanti giorni, poiché 10 cavalli sono il doppio di 5 cavalli. E ancora, poiché 10 cavalli mangiano 12 sestari in 9 giorni; dunque essi mangeranno 16 sestari in 12 giorni che risulta dalla moltiplicazione di 16 per 9 divisa per 12.

5 6 = 10 12	12 9 = 16 x
5 6 × 16 x = 10 9

(IX.3.2 ; G: IX.129) P

ossiamo allora mostrare in questa questione 18 combinazioni di proporzioni che si mostrano in sei linee nella figura cata. Sia così un numero .e. sulla prima linea, e .f. sulla seconda, e .d. sia sulla terza, e .a. sia sulla quarta, e .b. sulla quinta, e un numero .c. sia sulla sesta linea; e il numero .a.e.c. sia una certa unione, che sarà chiamata la prima: mentre il numero .d.b.f. sia la seconda unione. Inoltre la proporzione di ciascun numero della prima unione a ciascun numero della seconda è composta dai quattro numeri restanti; e due di essi sono antecedenti e due conseguenti. Perciò ciascuna proporzione di quelle proporzioni composte, che sono 9, si compone secondo una combinazione di proporzioni: perché quando una certa proporzione è composta dal primo antecedente, e dal primo conseguente, e dal secondo antecedente, e dal secondo conseguente, si comporrà anche la stessa proporzione in cambio, che ha il primo antecedente al secondo conseguente; e dalla proporzione, che ha il secondo antecedente conseguente al primo. Infatti non sono mutati i prodotti fatti dagli antecedenti, né dai conseguenti; poiché gli stessi numeri prodotti fanno una proporzione composta, che si compone dei due antecedenti e dei due predetti conseguenti.

Figura cata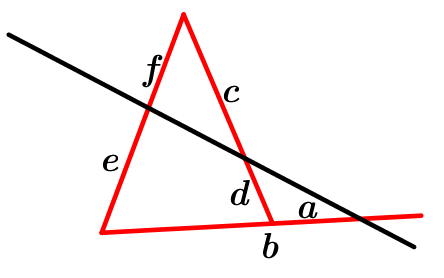

Teorema di Menelao piano

c =

b ×

pg.133

(IX.3.3 ; G: IX.131) S

imilmente la proporzione di ciascun numero della seconda unione a ciascun numero della prima è composta dai quattro restanti numeri, dei quali due sono antecedenti e due conseguenti. Per cui si formano altre 9 combinazioni. E noi mostriamo che la composizione della proporzione del primo numero .e. al secondo .f. è composta dai quattro numeri restanti; dei quali i numeri .d. .b. sono antecedenti; e i restanti .a. .c. sono conseguenti; questo sarà così provato: poiché dalla moltiplicazione del numero .e. per quello fatto da .a. .c. , cioè per 16 e poi per 9, e poi per 5, diviso per il numero fatto dai numeri .d. .b. si ha il numero .f. . Quindi se si moltiplica il numero fatto dai numeri .d. .b. per .f. sarà uguale alla moltiplicazione di .e. per il numero fatto dai numeri .a. .c. , perciò proporzionalmente come il numero fatto dai numeri .d. .b. sta al numero fatto dai numeri .a. .c. così .e. sta ad .f. quindi i numeri .d. .b. , come ho detto, sono antecedenti, e .a. .c. sono conseguenti. Quindi la proporzione di .e. ad .f. è composta dalla proporzione dell'antecedente .d. al conseguente .a. e dalla proporzione del similmente antecedente .b. al conseguente .c. ; come la proporzione di .e. ad .f. si compone dalle proporzioni permutate, cioè da quella fra il numero .d. e il numero .c. , e da quella fra .b. ed .a. ; mostrerò tutto questo anche in un altro modo, con i numeri.

f =

d×b

a×c

a×

c×

(IX.3.4 ; G: IX.134) P

oiché come il 10 sta al 5, cioè come il numero .d. sta al numero .a. , così quello fatto dai numeri .b. .d. sta a quello fatto dai numeri .b. .a. ; cioè come 10 cavalli stanno a 5 cavalli, così 60 cavalli stanno a 30 cavalli; e così, come 60 cavalli stanno a 30 cavalli, così 60 sestari stanno a 30. E ancora, come 6 sestari stanno a 9 giorni, cioè come .b. sta a .c. , così il numero fatto dai numeri .a. .b. sta al numero fatto dai numeri .a. .c. ; cioè come 6 sestari stanno a 9 giorni, così 30 sestari stanno a 45 giorni: dunque come .d. sta ad .a. così i 60 sestari stanno ai 30 sestari e come .b. sta ad .c. così i 30 sestari stanno ai 45 giorni: dunque la proporzione dell'orzo ai giorni è come quella di 60 a 45, la cui proporzione si è mostrato essere composta da quella da .d. ad .a. e da .b. a .c. : quindi come 60 sestari stanno a 45 giorni, così 16 sestari stanno ai giorni richiesti, cioè il numero .e. sta al numero .f. ; e così la proporzione di .c. con .f. si è mostrato di essere composta da quella da .d. ad .a. e da .b. a .c. , come occorre.

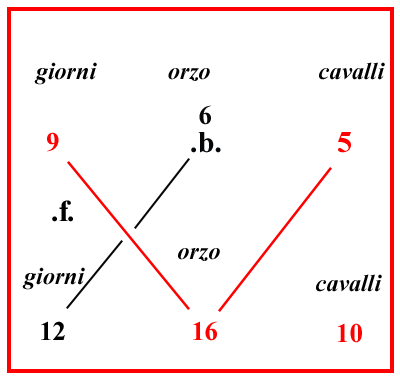
(IX.3.5 ; G: IX.136) S

imilmente mostrerò che la proporzione di .e. ad .f. è composta da quella da .d. a .c. e da quella da .b. ad .a. ; e così abbiamo una combinazione. Similmente si può mostrare che la proporzione di .c. ad .f. è composta dai quattro numeri rimanenti. Dei quali, ancora, i numeri .d. e .b. sono antecedenti, e invece gli altri .e. .a. , sono conseguenti; e la moltiplicazione del numero fatto dai numeri .a. ed .e. per il numero .c. , cioè 720, è uguale alla moltiplicazione del numero fatto dagli antecedenti .d. e .b. per il numero .f. ; e così si ha la seconda combinazione. Allo stesso modo si mostrerà che .a. che resta dalla prima unione, è composta ad .f. dai quattro numeri restanti; dei quali, ancora, i numeri .d. e .b. sono antecedenti e gli altri, cioè .e. e .c. sono conseguenti; e così si ha la terza combinazione. E così si è mostrato che la proporzione di ciascuno dei tre numeri della prima unione al numero .f. , che è uno dei tre numeri della seconda unione, è composta dalle due proporzioni dei restanti quattro numeri. E ancora, nel suddetto modo, si chieda, quanti cavalli mangino 16 sestari in 12 giorni: scrivi nel riquadro orzo sotto orzo, e giorni sotto giorni, e dividi il numero fatto dai tre numeri della prima unione, cioè 720, per gli altri due numeri, cioè per 12, e per 6, farà 10 per i cavalli richiesti. Inoltre in questo problema si può mostrare, col modo suddetto, che la proporzione che ha ciascun numero della prima unione al 10, che è un altro numero della seconda, si compone delle due proporzioni fra gli altri quattro numeri, dei quali gli antecedenti sono 12 a 6, cioè i numeri .f. e .b. ; e così si hanno altre tre combinazioni in questo riquadro.

f =

d×b

e×a

f =

d×b

e×c

pg.134

(IX.3.6 ; G: IX.140) E si dica che 10 cavalli mangino 16 sestari in 12 giorni; e si chieda quanti sestari mangeranno 5 cavalli in 9 giorni; adesso in questo riquadro manca il terzo numero della seconda unione, perciò i restanti due numeri di medesima unione, cioè 10 e 12, saranno i divisori; per i quali dividerai il 720, che è generato da 5 per 16 per 9, farà 6 sestari di orzo, come si mostra in questa terza figura; nella quale si può capire perfettamente che la proporzione di ciascun numero della prima combinazione al 6, che è il terzo dei numeri della seconda combinazione, è composta dalle due proporzioni dei quattro numeri restanti, fra i quali gli antecedenti sono il 10 e il 12; gli altri due sono i conseguenti. e così si ottengono nove combinazioni. E troverai le altre 9 combinazioni dalla composizione della proporzione di ciascuno dei tre numeri della seconda unione a ciascuno dei tre numeri della prima: e queste composizioni sono fatte dalle due proporzioni, che si fanno fra gli altri quattro numeri, dei quali in ciascuna combinazione ci saranno sempre due antecedenti dai numeri della prima unione. E si deve notare, che nessuno dei suddetti sei numeri ha una proporzione composta verso qualche numero della sua unione fra le due proporzioni rimanenti, e queste proporzioni sono dodici.

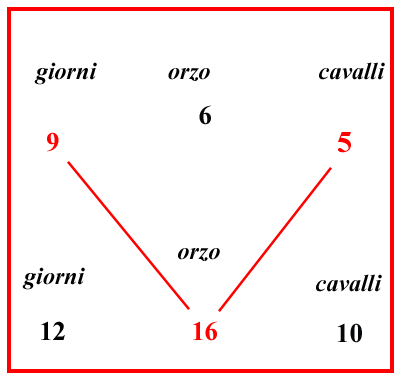
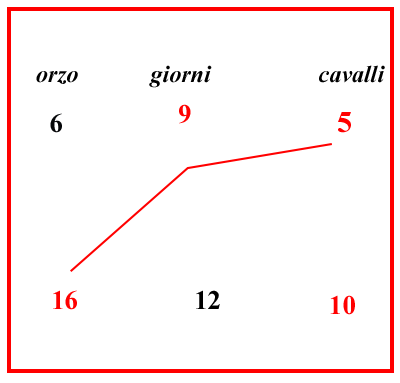
(IX.3.7 ; G: IX.143) E se negli schemi suddetti si ponessero i giorni in mezzo ai cavalli e all'orzo, come si vede in quest'altro riquadro; allora i numeri della prima unione saranno 5, e 9, e 16; gli altri sarebbero i numeri della seconda unione; che saprai così: si ponga che sia ignoto un numero della linea inferiore; e poiché 5 cavalli mangiano una certa misura data di orzo, cioè 6 sestari in giorni dati, cioè in 9; quindi 10 cavalli mangeranno altrettanto orzo in

4 giorni, che provengono dalla moltiplicazione di 5 per 9, divisa per 10. E ancora, poiché in

4 giorni 10 cavalli mangeranno 6 sestari; si chiede quanti sestari mangeranno in 12 giorni: quindi come

4 sta a 6, così 12 sta alla quantità richiesta d'orzo. Perciò sono da moltiplicare 12 per 6, e da dividere per

4; perché come un numero sta a un numero, così il decuplo dell'uno sta al decuplo dell'altro. Se di conseguenza avremo moltiplicato per 10 la moltiplicazione di 12 per 6, cioè moltiplicheremo 10 per 12, e per 6; e avremo diviso il totale, che è 720, per il decuplo di

4, cioè per 5 e per 9, che sono nella linea superiore, farà 16 per la quantità ignota di orzo: perciò se moltiplicheremo 5 per 9 e per 16, si sarà reso uguale alla moltiplicazione di 10 per 12 per 6; e così il 5 e il 9 e il 16 fanno la prima unione. I rimanenti, cioè il 10 e il 12 e il 6, fanno invece la seconda. Per cui quando qualcuno dei predetti sei numeri che avrai voluto ricavare sarà stato ignoto, guarda da quale numero sarà stato in unione; perché dividerai per gli altri due numeri della sua unione il numero fatto dai tre numeri della restante unione, e avrai il numero cercato.

Sugli uomini che piantano alberi in un numero di giorni stabilito.

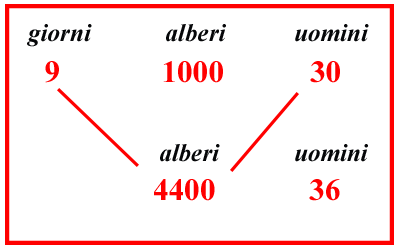
(IX.3.8 ; G: IX.146) I

n una pianura un certo re inviò 30 uomini per piantare degli alberi in essa; questi piantarono là 1000 alberi in 9 giorni; e si chiede in quanti giorni 36 uomini piantarono 4400 alberi: se invero riportati 36 uomini sotto 30, e 4400 alberi sotto 1000 alberi, come si vede in questo riquadro, moltiplicherai 30 uomini per 4400 alberi e il loro prodotto per i 9 giorni, e dividerai tutto il risultato per 36 uomini e per i 1000 alberi; farà 33, e in così tanti giorni gli stessi uomini pianteranno i 4400 alberi.

Sullo stesso

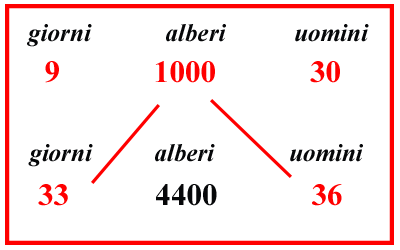
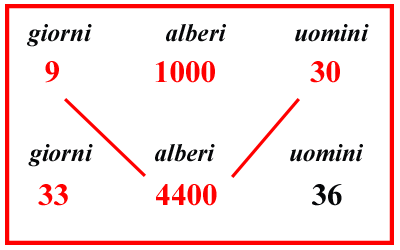
(IX.3.9 ; G: IX.147) E ancora se invece si chieda nel modo soprascritto di 36 uomini quanti alberi piantarono in 33 giorni; scritto il problema, come qui si mostra, moltiplicherai 36 uomini, e 1000 alberi, e 33 giorni solo in una volta e dividerai, per 30 uomini e 9 giorni, farà 4400 alberi.
Ugualmente se, nello stesso modo, si chieda quanti uomini piantarono 4400 alberi in 33 giorni, scriverai il problema come qui si mostra, e moltiplicherai 30 uomini, e 4400 alberi, e 9 giorni in una sola volta, e dividerai il prodotto per 1000 e per 33, farà 36 uomini, come è necessario.

Sugli uomini che mangiano frumento.

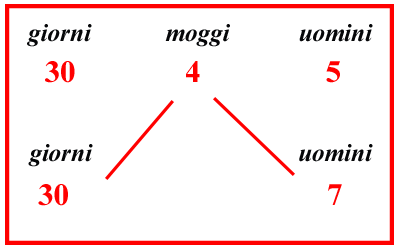
(IX.3.10 ; G: IX.149) C

inque uomini mangiano 4 moggi di frumento in un solo mese, cioè in 30 giorni. Per cui altri sette uomini cercano di sapere, quanti moggi loro siano sufficienti, nello stesso modo, nei medesimi 30 giorni: se invero scriverai la questione come si mostra qui, e moltiplicherai 7 uomini per 4 moggi, e per 30 giorni, che sono sula linea inferiore, e dividerai il risultato per 5 uomini, e per 30 giorni, che sono sulla linea superiore. Quindi non moltiplicherai per 30 né dividerai per 30: quindi moltiplicherai solo 7 per 4, e dividerai per 5, farà

5 moggi. E sappi perché abbiamo proposto questo problema; perché da ciò anche riguardo al vino che si beve spesso sorge una disputa tra i mercanti; perciò ricordala bene a memoria perché tu sappia operare in simili questioni.

Termina la terza parte del nono capitolo.

Termina il nono capitolo.