Fibonacci e i rotti
un approccio
storico e laboratoriale
allo studio delle frazioni
Diario di bordo
classe 2H dell’IC Piazza Winckelmann - Roma a.s. 2019-20
Questo lavoro, che si configura come un laboratorio di matematica, nasce dal desiderio di rendere più accessibile uno dei nodi della programmazione della matematica nella scuola secondaria di primo grado: le frazioni. Attraverso la lettura del Liber abaci di Leonardo Fibonacci tentiamo un approccio storico allo studio del concetto di frazione come numero. Attraverso specifiche attività didattiche vorremmo mettere in evidenza il grande contributo reso da Fibonacci allo sviluppo della scienza italiana ed europea con la diffusione della cultura indo araba:
queste sono alcune delle domande a cui proveremo a dare risposte partendo da osservazioni condivise frutto di attività svolte in classe.
Dal link https://www.progettofibonacci.it/liber/BONCOMPAGNI/trad/trad05B.html abbiamo letto in classe la prima pagina del capitolo V del Liber abaci in cui Fibonacci spiega per la prima volta come deve essere scritta una frazione.
Il laboratorio è iniziato nel mese di ottobre 2019 ed è terminato alla fine di dicembre.
Metodologia
Abbiamo cercato di lavorare nel giorno della settimana in cui l’orario prevede due ore consecutive: il lavoro con le mani , ma soprattutto la fase di discussione e condivisione richiedono tempo e calma.
La classe lavora divisa in 5 gruppi da 4 o 5 (22 alunni):
Gruppo 1 (G1): Guido, Emma, Giorgia, Edoardo |
Gruppo 2 (G2): Matteo Galassi, Ludovica, Matteo Cabiddu, Ginevra, Matilde |
Gruppo 3 (G3): Lucia, Simone Saccone, Giulio Sisti, Arianna |
Gruppo 4 (G4): Chiara , Daniele, Angelica C, Gabriel, Giovanni |
Gruppo 5 (G5): Giulia, Ludovico, Ivan, Angelica D. |
Durante le attività l’insegnante svolge un ruolo di supervisione, raccogliendo una documentazione fotografica e in fase di condivisione delle osservazioni modera gli interventi.
Vogliamo arricchire con i ragazzi ogni 7 giorni il diario di bordo riportando le osservazioni fatte in classe e descrivendo con le nostre parole quanto fatto.
Al termine di ogni settimana l’insegnante divide in segmenti le attività svolte e affida la verbalizzazione di ciascuna attività a un gruppo secondo un format comune. Nell’incontro successivo viene condivisa la lettura del diario, suggerendo se necessario integrazioni e/o modifiche.
Premessa
Abbiamo conosciuto Leonardo Fibonacci: chi era, quando è vissuto, perché è venuto in contatto con la ricca cultura araba ed ha intuito i grandi vantaggi che sarebbero venuti dall’uso del nuovo sistema di numerazione. Il contesto storico è quello della fiorente espansione della Repubblica marinara di Pisa che estende i suoi commerci in tutto il Mediterraneo. Il giovane Leonardo raggiunge il padre in Tunisia dove completa la sua istruzione venendo a conoscere la matematica araba. Capisce l’enorme ricchezza del nuovo sistema di numerazione e , non senza difficoltà, comincia a diffondere la nuova scuola il Italia.
La prima attività svolta è stata la costruzione del materiale da usare con le mani.
Siamo partiti da questa scheda stampata in dimensione A4
come prima cosa abbiamo osservato cha la stessa asta (rettangolo) viene divisa in parti uguali sempre più piccole: nella seconda riga due parti uguali, nella terza tre e così via fino a 12: ognuna delle parti in cui è divisa l’unità è l’unità frazionaria.
Abbiamo quindi completato la scheda scrivendo in ciascuna parte l’unità frazionaria corrispondente
A questo punto abbiamo incollato la scheda su un cartoncino e abbiamo tagliato prima le strisce e poi le singole unità frazionarie avendo cura di separare, usando dei sacchettini o una scatola a scomparti, i diversi gruppi di unità frazionarie.
Gruppo 5 (G5): Giulia, Ludovico, Ivan, Angelica D
Materiale usato: per costruire un numero rotto abbiamo utilizzato un intero e l’abbiamo diviso in parti uguali.
Esempi svolti in classe: costruiamo 6/7
spiegate che cos’è un numero “rotto” per Fibonacci:
per Fibonacci un numero rotto è una parte dell’intero che è stato diviso in parti uguali.
un rotto si scrive usando due numeri interi separati da una linea orizzontale
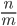
m il numero che si trova sotto la linea orizzontale rappresenta le parti in cui è diviso l’intero e si chiama denominatore
n il numero che si trova sopra la linea orizzontale rappresenta le parti prese in considerazione e si chiama numeratore
Un rotto ha il numeratore minore del denominatore.
regola generale: come costruire un rotto tipo
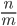con n<m
Si sommano tante unità frazionarie (denominatore =m) quante indicate dal numeratore n
Gruppo 2 (G2): Matteo Galassi, Ludovica, Matteo Cabiddu, Ginevra, Matilde
Materiale usato: unità frazionarie costruite con la carta e plastificate
esempi svolti in classe: costruiamo 7/4 cioè 1 ¾
spiegate che cos’è un numero “misto” per Fibonacci e quale notazione viene usata per scriverli:
Per Fibonacci un numero misto è dato dalla somma di un intero con un numero rotto che deve avere il numeratore minore del denominatore.
Regola generale: come costruire un numero misto tipo
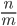con n>m
Gruppo 1 (G1): Guido, Emma, Giorgia, Edoardo
Materiale usato: Unità frazionarie o rotti di diverse misure.
Esempi svolti: sono state prese diverse unità frazionarie o rotti e sono state confrontate tra loro.
Spieghiamo come abbiamo lavorato con le aste: (Edoardo)
Regola generale: I rotti sono disposti uno sotto l’altro con un estremo allineato; dall’immagine si può vedere che ⅖ sono più grandi di ⅓
nella foto 2/10 < 4/10
nella foto 4/6 < 4/10
per il momento osserviamo con attenzione la costruzione allineando bene i due rotti da confrontare ad un estremo
¼ < 4/10
Gruppo 4 (G4): Chiara , Daniele, Angelica C, Gabriel, Giovanni
per fare questa attività ciascuno deve integrare il materiale e costruire almeno tre aste corrispondenti all’intero (1/1). Bisogna formare i numeri misti come somma di interi e rotti seguendo il procedimento dell’attività della costruzione di misti
Materiale usato: Aste frazionarie di valori diversi.
esempi svolti: Sono stati confrontati due rotti di diverse misure 7/6 e 12/9
regola generale: come confrontare due numeri misti qualsiasi?
Se i misti hanno la stessa parte intera; è maggiore quello con la parte frazionaria maggiore nell’immagine, cioè con il rotto maggiore
Invece i misti con la diversa parte intera è maggiore quello con la parte intera maggiore.
Esempio: 2 ⅓ > 1 ⅘
Infine i misti sono uguali quando la parte intera e i rotti sono uguali.
Gruppo 3 (G3): Lucia, Simone Saccone, Giulio Sisti, Arianna
Materiale usato: Abbiamo usato delle aste divise in parti diverse che però hanno lo stesso valore.
introduzione
Esempio: scrivere 1/3 con rotti con altri denominatori
1/3 = (1/6 + 1/6) =2/6
L’asta 1/3 è lunga come due aste da 1/6
esempi svolti in classe:
½= (¼ + ¼) = ⅙ + ⅙ + ⅙ = 1/12 +1/12 +1/12 +1/12 +1/12 +1/12 = ⅛ +⅛ +⅛ +⅛ =1/10 +1/10 +1/10 +1/10 +1/10 +1/10
⅔ =⅙ +⅙ +⅙ +⅙ = 1/12 +1/12 +1/12 +1/12 +1/12 +1/12 +1/12 +1/12
In classe ogni gruppo ha proposto le seguenti regole:
G3: moltiplicando sia il numeratore che il denominatore della frazione primaria per lo stesso numero ottengo una frazione che indica la stessa quantità
G2: possiamo trovare i rotti “equivalenti” , cioè che indicano la stessa quantità , solo con i multipli secondo lo stesso numero del numeratore e del denominatore
G4 : il rotto può essere espresso in modo diverso usando i divisori o i multipli del denominatore e dividendo o moltiplicando il numeratore per lo stesso numero
G5 bisogna moltiplicare numeratore e denominatore per lo stesso numero intero
G1: Dividendo più volte per per un divisore comune a numeratore e a denominatore, sia il numeratore che il denominatore, si tornerà sempre al rotto che ha numeratori e denominstore più piccoli
Regola per rappresentare un rotto come somma di rotti con un altro denominatore (oggi diciamo come costruire frazioni equivalenti ad una frazione data
Per costruire una frazione equivalente ad una frazione già data,dobbiamo moltiplicare numeratore e denominatore per uno stesso numero diverso da zero o dividere per per un divisore comune a numeratore e a denominatore, sia il numeratore che il denominatore
A che serve rappresentare un rotto in tanti modi diversi?
all’inizio può sembrare una complicazione…….
Come si possono sommare due rotti? Ci verrà in aiuto l’esercizio appena fatto …. l’unica difficoltà sarà saper scegliere quale sarà la rappresentazione adatta per poter calcolare la somma fra rotti
Vediamo degli esempi:
Ad ogni gruppo viene assegnata una tabella di addizioni tratte dal Liber abaci: i gruppi di suddividono in coppie e cominciano a costruire le somme con l’aiuto del materiale, trovando ogni volta la rappresentazione adatta.
Il lavoro continua a casa per tutti perchè non si riesce in un’ora a eseguire le somme.
Al termine del laboratorio, dopo aver costruito molte somme con il materiale, ogni gruppo deve scrivere la
Regola per sommare due rotti:
G1 - REGOLA PER SOMMARE DUE ROTTI
caso 1: addizioni fra rotti con lo stesso denominatore
per ottenere la somma di due frazioni con lo stesso denominatore basta addizionare i numeratori.
caso 2: addizioni fra rotti con denominatore diverso:
per ottenere la somma di due frazioni con diverso denominatore bisogna trovare il m. c. m. dei denominatori, moltiplicare i numeratori per lo stesso numero (è il numero che si ottiene dividendo il nuovo denominatore per il vecchio) e poi sommare i numeratori.
G2 - REGOLA PER SOMMARE DUE ROTTI
Per addizionare 2 rotti che hanno denominatore uguali basta addizionare i numeratori
Per addizionare 2 o più frazioni con denominatore diverso bisogna:
G3 - REGOLA PER SOMMARE DUE ROTTI
G4 - REGOLA PER SOMMARE DUE ROTTI
G5 - REGOLA PER SOMMARE DUE ROTTI
Dopo aver ascoltato tutte le proposte, cegliamo la formulazione del Gruppo 2 G2
G2 - REGOLA PER SOMMARE DUE ROTTI
Per addizionare 2 rotti che hanno denominatore uguali basta addizionare i numeratori
Per lunedì 4 novembre
Cerchiamo di spiegare in dettaglio il punto b) del caso 2 rispondendo alla seguente domanda:
“una volta stabilito il nuovo denominatore comune a tutti rotti da sommare, come si trasformano i numeratori?
G1: per trasformare tutti i rotti devo dividere il m .c.m per il denominatore e moltiplicarlo per il numeratore .
G2: abbiamo diviso il m .c.m per il denominatore e moltiplicato per il numeratore
G3: Si divide m .c.m per il primo denominatore e lo si moltiplica per il suo numeratore . infine si sommano i due rotti.
G4: Il numeratore dev’essere moltiplicato per il risultato della divisione fra l’ m .c.m e il vecchio denominatore.
G5: dopo aver trovato il m .c.m. per trovare il numeratore si deve dividere il m .c.m per il primo denominatore e poi moltiplicarlo per il numeratore
Esempio
Come prima cosa scriviamo gli addendi come numeri misti, aiutandoci con le aste
L’addizione diventa
Possiamo perciò sommare interi con interi e rotti con rotti secondo le regole che già conosciamo
Ad ogni gruppo si consegna un’addizione fra misti da calcolare utilizzando le aste
… e alla fine con il contributodi tutti i gruppi, costruiamo un grande manifesto che contiene tante addizioni rotti, come faceva Fibonacci per aiutare i suoi alunni a ricordare il metodo per la somma di rotti (abbiamo usato carta pergamena e abbiamo bruciato i bordi della carta da pacco per anticarla)
Proviamo
Come per l’addizione dobbiamo esprimere i rotti con rotti equivalenti che abbiano le stesso denominatore
Ma in questo caso faremo la sottrazione dei numeratori
Il risultato della sottrazione è il rotto che manca a ⅓ per diventare lungo come 1/2
Con l’aiuto delle aste calcoliamo altre sottrazioni fra rotti e cerchiamo di verbalizzare il procedimento.
Per visualizzare la sottrazione fra rotti usando le aste queste devono essere posizionate in modo differente rispetto alla somma: spiega la differenza
G2: La differenza fra rotti con le aste si può trovare sistemando i rotti uno sotto l’altro in modo che abbiano un estremo allineato e guardando lo spazio mancante (quanto manca al più piccolo per diventare lungo come il grande?) per esempio:
5/3-1/3=4/3
4/3 è la differenza
Spiega la regola generale per eseguire la differenza fra rotti:
G1: devo trovare m
.c.m tra denominatori poi dividerlo per il denominatore moltiplicare per il numeratore e sottrarre per ottenere la differenza; lavorando con le aste bisogna metterel una sotto l’altra in modo che un estremo sia allineato.
G3: Quando si hanno i denominatori uguali si eseguono i calcoli della sottrazione solo tra i numeratori. Quando invece si hanno i denominatori diversi si calcola il m
.c.m tra i denominatori, si trasformano le frazioni come nel caso delle addizioni e poi si eseguono i calcoli.
G4: Nel primo caso quando i rotti hanno un denominatore in comune bisogna eseguire la sottrazione tra i numeratori.
Nel secondo caso, invece, quando i denominatori sono diversi, per primo bisogna trovare il m
.c.m in comune, poi trasformare i rotti come nell’addizione e poi eseguire la sottrazione.
G5: Quando si hanno i denominatori uguali basta sottrarre i numeratori dei due termini e il denominatore rimane lo stesso.
Quando invece abbiamo due denominatori diversi troviamo il m
.c.m. tra di loro e poi lo dividiamo per il denominatore del primo termine e poi il risultato lo moltiplichiamo per il numeratore. Si replica questo passaggio anche per l’altro termine e poi si sottraggono i numeratori.
In questa parte del laboratorio oltre alle aste usiamo anche fogli di carta bianca A4, una squadra grande e matite colorate
Cerchiamo di rappresentare geometricamente questa operazione ricordando che il prodotto è rappresentato a × b dall’area del rettangolo
Prendiamo un foglio A4 e disegniamo un quadrato di lato 1/1 usando come unità l’asta 1/1;
|
|
Vogliamo rappresentare la moltiplicazione ¾ × 2/3 e prendiamo dalla nostra scatola il materiale opportuno;
|
|
|
|
Mettiamo in evidenza il rettangolo di lati ⅔ e ¾ (l’immagine seguente è ottenuta con geogebra)
Per casa viene affidata la realizzazione di un’altra moltiplicazione con la stessa costruzione geometrica:
eseguire su un foglio bianco con le aste la moltiplicazione 1/2 × 3/5
La regola appare subito anche dopo la prima costruzione fatta in classe: il rotto che rappresenta il prodotto si ottiene moltiplicando numeratore per numeratore e denominatore per denominatore.
La verifichiamo con altri esempi.
Un’altra osservazione: moltiplicando due rotti si ottiene un rotto; otteniamo infatti un rettangolo che occupa solo una parte del quadrato unitario.
ecco un esempio del compito svolto a casa
Seguiremo sempre la costruzione geometrica della moltiplicazione , cioè costruiremo il rettangolo che ha come dimensioni i due fattori; vista la grandezza dei numeri avremo bisogno della carta A3
Vogliamo costruire geometricamente il prodotto:
1 2/7 × 1 1/5
tracciamo la prima dimensione mettendo sulla riga le aste che rappresentano il numero misto1 2/7; ricordiamoci di mettere una tacca in corrispondenza alla lunghezza delle unità frazionarie
|
Tracciamo la dimensione perpendicolare aiutandoci con la squadra e mettendo su di essa le aste corrispondenti al secondo fattore; ricordiamoci di mettere una tacca in corrispondenza alla lunghezza delle unità frazionarie
|
|
Il rettangolo complessivo che indica il prodotto viene così ad essere diviso in diverse parti |
|
|
|
|
per casa viene chiesto di realizzare un’altra moltiplicazione fra misti sull’altra facciata del foglio A3
(1+⅖) × (1+⅓)
ecco uno dei lavori dei ragazzi
per questa parte del laboratorio abbiamo usato il seguente materiale:
|
Cominciamo con la divisione di un rotto per un intero
esempio: ½ : 3
prendiamo l’asta di carta corrispondente a ½ , lo pieghiamo in 3 parti uguali e troviamo nella scheda generale il rotto corrispondente, cioè ⅙
per risolvere questi casi ricordiamo il concetto di divisione come contenenza:
Ci chiediamo: quante aste da ⅛ sono contenute in ½? proviamo a risolvere il quesito usando le aste
Risolviamo cioè la divisione
1/2 : 1/8 = 4
Procediamo con molti esempi differenti sia per la divisione di rotti per interi e sia nella divisione fra rotti;
⅓ : 1/12 = 4
⅓ × 12 =4
|
Abbiamo visto che la moltiplicazione a × b corrisponde geometricamente all’ area A del rettangolo che ha le dimensioni a e b. Sappiamo già dalla scuola primaria che la divisione è l’operazione inversa della moltiplicazione ; proviamo quindi un approccio geometrico. Cominciamo da casi semplici usando numeri interi e la carta a quadretti. |
Problema: Conosciamo l’area di un rettangolo pari a 8 u2. Vogliamo sapere qual’ è la misura dell’altezza h del rettangolo di area A = 8 u2 e base b =4u.
Risolviamo il problema geometricamente:
Possiamo verificare che l’area del nuovo rettangolo verde di dimensioni 4u e 2u ha area 8 u2 sia applicando la formula della moltiplicazione sia contando i quadretti contenuti all’interno del rettangolo.
Abbiamo trovato geometricamente che
h= A : b = 8 : 4 = 2u
Ecco un altro esempio fatto in classe sempre con i numeri interi:
Con la carta a quadretti è facile verificare che le aree dei due rettangoli sono uguali, perchè come abbiamo visto basta contare i quadretti. proviamo però a dimostrarlo più in generale:
Il rettangolo grande AIFH è diviso dalla diagonale HI in due triangoli rettangoli HIF e HAI uguali perchè i lati che formano l’angolo retto sono le dimensioni del rettangolo e il terzo lato è la diagonale che è in comune;
La descrizione delle figure deve essere generale senza le misure
Il triangolo HIF è costituito da tre figure: descrivile (G1):le tre figure sono:
Il triangolo HGC è uguale al triangolo HDC perchè (G3) la diagonale HC del rettangolo HDCG divide il rettangolo in due triangoli uguali.
Il triangolo BCI è uguale al triangolo CEI perchè (G4) perchè il rettangolo è stato diviso da una diagonale in due parti uguali .
Vogliamo dimostrare che i due rettangoli piccoli che abbiamo costruito sono uguali perchè possono essere ottenuti come differenza di figure che hanno la stessa area.
Vediamo un esempio in cui si dimostra l’equivalenza di due figure non uguali sottraendo alla stessa figura di partenza a parti uguali
Possiamo concludere che se ad aree uguali togliamo parti di area uguale le parti rimanenti avranno l’area uguale fra loro.
Nel nostro caso il rettangolo verde sarà equivalente a quello rosso perchè dai due triangoli rettangoli grandi HIF e HAI abbiamo tolto parti uguali (parti in grigio).
Usando il metodo precedente proviamo ad operare una divisione fra rotti; per questo procedimento abbiamo bisogno di:
partiamo dal seguente problema:
Trova l’altezza del triangolo di area ⅛ e base ½
Ad ogni foto va inserita la didascalia spiegando il procedimento:
(scrivo la prima per le altre indico il gruppo che deve completare)
Cominciamo con la costruzione del rettangolo di base 1/1 e altezza ⅛ che avrà area ⅛ come richiesto dal problema
Sul foglio A3 con l’aiuto della squadra tracciamo la base del rettangolo con l’aiuto dell’asta 1/1
G5 Per costruire l’altezza dobbiamo prendere la squadra e disegnare un segmento pari a ⅛
G1: sempre aiutandoci con la squadra e la riga disegnamo l`altra altezza di ⅛
G2:prolunghiamo una base del segmento aiutandoci con un asta
G3: Dopo aver rappresentato il rettangolo più semplice di area ⅛ che ha come dimensioni ⅛ e 1, abbiamo attaccato al rettangolo la misura delle base richiesta per i nuovo rettangolo.
G4:Tracciamo una linea che passa per l’estremo in basso a sinistra e per l’estremo in alto a destra del rettangolo di partenza fino ad incontrare la verticale che prolunga il lato sinistro del primo rettangolo: il punto di intersezione indica l’altezza richiesta per il secondo rettangolo
G5 infine traccio una linea parallela alla base del primo rettangolo dal punto che ho trovato prima fino all’ultimo segmento (aiutandomi sempre con la squadra)
G1:ora verifico a quale frazione corrisponde l’altezza trovata in precedenza
Dopo aver trovato il valore della seconda dimensione del rettangolo proviamo a calcolare l’area :
b × h= ½ × ¼ = ⅛
Proviamo a calcolare la misura dell’altezza con il procedimento aritmetico
Scriviamo quindi nuovamente la regola per dividere due frazioni:
G1: in tutte le divisioni tra frazioni si arriva al risultato invertendo il denominatore e il numeratore della seconda frazione e sostituendo il diviso con il simbolo ×
G2: nelle divisioni tra frazioni solo per la seconda frazione si inverte il denominatore con il numeratore si sostituisce il÷con il× poi si calcola come una moltiplicazione
G3: per eseguire una divisione tra due rotti bisogna, solo relativamente alla seconda frazione, scambiare il denominatore con il numeratore e poi svolgere una normale moltiplicazione.
G4: Per svolgere la divisione bisogna invertire il denominatore con il numeratore del secondo rotto ed eseguire la moltiplicazione al posto della divisione.
G5: …………………………………………………………………………………………………………… ………………………………………………………………………………………………………………….
Alla fine del percorso è stato somministrato alla classe un test di verifica tradizionale, del quale pubblico una delle versioni
I risultati sono stati piuù che soddisfacenti:
certamente una valutazione importante sarà da effettuare fra qualche mese per valutare l’effettiva assimilazione degli apprendimenti.
Che cosa ti sembra di aver imparato bene in questo progetto?
Con questo progetto ho imparato a maneggiare molto bene le frazioni e non penso di dimenticarle più. So inoltre che quando mi serviranno le saprò usare senza dovermele ricordare.
Ho imparato a collaborare, prima non volevo partecipare, ma adesso ho imparato il lavoro di squadra
Il materiale ti è sembrato facile da usare? Avresti qualche suggerimento per migliorarlo?
Il materiale è facile da usare; le aste con denominatore piccolo (1/10, 1/12) sono troppo piccole e difficili da maneggiare
Il materiale è maneggevole, resistente e leggero, ma difficile da riordinare
Qual è stata la cosa più curiosa o più interessante?
La cosa più interessante è stata la costruzione delle operazioni; in particolare la moltiplicazione e la divisione per via geometrica e quindi la determinazione della regola.
Per me la cosa più interessante e curiosa è stato scoprire quanto erano importanti i compagni nel lavoro di gruppo
Che cosa ti è sembrato più difficile o che si potrebbe migliorare?
La divisione è stata più difficile, soprattutto fra i rotti;
l’addizione era difficile all’inizio, ma poi ce l’ho fatta
Lavorare in questo modo è diverso dalla lezione tradizionale in cui si studia sul libro e poi si fanno gli esercizi: rispetto al tipo di lavoro tradizionale elenca, secondo te:
I lati positivi:
· Lavorare insieme ed essere più coinvolti ci fa imparare meglio e ci aiuta a risolvere dubbi
· è più divertente e si capisce meglio
· Sono riuscito a capire bene le cose in classe senza fare fatica a casa
· Capisco meglio e mi piace di più
· Impari più facilmente
· Non ci si annoia
· è più rilassante perché è bello lavorare in gruppo
· Studiare e divertirsi allo stesso tempo
I lati negativi:
· Non tutti lavorano nello stesso modo, con lo stesso impegno, specialmente a casa. La collaborazione non è la stessa da parte di tutti, alcuni ne approfittano per non fare niente. La collaborazione è difficile
· Si può pensare che quell’ora sia ricreazione, invece è un’ora di studio
· È difficile trovare le definizioni da soli
· La parte al computer (= scrittura del diario di bordo) è noiosa o difficile per problemi di connessione
· Siamo andati lenti ed è stato un lavoro lungo
Un ringraziamento speciale va al professor Franco Ghione che ci ha permesso di partecipare a questa entusiasmante avventura e alle professoresse Silvia Cerasaro e Laura Tomassi che ,insieme alle loro classi, e con un’assidua collaborazione, ci hanno accompagnato nel nostro percorso.
Roma, 20 dicembre 2019
La classe 2H dell’IC Piazza Winckelmann e la professoressa Marina Furlani
Atzei Giulia |
Battisti Chiara |
Bianchi Giovanni |
Cabiddu Matteo |
Calandrella Lucia Maria |
Carimando Angelica |
Colonna Ludovico |
Comande' Guido |
De Nardo Matilde |
Di Ielsi Angelica |
Ferroni Ludovica |
Folliero Emma |
Galassi Matteo |
Maliglig Matteo Ivan Magtibay |
Nannelli Daniele |
Ruggeri Arianna |
Saccone Giorgia |
Saccone Simone |
Sisti Giulio |
Tripodi Ginevra |
Valeri Edoardo |
Wlaz Gabriel |
