Menù schede didattiche
|
La matematica araba prima di Fibonacci Franco Ghione |

Menù principale
| |
|
Risale al IX secolo la nascita dell’Algebra cioè di una teoria astratta deputata a introdurre e studiare le equazioni e le loro radici. Sappiamo che questo enorme progresso scientifico avvenne a Baghdad nella Casa della Saggezza, una particolare struttura finanziata dallo stato per raccogliere, sotto uno stesso tetto i più importanti filosofi, scienziati, linguisti e giuristi dell’immenso impero arabo. Sappiamo che si deve al matematico al-Khwārizmi (IX sec.) la stesura del primo libro Kitab al-Jabr wa al-muqābala che darà oltre al nome, il via alla nuova disciplina. |
 L’antica Baghdad: la città circolare
| ||||||||
 al-Khwārizmi
|
L’ambiente fortemente interdisciplinare della Casa della Saggezza avrà una influenza non secondaria sull’atto di nascita di questa disciplina immediatamente rivolta alla geometria, all’aritmetica, ma anche al calcolo delle obbligazioni e alla risoluzione dei testamenti sulla base dei vincoli coranici. Anzi sarà proprio questa problematica di carattere squisitamente giuridico a riempire più di due terzi dell’intero trattato. | ||||||||
|
Tra i matematici arabi fu invece colta immediatamente la potenza dei nuovi metodi algebrici e si iniziò da subito ad applicarli ai grandi problemi insoluti della matematica greca come la trisezione dell’angolo o la duplicazione del cubo e, in ambito aritmetico, ai difficili problemi diofantei da poco riscoperti dai traduttori arabi. Abu Kamil (IX secolo), immediatamente successivo ad al- Khwārizmi, iniziò un’opera di revisione, messa a punto e generalizzazione dell’algebra fornendo nuove tipologie di equazioni, e precisando le dimostrazioni con l’uso della geometria euclidea, la sola teoria fondata rigorosamente su dei postulati universalmente riconosciuti che potesse dare alla nuova scienza valore inconfutabile. L’opera di Abu Kamil, non sappiamo se fu mai tradotta in latino, ma comunque era certamente nota a Fibonacci che la riproduce abbondantemente nell’ultimo capitolo del suo Liber abaci lasciando in sospeso possibili ulteriori sviluppi: Fibonacci dopo aver esposto 96 problemi puramente algebrici chiude la sua gigantesca opera con un semplice punto. Punto che avrebbe potuto essere posto alla fine del 95-esimo problema o anche prima. Senza ulteriori commenti senza una conclusione come se volesse con quel punto finale lasciare in sospeso il pensiero dello studioso, lasciare aperto il discorso ad ulteriori fantastici e misteriosi sviluppi. |
| ||||||||
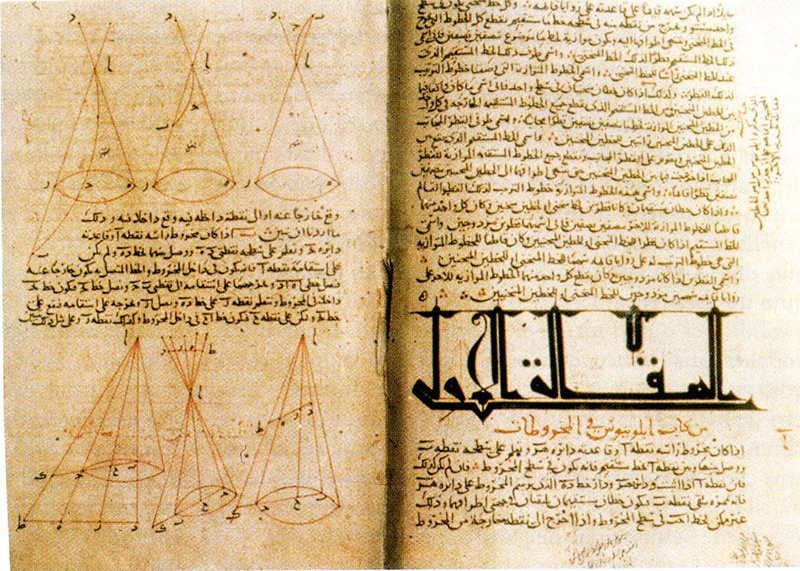 apri la nota Coniche nel mondo arabo |
Queste opere riviste con i nuovi metodi dell’Algebra aprivano immensi campi di ricerca che penetrarono in occidente molto più tardi durante il nostro rinascimento scientifico nel XVI secolo attraverso il lavoro di traduzioni dal greco soprattutto di Maurolico, Commandino e della sua scuola. Le coniche e le superfici quadriche ottenute per rotazione di una conica, fecero ingresso invece molto presto sulla scena della matematica araba. Già Ibn Sahl (X sec) le aveva prese in considerazione e utilizzate per studiare gli specchi e le lenti sulla base di una precisa legge sulla rifrazione della luce, quando passa da un mezzo ad un altro, che troviamo espressa correttamente per la prima volta nella sua opera. | ||||||||
|
|
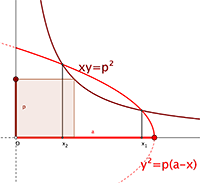
Ma più di ogni altro fu il matematico e poeta al-Khayyam (XI sec) che dopo aver elencato tutti i possibili tipi di equazioni di terzo grado a coefficienti positivi, utilizzò metodicamente le coniche per esprimere le radici dell’equazione attraverso la posizione dei punti di intersezione di due opportune coniche. Ad esempio, per risolvere l’equazione x3+c=ax2 al-Khayyam interseca una iperbole con una parabola. |
||||||||
|
Che le coniche si prestassero magnificamente a una trattazione algebrica dipende dal fatto che esse si portano con loro, in modo intrinseco, una sorta di riferimento cartesiano attraverso il quale è possibile esprimere la posizione di un punto nel piano misurando la sua distanza da due assi di riferimento. |
|||||||||
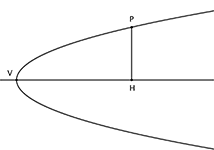 | y2=px | ||||||||
|
Una iperbole è definita dai suoi due asintoti e i punti P dell’iperbole sono caratterizzati, indicando con H e K le proiezioni ortogonali di P sui due asintoti, dalla proprietà che il rettangolo di lati PH e PK ha area costante indipendentemente dalla posizione di P sull’perbole cioè xy=c. |
|||||||||
 | xy=c | ||||||||
 Federico II |
L’opera di Apollonio, di difficile lettura a causa della complessa articolazione di rapporti con rapporti composti di varia natura, riletta in termini algebrici, risultava di più semplice comprensione. La mancanza di queste conoscenze fermò per secoli la matematica occidentale dove si era fermato Abu Kamil ed anche gli sviluppi in ambito aritmetico-diofanteo che presupponevano una teoria completa dei polinomi e delle operazioni tra polinomi compresa la divisione con resto, pienamente sviluppata da al-Karaji (fine del X sec.) e dalla sua scuola, restavano di difficile comprensione ed anche, probabilmente, di scarso interessa in una matematica latina che sempre più tendeva a privilegiare gli aspetti applicativi. La stessa opera di Fibonacci volente o nolente spingeva in questa direzione anche se lo stesso Fibonacci si cimentò in problemi diofantei nel suo Liber quadratorum, dove fornì, per rispondere a un quesito che Giovanni da Palermo gli pose durante la visita di Federico II a Pisa nel 1225, un numero quadrato che resta quadrato anche quando gli si aggiunge o gli si toglie 5: tale numero è (41/12)2 = 1681/144. | 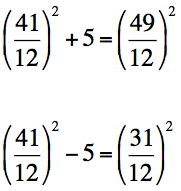 | |||||||
|
Il ’’fiore dell’Algebra’’ non troverà gran seguito nella matematica cristiana successiva a Fibonacci: il punto di sospensione con il quale si chiude il suo Liber abaci resterà tale anche nei successivi trattati in uso nelle scuole d’abaco in latino o in lingua volgare dove i problemi di carattere applicativo giocheranno il ruolo principale. Ma un seme era stato lanciato e, tre secoli dopo, nella prima metà del ’500, alcuni matematici italiani formati in quella scuola riuscirono la dove neppure i matematici arabi erano riusciti, riuscirono a trovare la soluzione per radicali di una equazione generica di terzo grado. | |||||||||