Questo libro, scritto da al-Khwārizmi tra il l’813 e l’833, rappresenta l’atto di nascita dell’Algebra. La parola al-Jabr che da il nome alla disciplina, fu riprodotta nei testi occidentali in varie forme (geber, arcibra, alcibra, argebra, arzibra infine algebra) e significa nella lingua araba restaurare, aggiustare, riparare questo perchè i termini preceduti dal segno meno venivano chiamati naquis cioè termini tolti, amputati e l’equazione doveva essere aggiustata attraverso l’operazione al-Jabr che consiste nell’aggiungere nei due membri dell’equazione il termine tolto. Così, ad esempio

Il temine al-muqābala che significa porre accanto, confrontare indica l’operazione attraverso la quale termini simili in membri diversi di una equazione vengono messi vicini sottraendo il maggiore dal minore. Così, ad esempio, l’equazione

È facile, studiando a priori tutti i casi possibili, trovare tutte le possibili equazioni di primo e secondo grado a coefficienti positivi (i soli che potevano rappresentare una grandezza): si tratta di soli 6 casi che vengono divisi in due classi (binomie e trinomie)

Per ogni caso al-Khwārizmi fornisce un algoritmo per trovare la soluzione che consiste essenzialmente nella descrizione a parole della formula risolutiva.
La correttezza della formula veniva poi dimostrata interpretando i numeri come grandezze geometriche (linee o superfici) e costruendo opportune figure per tradurre l’equazione in forma geometrica.

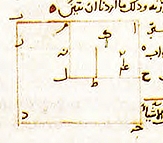
Ad esempio il caso bx+c=ax² (radici più numero sono uguali a quadrati) è descritto nella pagina manoscritta precedente con la figura in basso a sinistra che risolve il problema.
L’algoritmo consiste nel ridurre, come prima cosa, l’equazione a un solo quadrato dividendo ogni coefficiente per il numero a; fatto questo l’equazione si riduce alla tipologia bx+c=x² la cui soluzione, che al-Khwārizmi descrive a parole, è data dalla formula:

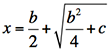Da un punto di vista geometrico, si deve trovare un grande quadrato di lato x che sia costituito da un rettangolo di lati b e x e una ulteriore area residua di grandezza c. Essendo il rettangolo contenuto nel quadrato sarà b < x e la figura quella è in margine.

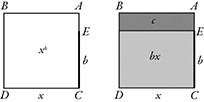
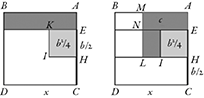
Dividendo EC in due parti uguali col punto H, si dimostra che il quadrato su EH con l’aggiunta del rettangolo di area c (trasformato in uno gnomone) è un quadrato di area nota e lato MA.
La radice di quest’area è quindi nota e x= AC= HC+HA.
Un procedimento analogo è usato in tutti gli altri casi.

Il libro di al-Khwārizmi propone numerosi esempi e problemi per addestrare lo studente a ridurre le equazioni alla forma canonica con le operazioni di al-Jabr e al-muqābala e, una volte ridotte, trovare con la formula opportuna la soluzione positiva (se esiste) del problema.
Nel caso che l’equazione ammetta due soluzioni positive, al-Khwārizmi se la cava consigliando al lettore di scegliere quella che pare più opportuna rispetto al problema che si era posto.

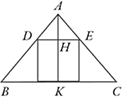
Il testo contiene anche una parte di geometria nella quale si mostra come risolvere un problema geometrico con quello che in Italia sarà chiamato il metodo della cosa. Ecco un esempio: inscrivere in un triangolo isoscele di lati 10, 10 e 12 parti un quadrato come nella figura a margine.Al-Khwārizmi chiama il lato incognito DE del quadrato una cosa e calcola l’area del triangolo sommando le aree dei tre triangolini con quella del quadrato. Questa area così calcolata contiene la cosa e anche la cosa al quadrato. Fatto questo al-Khwārizmi calcola l’area del triangolo direttamente e trova 48. Uguagliando le due aree trova una equazione che può risolvere con i suoi algoritmi: il risultato fornisce il valore della cosa : 4/5.

Una breve parte del trattato con pochissimi esempi è dedicata ai problemi relativi ai cambi, alle transizioni e ai baratti, mentre la parte decisamente più estesa è dedicata ai testamenti. Facciamo un esempio:

Un uomo muore e lascia due figli; ha legato un terzo del suo bene a uno straniero e ha un bene di 10 dirham al quale va aggiunta una somma di 10 dirham che gli deve uno dei suoi due figli (che non possiede nulla).

Il problema è reso complicato dal fatto che il bene da dividere tra i tre eredi comprende 10 dirham e quella parte del debito che il figlio potrà restituire dopo aver incassato la sua eredità. Ma per sapere a quanto ammonta questa somma si deve dividere l’eredità e per dividere l’eredità si deve sapere quanto il figlio potrà restituire. Sembra un circolo vizioso! Ecco come procede al-Khwārizmi.

Chiamiamo una cosa la parte di debito che il figlio riesce a restituire usando la sua parte di eredità; 10 più una cosa è dunque il bene da dividere:1/3 allo straniero e il resto in parti uguali ai due figli, quindi 1/3 ciascuno.
Il figlio indebitato prenderà un terzo di 10 più una cosa ma questo è uguale a una cosa perchè una cosa è, come abbiamo detto, la parte di eredità spettante al figlio indebitato.

Così con i nostri simboli, chiamando una cosa con x, troviamo l’equazione:

Il libro di al-Khwārizmi è stato tradotto in Italiano a partire dalla traduzione francese del testo originale e si trova in: