pagina iniziale capitolo dodicesimo del Liber abaci - seconda parte<br>Conv. Sopp. C.I. 2616, BNCF, folio 71 recto
seconda parte cap XII
 
Seconda parte

Inizia la parte seconda sulla proporzione dei numeri.
pg.170

 (XII.2.1 ; G: XII.26) U
n numero ha con un altro numero una proporzione uguale o maggiore o minore. Uguale quando i numeri sono uguali tra loro, come 3 e 3. I numeri che sono tra loro in proporzione maggiore, hanno la proporzione secondo ciò che viene dalla divisione del numero maggiore per il minore, come 8 a 4, che sono in doppia proporzione, poiché 8 diviso per 4, fa 2; o perché 8 è il doppio di 4. Ugualmente 9 a 3 sono in tripla proporzione; perché il 9 è il triplo di 3. E 16 a 5 sono in tripla proporzione più un quinto; perché 16 diviso 5 fa
1
5
3. E così s'intenda per gli altri che sono in proporzione maggiore. I numeri che sono in proporzione minore sono in quella proporzione che viene dalla divisione del numero minore per il maggiore, come 4 a 8, che sono in proporzione dimezzata perché 4 diviso per 8 fa la metà di uno; o perché 4 è la metà di 8. Ugualmente 3 a 9 sono in proporzione di un terzo; poiché 3 è un terzo di 9, e 5 a 16 sono in proporzione di
5
16 di uno intero perché 5 diviso 16 fa proprio
5
16 di uno intero.
(XII.2.2 ; G: XII.28) S
e si volesse saper a quale numero il 6 sta nella stessa proporzione del 3 rispetto al 5, farai così. Moltiplica 5 per 6, farà 30 ; dividilo per 3, farà 10 che è il numero che cerchi; poiché come il 3 sta al 5 così il 6 sta al 10. Si è soliti, invece, per nostro uso comune, proporre questo stesso problema in un altro modo: cioè se il 3 fosse 5 cosa allora sarebbe il 6: quando il problema è posto in questo modo, si moltiplica similmente il 5 per il 6, e si divide il totale per 3. Ugualmente si chiede a quale numero l'11 stia nella stessa proporzione del 5 rispetto al 9: cioè, secondo l'uso comune, se il 5 fosse 9, quale numero sarebbe 11. Moltiplicherai dunque il 9 per l'11 e dividerai per 5, farà
4
5
19 che è il numero trovato in base alla domanda. 		Se a fosse b cosa sarebbe c?
a : b = c : ?
? = c × 
b
a

  

Un altro metodo per le proporzioni.

(XII.2.3 ; G: XII.30) S
e venisse detto che 7 fosse la metà di 12 quanto sarebbe la metà di 10: ebbene questa situazione può essere intesa in due modi, cioè quando si dice: se 7 fosse la metà di 12; o si intende che la metà di 12, che è 6, cresce nel 7, o che il 7 diminuisce nella metà di 12, cioè in 6. Donde se il 6, che è la metà di 12, cresce nel 7, quindi cresce anche la metà di 10: e allora avrai bisogno di tale regola: moltiplicherai 7 per 10, e dividerai per 12, farà
5
6
5 per [ l’aumento ] della la metà di 10; e se vogliamo intendere che il 7 diminuisca nel 6, cioè nella metà di 12, dunque anche la metà di 10 diminuisce; e allora moltiplicherai il 6 scritto sopra per la metà di 10, cioè per 5, farà 30; dividilo per 7, farà
2
7
4; e tanto starebbe allora alla metà di 10. E così potrai risolvere simili problemi con il metodo che vorrai tra i due metodi descritti precedentemente. Tuttavia noi usiamo rispondere sempre con il primo metodo a chi ci interroga.
122 : 7 =
102 : ?

7 :
122  =
102 : ?

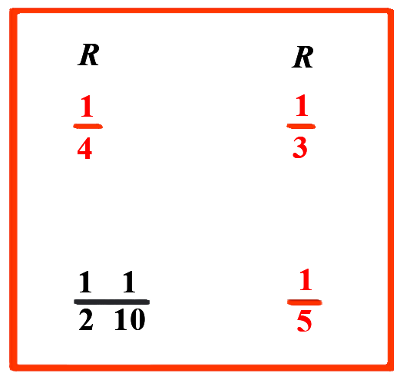
(XII.2.4 ; G: XII.32) S
e
1
3 fosse
1
4, quanto sarebbe
1
5: questa domanda è come se si dicesse:
1
3 di un rotolo si vende per
1
4 di un bisante; quanto vale
1
5 di un rotolo? Perciò bisogna scrivere questa domanda alla maniera delle transazioni commerciali, e fare i calcoli secondo ciò che abbiamo insegnato per casi simili nell'ottavo capitolo.
pg.171
(XII.2.5 ; G: XII.33) S
e si chiedesse di trovare quattro numeri interi proporzionali, il primo dei quali stia al secondo come il terzo al quarto; cioè che la parte, o parti che il primo numero sarà del secondo, la stessa parte o parti il terzo numero sarà del quarto: o come il primo sia multiplo del secondo, così sia il terzo lo stesso multiplo del quarto numero: poni per il primo e il secondo numero due numeri a piacere, come vuoi. E il primo numero sia 3 e il secondo 7; e come terzo numero poni un numero che possa essere diviso interamente per il primo numero. E sia 6; e dividi il 6 per il primo numero, cioè per 3, farà 2; per questo 2 moltiplica il secondo [NdT]
Secondo il senso, ipsum
  ci sembra un chiaro errore
numero, cioè 7, farà 14 che è il quarto numero. Di conseguenza, 3 è dunque i tre settimi di 7. Similmente anche 6 è
3
7 di 14. Puoi anche avere 14 come primo numero; 6 per secondo; 7 per terzo; 3 per quarto: perciò quanto il 14 è multiplo di 6 tanto il 7 è multiplo di 3: il 14 infatti è soltanto due volte, e un terzo di 6, e altrettanto il 7 è multiplo di 3: e si noti che quando quattro numeri saranno proporzionali nel modo detto prima, dunque il primo starà al terzo come il secondo al quarto: infatti il primo 3 sta al terzo 6 come il secondo 7 sta al quarto 14: infatti ogni numero antecedente è la metà del suo conseguente: e si consideri ancora, che tra quattro numeri proporzionali il prodotto della moltiplicazione del primo numero per
(PdA)
Anche la costruzione con in + acc. non manca tuttavia di qualche sporadico esempio nel Liber abbaci. L’espressione è chiaramente influenzata dal volgare, giacché de + abl. si sostituisce al genitivo.  [PdA,pag.10]
il quarto sia sempre uguale al prodotto della del secondo per il terzo. Come qui, dove la moltiplicazione di 3 per 14 fa quanto la moltiplicazione di 6 per 7.
3 : 7 = 6 : 14

(XII.2.6 ; G: XII.36) U
gualmente così come il primo numero sta al secondo e il terzo al quarto così il quinto sta al sesto. Trovati in primo luogo quattro numeri proporzionali, come sopra, poni un quinto numero a piacere, che si divida interamente per il primo numero. Sia 15, che diviso per 3, fa 5; per il quale moltiplica il secondo numero 7, farà 35, che è il sesto numero.

(XII.2.7 ; G: XII.37) E se sia proposto di dividere il 10 in quattro parti diverse proporzionali tra loro cioè che la prima moltiplicata per la quarta, faccia quanto la moltiplicazione della seconda per la terza; prima troverai i quattro numeri proporzionali, e siano 3, e 7, e 6 ,e 14, e sommali insieme, farà 30; di cui 10 è la terza parte. Perciò prendi la terza parte dei quattro numeri posti; e avrai come prima parte 1; come seconda parte
1
3
2; come terza 2; come quarta
2
3
4: e sappi che
(PdA)
In dipendenza da verba dicendi e sentiendi, accanto alle infinitive oggettive, sono abituali nel Liber abbaci le dichiarative introdotte da quod o quia (assai diffuse già nel sec. IV d.C. anche nella lingua letteraria), talora costruite con il congiuntivo.  [PdA,pag.10]
tale proporzione si chiama proporzionalità. Ebbene c’è una certa proporzione che si chiama continua, nella quale tutti i numeri sono in ordine tra loro in una stessa proporzione; cioè come il primo numero sta al secondo, così il secondo sta al terzo, e il terzo al quarto, e il quarto al quinto; e così via in successione ogni numero sta ad ogni altro numero.
a
1 : a
2 =  a
2 : a
3 = 
a
3 : a
4 =  a
4 : a
5 =  ...




(XII.2.8 ; G: XII.39) S
e vorrai trovare numeri che stanno in proporzione continua, per quanti siano, poni come primo numero quello che vuoi, come secondo un qualche multiplo del primo, come il doppio, o il triplo, o un qualsiasi altro multiplo; e poni come terzo un multiplo del secondo tanto quanto il secondo lo è rispetto al primo. Allo stesso modo come il terzo sia multiplo del secondo, poni un quarto che sia lo stesso multiplo del terzo, e il quinto del quarto, e ciascuno del proprio antecedente. Per esempio: vogliamo trovare cinque numeri in proporzione continua. Sia allora 1 il primo di questi; il secondo 2, cioè il doppio del primo; il terzo il doppio del secondo, cioè 4; il quarto il doppio del terzo, cioè 8; il quinto il doppio del quarto, cioè 16: 1 è dunque la metà di 2; come 2 lo è di 4, e 4 di 8, e 8 di 16. Similmente come 16 è il doppio di 8, così 8 è il doppio di 4; e 4 di 2; e 2 di 1: e così puoi porre ciascun [ conseguente ] triplo dei numeri, o trovare un qualsiasi altro multiplo del suo antecedente.
pg.172
(XII.2.9 ; G: XII.41) E si noti, che qualora tre numeri siano in proporzione continua, la moltiplicazione del primo per il terzo farà quanto la moltiplicazione del secondo per se stesso. Per esempio: siano in proporzione continua 3, e 9, e 27: infatti la moltiplicazione di 3 per 27 è uguale alla moltiplicazione di 9 per se stesso, cioè 81: e quando quattro numeri sono in proporzione continua, la moltiplicazione del primo per il quarto è uguale alla moltiplicazione del secondo per il terzo; e la moltiplicazione del primo per il terzo è uguale alla moltiplicazione del secondo per se stesso; e la moltiplicazione del secondo per il quarto, è uguale alla moltiplicazione del terzo per se stesso. Così se il primo numero fosse 1; il secondo 2; il terzo 4; il quarto 8, potrai imparare grazie a questi numeri ciò che abbiamo detto. Similmente, quando più numeri sono in proporzione continua, la moltiplicazione degli estremi è sempre uguale alla moltiplicazione degli altri estremi restanti; e ciò finché non sarà rimasto un numero in mezzo agli altri numeri della proporzione. Per esempio: se nove numeri fossero proporzionali, la moltiplicazione del primo numero per il nono sarà quanto la moltiplicazione del secondo per l'ottavo; e del terzo per il settimo; e del quarto per il sesto; e del quinto, che è nel mezzo della proporzione, per se stesso. Per chiarire ciò, siano nove numeri in proporzione continua: 1, e 2, e 4, e 8, e 16, e 32, e 64, e 128 e 256: infatti la moltiplicazione di 1 per 256 è uguale alla moltiplicazione di 2 per 128, e di 4 per 64, e di 8 per 32, e di 16 per se stesso. Su questo infatti si fonda la tecnica del moltiplicare le figure, che abbiamo insegnato nel secondo capitolo, come è scritto nel medesimo capitolo.


a
1 : a
2 =  a
2 : a
3 =  a
3 : a
4


a
1 × a
4 =  a
2 × a
3
a
1 × a
3 =  a
2 × a
2
a
2 × a
4 =  a
3 × a
3

(XII.2.10  ; G: XII.44) S
e si chiedesse di trovare due numeri, dei quali i
2
7 di uno siano
3
8 dell'altro, moltiplicherai in croce 7 per 3, e 8 per 2, e avrai come primo numero 21; e come secondo 16: infatti il 6 è
2
7 di 21 e
3
8 di 16: ebbene questa regola si fonda su quelle che seguono; poiché
2
7 di
3
8 di un qualunque numero sono uguali ai
3
8 di
2
7 del medesimo numero. Perciò quando moltiplichiamo 7 per 3, otteniamo
3
8 di 56; questo 56 viene fuori dalla moltiplicazione di quel 7 per quell’ 8 che sono sotto le linee di frazione, poiché la proporzione di 3 a 8, è la stessa proporzione che c'è fra 3 settimi e 8 settimi; e quando moltiplichiamo 8 per 2, otteniamo i
2
7 di questo 56. Per cui
2
7 di 21, cioè di
3
8 di 56, sono quanto
3
8 di 16, cioè
2
7 di 56.
Cerca soluzioni intere di

2
7 x =
3
8 y

2
7 ⎧⎩
3
8 A⎫⎭ =
3
8 ⎧⎩
2
7 A⎫⎭

A = 56

(XII.2.11 ; G: XII.45) A
ncora
1
4
1
3 di un numero siano uguali a
1
5
1
4 dell'altro, riporta
1
4
1
3 nelle parti di un solo numero, sarà
7
12; farai lo stesso di
1
5
1
4, farà
9
20. Quindi
7
12 del primo numero sono uguali ai
9
20 del secondo. Perciò, secondo l’ordine definito sopra, moltiplicherai 12 per 9 e 20 per 7, e avrai come primo numero 108; come secondo 140: che possiamo anche semplificare in numeri minori, poiché ciascuno di questi stessi numeri può essere diviso interamente per 4. Perciò se considerassimo la quarta parte di ciascuno, avremo allo stesso modo come primo numero 27; e come secondo 35: o altrimenti poiché in ciascuna delle due moltiplicazioni scritte sopra si moltiplica il numero la cui quarta parte è intera, la prima delle quali è 12, la seconda 20. Allora moltiplica solo la quarta parte di 12 per 9, e la quarta parte di 20 per 7, e avrai similmente 27 e 35.

(XII.2.12 ; G: XII.47) D
i nuovo
1
5
1
4
1
3 del primo numero siano uguali a
1
6
1
5
1
4 del secondo; riporta similmente
1
5
1
4
1
3 nelle parti di un solo numero, farà
47
60. Fa lo stesso per
1
6
1
5
1
4, farà
37
60; e moltiplicherai il 60, che sta sotto il 47 per il 37; e il 60 che sta sotto il 37 per il 47: o, per avere numeri più piccoli, moltiplicherai soltanto i sessantesimi di 60 per il numero che gli si oppone in diagonale e avrai come primo numero 37; come secondo 47: e così puoi procedere in casi simili.



proporzioni.py
(XII.2.13 ; G: XII.48) U
gualmente ci sono tre numeri, dei quali i
2
5 del primo sono uguali ai
3
7 del secondo e ai
4
9 del terzo: poni le parti scritte prima in ordine così:
4
9
3
7
2
5. E moltiplicherai ciascun numero che si trova sotto la linea di frazione per il numero che sta sopra una delle due linee di frazione rimaste, e moltiplicherai il totale per l'altro numero, che è sopra l'altra linea di frazione, e avrai i numeri che cerchi. Per esempio: moltiplicato il 5, che sta sotto la prima linea di frazione, per il 3, che sta sopra il 7; e il risultato per il 4 che sta sopra il 9, avremo come primo numero 60. Ugualmente moltiplicherai il 7 per il 4; e il risultato per il 2, farà come secondo numero 56. E ancora, moltiplicato il 9, che sta sotto la terza linea di frazione, per 3, e per 2, otteniamo come terzo numero 54.


Cerca soluzioni intere di

2
5 x =
3
7 y =
4
9 z
pg.173
 (XII.2.14 ; G: XII.50) E se vuoi sapere su cosa si fondi questa regola, considera che
2
5 di
3
7 di
4
9 di un qualunque numero sono quanto i
3
7 dei
4
9 dei
2
5 dello stesso numero; e quanto i
4
9 dei
3
7 dei
2
5 del medesimo numero: considerati questi elementi capirai che noi più sopra abbiamo preso i
4
9 di
3
7 del numero che è risultato dalla moltiplicazione di 9 per 7 per 5, cioè di 315: come quando abbiamo moltiplicato 5 per 3 e per 4, da cui abbiamo ottenuto 60. Similmente quando ottenemmo 56, calcolammo
4
9 di
2
5 di 315: e ancora quando ottenemmo il 54, prendemmo i
3
7 dei
2
5 di 315. Di cui
2
5 di 60, che sono
3
7 di
4
9 di 315, sono quanto i
3
7 di 56, che sono
4
9 di
2
5 di 315; e quanto
4
9 di 54, che sono i
3
7 di
2
5 dello stesso 315. Infatti il 24 è uno dei suddetti prodotti che provengono dalla moltiplicazione di 2 per 3 per 4: si possono anche avere numeri più piccoli se trovati i tre numeri, cioè 60, e 56, e 54, li avrai divisi per 2 che è la loro regola comune [NdT]
Il massimo comun divisore
: e il primo numero sarà 30, il secondo 28, il terzo 27.
  
2
5 ×
3
7 ×
4
9 × 5 × 7 × 9 		=
=
3
7 ×
2
5 ×
4
9 × 5 × 7 × 9 		=
=
4
9 ×
2
5 ×
3
7 × 5 × 7 × 9 		 
(XII.2.15 ; G: XII.52) E se si proponesse che
1
4
1
3, cioè
7
12 del primo numero sia
1
5
1
4, cioè
9
20 del secondo, e
1
6
1
5, cioè
11
30 del terzo, scrivi in ordine
11
30
9
20
7
12, e moltiplicherai 12 per 9; e per 11; e 20 per 11; e per 7; e 30 per 9; e per 7; e semplificherai
1
2 da ciascuna moltiplicazione, e avrai come primo numero 594, come secondo 770, come terzo 945.

(XII.2.16 ; G: XII.53) U
gualmente ci sono tre numeri, dei quali
1
3 del primo è quanto
1
4 del secondo; e
1
5 del secondo è quanto
1
6 del terzo numero: trova prima i due numeri, dei quali
1
3 di uno è
1
4 dell’altro: saranno 3, e 4: dopo ciò troverai altri due numeri, dei quali
1
5 di uno sia
1
6 dell'altro, e saranno 5 e 6; quindi il primo numero sta al secondo, come 3 sta a 4 [NdT]
3  è un chiaro errore
; e il secondo al terzo come il 5 sta al 6: perciò poni 3 e il 4 su una stessa riga; e il 5, e il 6 su un'altra; così che
(PdA)
Nei capitoli XII-XV del Liber abbaci si contano altri tredici esempi di ita quod consecutivo, sei volte con il congiuntivo.  [PdA,pag.11]
il 5 sia sopra il 4, come qui si mostra: e moltiplicherai 5 per 3, e 5 per 4, e 4 per 6, e avrai come primo numero 15; come secondo 20; come terzo 24. Per esempio: 3 sta a 4, così un qualche multiplo di 3 sta allo stesso multiplo di 4: dunque come 3 sta a 4, come il quintuplo di 3, cioè 15, sta al quintuplo di 4, cioè a 20. Ugualmente come 5 sta a 6, così un certo multiplo di 5 sta allo stesso multiplo di 6: dunque come il 5 sta al 6, così il quadruplo di 5, cioè 20, sta al quadruplo di 6, cioè a 24: il primo numero trovato, il 15, sta al secondo, il 20, come 3 sta a 4; e il secondo, 20, sta al terzo, 24, come 5 sta a 6 come esigevamo che fosse.

1
3 x =
1
4 y
1
5 y =
1
6 z

proporzioni multiple
multi_proporzioni.py
(XII.2.17 ; G: XII.56) E se si proponesse, che i numeri siano quattro; e di essi sia il primo, sia il secondo, sia il terzo siano tra loro nelle proporzioni scritte sopra; e che i 2/5 del terzo numero siano i 3/7 del quarto numero; troverai prima i tre numeri scritti sopra, cioè 15, e 20, e 24: poi troverai due numeri, dei quali i 2/5 di uno siano uguali ai 3/7 del quarto numero, saranno 15 e 14: e li scriverai sopra gli altri tre numeri, come qui si mostra; e moltiplicherai 15, che è sopra il 24, per 15, e poi per 20 e infine per 24; e moltiplicherai il 14 per 24, e avrai il primo numero 225; e il secondo 300; e il terzo 360, e il quarto 336: e il terzo numero sta al quarto come 15 sta a 14; essendo i 2/5 del terzo numero uguali ai 3/7 del quarto: e così puoi trovare molteplici numeri in qualunque proporzione.

1
3 x =
1
4 y
1
5 y =
1
6 z
2
5 z =
3
7 w

Termina la seconda parte del dodicesimo capitolo.