
Inizia il capitolo dodicesimo
|
||
|
(XII.1.1 ; G: XII.1)
Dividiamo dunque in nove parti il capitolo dodicesimo sui problemi dell’abbaco. La prima di queste è sulle somme dei numeri e di alcuni problemi simili. La seconda sulle proporzioni dei numeri con la regola del quarto proporzionale. La terza sui problemi di alberi, e di altre cose simili, per i quali ci sono le soluzioni. La quarta sul ritrovamento delle borse. La quinta sull'acquisto di cavalli tra consoci, secondo una data proporzione. La sesta sui viaggiatori e sui problemi che sono simili ai problemi dei viaggiatori. La settima sulle restanti questioni erratiche che si diversificano nelle loro regole. La ottava su alcune divinazioni. La nona sulla duplicazione della scacchiera e su altre questioni. |
||
Si espongono le parti del XII capitolo.
Inizia la parte prima sulla collezione dei numeri. |
||
| pg.167 | (XII.1.2 ; G: XII.3) Quando poi insieme a un numero dato vuoi raccogliere [ sommare ] altri numeri a piacere, che salgono dal numero dato in modo uguale, o aumentando di un’unità, o di 2 o di 3 o di qualsiasi altro numero, moltiplica la metà della quantità dei numeri raccolti per [ la somma di ] quelli all’estremo; oppure moltiplica la metà della somma degli estremi, cioè del primo e dell'ultimo numero, per la quantità dei numeri raccolti, e avrai quanto cercato. Per esempio: voglio raccogliere sopra il 7 i numeri che salgono da questo sette di tre in tre fino al 31, come 7, e 10, e 13, e così via fino a 31. La quantità dei numeri predetti è 9, cioè ci sono nove numeri nella predetta raccolta; tra questi uno è il sette, e gli altri che restano sono otto, che equivale alla terza parte di 24, che è il resto di 31 meno 7. L'addizione poi degli estremi, cioè di 7 e di 31, è 38. Perciò se moltiplicherai la metà di 9 per 38, o la metà di 38 per 9, avrai 171 come somma della raccolta dei nove numeri posti: con questa regola si possono trovare le raccolte scritte sotto, che mostreremo anche in un altro modo. | Progressioni aritmetiche 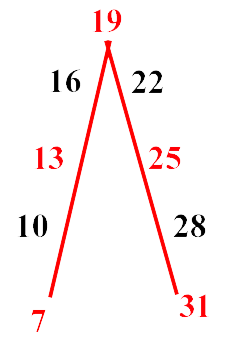
|
Dello stesso in altro modo
|
||
(XII.1.3 ; G: XII.6) Se vuoi raccogliere [ sommare ] alcuni numeri che ordinatamente salgono o per l'aumento di un’unità, cominciando da 1, o per l'aumento di 2, iniziando da 2, o per l'aumento di qualche altro numero cominciando da esso, dividi l'ultimo numero per il primo, e somma uno al risultato della divisione; e serba ciò che ne sarà venuto fuori; e moltiplicalo per la metà dell'ultimo numero, o moltiplica l'ultimo numero per la metà del numero serbato. Per esempio: voglio raccogliere tutti i numeri che sono da 1 fino a 60: dividerò dunque 60 per 1, e addizionerò 1 al quoziente, farà 61, che moltiplicherò per la metà di 60, o moltiplicherò 60 per la metà di 61, 1830 sarà la somma della detta raccolta. Similmente se vuoi raccogliere partendo dal 2 i numeri che salgono di due in due 2 fino a 60, cioè i numeri pari, dividi 60 per 2, e somma l'1, farà 31, che devi moltiplicare per la metà di 60. Similmente se vuoi raccogliere da 3 fino a 60, salendo di tre in tre, come 3, e 6, e 9, moltiplica 1 più la terza parte di 60, cioè 21, per la metà di 60, farà 630; e impara a fare così nei restanti casi simili. |
a + 2a + ... + na = ⎧⎩naa + 1⎫⎭ na2
|
|
|
(XII.1.4 ; G: XII.8)
E allora se vuoi raccogliere solo numeri dispari
[NdT]
abbiamo corretto in partes con impares per coerenza col testo matematico
, cominciando da 1 fino a un qualunque altro numero, puoi procedere in base alla regola precedente. O, il che è lo stesso, moltiplica la metà della somma degli estremi per se stessa, e avrai il risultato cercato. Per esempio: se vuoi raccogliere i numeri dispari, da 1 a 19, moltiplica la metà della somma degli estremi, cioè 10, per se stessa, cioè per il numero che esprime la loro quantità. Infatti i numeri dispari da 1 fino a 19 sono 10; farà 100 per la detta raccolta.
|
1 + 3 + 5 + ... + 2n-1 = n2
|
|
 somma di n numeri quadrati |
(XII.1.5 ; G: XII.12) Se poi vuoi avere la somma dei quadrati di tutti i numeri che vanno in ordine dal quadrato dell’unità, cioè da uno fino al quadrato di un altro numero, diciamo, fino al quadrato di 10, cioè 100; poni il 10, e davanti ad esso poni il numero seguente, cioè 11; e poni sotto di essi la loro somma, cioè 21; moltiplica 10 per 11; e per 21, e dividi il totale per 6, e per 1, che è la differenza tra 10 e 11; avrai 285 per la detta somma; e sarà sempre possibile semplificare per il 6, in questa divisione. E se vuoi avere la somma dei quadrati, dei numeri dispari fino al quadrato del 9, davanti al 9 poni il numero seguente, cioè 11; e poni sotto di essi la loro somma, cioè 20; e moltiplica tra loro questi tre numeri; e dividi il totale per 12, cioè per 6, e per 2, che è la differenza tra 9 e 11, e semplifica, cioè moltiplica la terza parte di 9 per la quarta di 20, farà 15; moltiplicalo per 11, farà 165; e questo è il totale. E se vuoi avere in ordine la raccolta dei quadrati dei numeri [ pari ] a partire dal quadrato di due, che è 4, fino al quadrato di dieci, che è 100, poni il 10 e il pari seguente, cioè 12; e la loro somma, cioè 22. E, nel modo scritto sopra, prendi la dodicesima parte della loro moltiplicazione, che sarà la somma richiesta: ma semplificherai 112 e avrai 220. Similmente puoi avere la somma di tutti i quadrati dei numeri che salgono ordinatamente di 3 in 3, o di 4 in 4, o di qualsiasi altro numero. Così se vuoi ottenere la somma dei quadrati dei numeri ascendenti di 4 in 4, iniziando dal quadrato di quattro, che è 16, fino al quadrato di un altro numero, diciamo fino al quadrato di 20, che è 400; poni prima il 20, e con esso poni il numero seguente che sale di 4, cioè 24: sotto di essi poni il 44, cioè la loro somma; e moltiplica 20 per 24; e per 44, e dividi il risultato per 6, e per il numero che sale di 4, cioè: moltiplica il 20 per un quarto di un sesto di 24, cioè per 1, e per 44, farà 880; e così sarà negli altri casi. Ho dimostrato infatti geometricamente le cose che qui sono dette sulla raccolta dei quadrati nel libro che ho composto sui quadrati. |
1 2 + 2 2 + 3 2 + ... + n2 =
= (2n+1)(n+1)n6
1 2 + 3 2 + 5 2 + 7 2 + 92 =
= (9+11)×11×92×6
2 2 + 4 2 + 6 2 + 8 2 + 102 =
= (10+12)×12×102×6
a 2 + (2a) 2 + (3a) 2 +... (na)2 =
= (2n+1)(n+1)n6a 2
|
Dei due viaggiatori, dei quali uno riproduce l'altro con la crescita ordinata dei numeri
|
||
(XII.1.6 ; G: XII.14) Mostrate dunque le regole della raccolta dei numeri, ora invero si mostrano casi ad esse pertinenti, come è stato annunciato. Ci sono due uomini, che avevano deciso di percorrere un lungo cammino, uno di loro percorreva 20 miglia al giorno, l'altro invece nel primo giorno 1 miglio, nel secondo 2, nel terzo 3; e così aggiungendo sempre un miglio al giorno cercava di perfezionare il suo cammino; si chiede in quanti giorni l'uno raggiungerà l'altro; questo si trova così: duplica il 20, fa 40; da cui sottrai 1, resta 39; in altrettanti giorni l’altro è raggiunto. Infatti chi ogni giorno percorreva 20 miglia, in 39 giorni ha percorso 20 miglia per 39, che furono in totale 780. L'altro negli stessi 39 giorni percorse tante miglia, quante ce ne sono nel totale dei numeri da 1 a 39; la cui somma si trova similmente dalla moltiplicazione di 20 per 39. |
20 n = 1 + 2 + 3 + ... + n =
1+n2n
|
|
Altrimenti di due viaggiatori, uno dei quali segue l'altro salendo per gli stessi numeri.
|
||
(XII.1.7 ; G: XII.16) Ugualmente nel caso che uno percorra ogni giorno 21 miglia; e un altro invece percorra miglia in numeri dispari disposti in ordine, cioè cominciando da uno, fino a raggiungerlo. È chiaro, che lo raggiungerà in 21 giorni, perché se prendiamo ordinatamente 21 numeri dispari, la loro raccolta sarà da 1 fino a 41, e la raccolta dei numeri dispari che sono da 1 a 41, equivale alla moltiplicazione del 21 per se stesso. |
21 n = 1 + 3 + ... + 2n - 1 = n2

|
|
Di due viaggiatori, dei quali l'uno raggiunge l'altro con i numeri pari.
|
||
(XII.1.8 ; G: XII.17) Invece nel caso che uno percorra ogni giorno 30 miglia, l’altro invece faccia il suo cammino aggiungendo numeri pari fino a raggiungerlo, si deve fare così. Togli 1 da 30, resta 29; e in altrettanti giorni lo ha raggiunto. Perché 29 numeri pari ascendono da due fino al 58. E poiché la somma della raccolta dei numeri pari fino a 58 viene dalla moltiplicazione di 29 per 30, non ci sono dubbi che quello lo abbia raggiunto. |
30 n = 2 + 4 + ... + 2n

|
|
Altrimenti nel caso di uno che raggiunge l'altro con l’aumento di tre in tre o di qualche altro numero.
|
||
| pg.169 | (XII.1.9 ; G: XII.18) Ma nel caso che uno percorra ogni giorno un certo numero di miglia, che sia divisibile esattamente per l’aumento quotidiano delle miglia dell'altro, che procede aumentando i numeri di tre in tre, o di quattro in quattro, o di cinque in cinque, o di qualche altro numero, fino a raggiungerlo; bisogna fare così: dividi il numero delle miglia, che il primo percorre ogni giorno, per l'aumento dell'altro, duplica ciò che ne sarà venuto, e da questa somma duplicata togli 1; il resto sarà la quantità di giorni in cui lo raggiungerà. Per esempio: si supponga che uno percorra ogni giorno 60 miglia, e l’altro invece vada salendo di tre in tre, cioè 3 miglia il primo giorno; 6 miglia il secondo; 9 miglia il terzo; dividi 60 per 3, fa 20; duplicalo, fa 40; da cui sottrai 1, resta 39: e in altrettanti giorni quello vien raggiunto; perché i 39 numeri che salgono di 3 in 3 arrivano fino al triplo di 39, cioè fino a 117. La raccolta infatti dei numeri che salgono di tre in 3 fino a 117, equivale alla moltiplicazione di 39 per 60, come si è trovato con la prima regola. E quello che ogni giorno percorreva 60 miglia, percorse similmente in quei 39 giorni 39 per 60 miglia. |
(a b) n = a + 2a + ... + na

|
Dello stesso con un aumento di cinque.
|
||
(XII.1.10 ; G: XII.21) Ugualmente se uno segue l'altro aumentando di cinque in cinque, raddoppiato il quinto di 60 e sottratto da lì uno, troverai 23 come numero della somma dei giorni: e così si può fare per qualsiasi aumento di altri numeri. |

|
|
Altrimenti nel caso il numero di miglia di quello che ogni giorno cammina nello stesso modo non sia divisibile esattamente per l'aumento dell'altro.
|
||
(XII.1.11 ; G: XII.22) Ma se il numero di quello che procede sempre in modo uguale, non può in nessun modo essere diviso esattamente per l'aumento dell'altro, sarà da fare in maniera diversa da quella detta finora: cioè si supponga che quello che va in modo uguale, percorra ogni giorno 10 miglia; e l'altro invece lo segua con un aumento di tre in tre; prendi un terzo di 10 che è 133 e raddoppialo, fa 236; togli 1, resta 235: togli anche le frazioni, cioè 23, resta 5; all’incirca in altrettanti giorni lo ha raggiunto. Ma affinché tu conosca la loro vera somma, vedi quanto fa in 5 giorni quello che cammina in modo uguale. Ebbene, percorre 50 miglia. L'altro invece negli stessi 5 giorni va secondo numeri che aumentano da 3 fino a 15, cioè salendo di tre in tre, percorre solo 45 miglia; da qui fino a 50 ne mancano 5, conservalo. E poiché è chiaro che in questi 5 giorni non lo ha raggiunto, si dovrà considerare il cammino del sesto giorno. In questo sesto giorno quello che sale di tre in tre, percorre 18 miglia, l'altro invece ha continuato a percorrere ugualmente 10 miglia; da queste 10 miglia fino a 18 ne mancano 8; per questo numero dividi il 5 serbato, farà 58 che devi sommare con i 5 giorni più sopra calcolati, farà 585; e in tanti giorni lo ha raggiunto. |
a n = b + 2b + 3b + ... + nb

|
|
(XII.1.12 ; G: XII.25) Altrimenti dividi il totale delle miglia di quello che procede salendo di 3 in 3 nei 5 giorni detti prima, cioè 45, per l'8 ora trovato, farà similmente 585, come abbiamo detto prima: e così si può procedere per tutti i casi simili. |

|
|
Termina la prima parte del dodicesimo capitolo.
|
|
|