
|
Parte Prima
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Prima parte
Inizia l’ottavo capitolo sul procurarsi il prezzo delle merci nel modo migliore |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| pg.84 |
(VIII.1.1; G: VIII.1)
E così in tutti i grandi commerci si trovano sempre quattro numeri proporzionali tre dei quali sono noti mentre l’altro non si conosce: senza dubbio il primo di quei tre numeri noti è il numero della vendita di una qualunque merce, sia che riguardi la quantità, o il peso, o la misura. Un numero come cento pelli, o cento caproni e simili: o anche pesi come il cantaro
(PdA)
, o il centone
[NdT]
1 Centone (centum) = 100 libbre
, o la libbra
[NdT]
1 Libbra (libbre) = 12 once (unce)
, o l’oncia e simili. O di una misura come metrete d’olio
[NdT]
Metrete d’olio (metra olei) =
In Egitto l’unità di peso delle spezie era il fulfulī, una varietà del raṭl (lat. rotulus), la centesima parte del ḳinṭār (da cui lo sp. quintal e l’it. quintale, ma anche il lat. cantare o cantar(i)um o cantarus e l’it. cantàro; cf. gr. κεντηνάριον — kentenàrion).Assai diffuso era anche il djarwī, un tipo di raṭl utilizzato in origine per pesare l’olio. In genere 1 ḳinṭār fulfulī equivale a 144 libre (quasi kg. 4,5), 1 ḳinṭār djarwī a 312 libre (oltre kg. 9,5). [PdA,pag.5]
unità di misura greca per liquidi, corrispondente a circa 38 litri , sestari di frumento [NdT] Sestare di frumento (sexstaria) = ;unità di misura per granaglie , e canne di panni e simili. Il secondo poi è il costo di quella vendita, cioè di quel primo numero, sia che sia una quantità di qualsivoglia denari, o bisanti [NdT] Bisanti (bizantis) = moneta d’oro coniata a Bisanzio , o tareni [NdT] Tareno (tarenus) = Moneta d’oro araba usata anche nell’Italia meridionale , o di qualunque altra delle monete correnti. E il terzo quando ci sarà una qualche quantità della merce in vendita, il cui costo, cioè il quarto numero, non si conosce. E di quando in quando ci sarà qualche simile quantità del secondo costo, la cui merce, cioè il quarto numero ignoto, nuovamente si ignorerà. Perciò, per trovare il numero sconosciuto per mezzo di quelli noti, vi tramandiamo la regola universale, tale in ogni caso, vale a dire scrivi il primo numero nella parte destra, in cima alla tavola, cioè la merce; in fondo alla stessa linea poni il costo della stessa merce, cioè il secondo numero; anche il terzo, se sarà stato merce, scrivilo sotto la merce, cioè sotto il primo; e se sarà stato il costo, scrivilo sotto il costo, cioè sotto il secondo, così tuttavia, come fu del genere dello stesso sotto il quale si deve scriverlo, così sia anche della qualità e della quantità dello stesso in numero, o in peso, o in misura; cioè se il numero superiore sotto il quale si deve scrivere, sarà stato il numero di rotoli allora similmente l’altro sarà di rotoli, se di libbre, di libbre, se di once, di once, se di canne, di canne. E se sarà stato un numero di soldi, che lo stesso sia un numero di soldi, se di denari, di denari, se di tareni, di tareni, e se di bisanti, di bisanti. Scrittili in questo modo, apparirà in modo assai evidente che quei due che si moltiplicheranno assieme saranno sempre posti di traverso; e se si dividerà il totale della loro moltiplicazione per il restante terzo numero, si troverà senza dubbio il quarto numero ignoto: e perché tutto questo si capisca in modo più facile, lo esporremo di seguito con diverse merci e prezzi. |
La regola del tre
A = quantità di una merce a = costo di A B = una seconda quantità della stessa merce A, a, B sono noti, X è il costo della quantità B 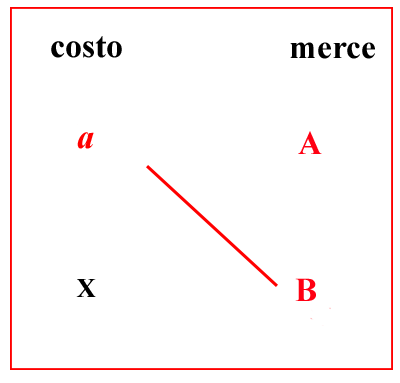
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 Fibonacci e il peso specifico |
(VIII.1.2; G: VIII.7)
Ma prima mostrerò da dove procede questo modo: infatti nei grandi commerci ci sono, come ho detto prima, quattro numeri in proporzione, cioè come il primo sta al secondo, così il terzo sta al quarto, cioè come il numero di una qualche quantità di merce sta al numero della quantità del suo costo, il numero di una qualunque altra quantità della stessa merce sta al numero del suo costo: oppure come una certa quantità di una merce qualsiasi sta a una quantità qualunque della stessa merce, allora nello stesso modo il costo dell’uno sta al costo dell’altro: e quando
(PdA)
le quattro quantità sono così proporzionali, la moltiplicazione della seconda per la terza sarà uguale alla moltiplicazione della prima per la quarta, come è dimostrato in aritmetica e in geometria: per cui se solo la quarta quantità è ignota, essa proviene dalla seconda quantità per la terza, divisa per la prima, appunto dalla divisione: e perciò quando si divide un qualche numero per un qualche numero, e quando dalla divisione ne provenga un altro, se moltiplicherai il numero che ne proviene [il quoziente] per il divisore sicuramente di lì verrà il numero diviso. Ugualmente se non si conosce la terza quantità, la moltiplicazione della prima per la quarta va divisa per la seconda
[NdT]
per tertiam nel testo è un chiaro errore
: e perché tutto ciò che è pertinente ai commerci si abbiano in questo libro in modo eccellente, dividiamo questo capitolo in quattro parti; la prima delle quali sarà sulla vendita dei cantari, e di quelle cose che si vendono a peso o a numero; la seconda in ciò che è pertinente al dazio o al cambio , come il soldo, la lira o la marca d’argento, l’oncia d’oro e cose simili; la terza nelle vendite di canne, balle
[NdT]
Balla (balla) = unità di misura di volume
, di torcelli
[NdT]
Torcello (torscellus)= unità di
Il cum temporale con l’indicativo è talora sostituito al cum narrativo con il congiuntivo [PdA,pag.11]
lunghezza, 1 torcello = 60 palmi e simili la quarta parte sarà nella riduzione dei rotoli di un solo cantaro ai rotoli di un qualunque altro cantaro, secondo la loro diversità. |
A : a = B : X
A : B= a : X
X = a × BA
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Sul cantaro pisano quando viene chiesto il costo dei rotoli, parte prima
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
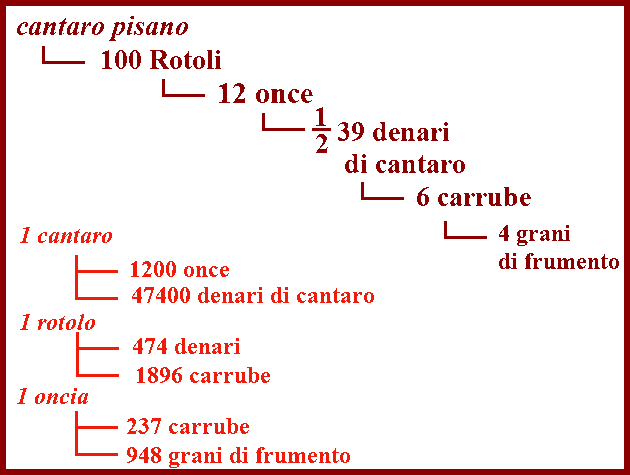
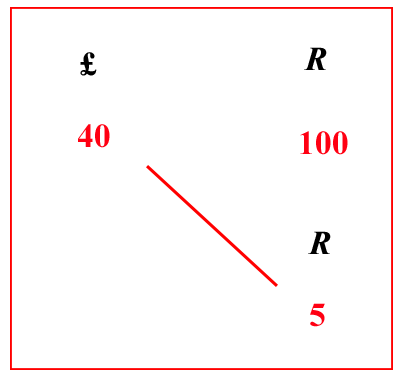
| pg.85 | (VIII.1.3 ; G: VIII.11) Il cantaro pisano
(PdA)
ha in sé cento parti, ciascuna delle quali viene chiamata rotolo; e i rotoli hanno 12 once
[NdT]
In molti casi le medesime unità di misura e di costo si usavano un po’ dovunque, ma il rispettivo valore mutava di paese in paese. Occorreva dunque specificarne l’area geografica di pertinenza con aggettivi come imperialis, pisaninus, ianuinus, turnensi, barcellonensis, saracenatus vel yperperus ecc. [PdA,pag.5]
Secondo l'uso romano l'oncia indica un dodicesimo della grandezza cui si riferisce. Per essere precisi si dovrebbe dire "oncia di rotolo", "oncia di libbra" "oncia di libbra leggera" ecc. Tuttavia quando il contesto non è ambiguo la specifica viene sottointesa.
, ciascuno delle quali pesa 39 denari di cantaro; e un denaro è 6 carrube
(PdA)
, e una carruba è quattro grani di frumento. Questo cantaro si venda per 40 lire; e si chieda quanto valgano 5 rotoli: poiché i tre numeri noti sono già stati posti in questa posizione, [ vedi tabella ], come abbiamo già detto prima che sarebbe stato necessario, cioè rotoli 100, e lire 40, e rotoli 5, dei quali due sono dello stesso genere, cioè rotoli 100 e rotoli 5, perché sono merci. L’altro invece, cioè il 40, è di un altro genere, cioè il costo; ed è il costo dei detti 100 rotoli: perciò, come abbiamo detto prima, si scrivano rotoli 100 e lire 40 in una sola linea, cioè scrivendo all’indietro, poi si scriva rotoli 5 sotto rotoli 100: come si mostra qui più in alto: e ci saranno due numeri di un solo genere, uno sotto l’altro, come abbiamo detto prima, cioè 5 rotoli sotto 100 rotoli: poi, scrittili così, moltiplicherai i numeri che sono di traverso, cioè 5 per 40, farà 200, dividili per 100, farà 2 lire come costo di quei 5 rotoli, e questo 2 si scrive sotto il 40: poiché quel numero che viene dalla divisione, è sempre del genere di quel solo numero, che è nei tre detti numeri: per cui è manifesto che dei quattro numeri che si pongono nel commercio, due di questi sono merci, e gli altri due sono prezzi; e così sono proporzionali, poiché come 100, cioè le merci, sta al suo costo, cioè 40, così 5, cioè le merci, starà al suo costo, cioè a 2. Infatti 100 a 40 è cinque mezzi di essi: similmente anche 5 a 2 sono cinque mezzi di essi. E ancora come 40, cioè il costo, sta a 100, cioè alla sua merce, così 2 starà alla sua merce, cioè a 5: infatti 40 è due quinti di 100, e 2 è due quinti di cinque: anche permutati, così la merce sta alla merce , cioè 5 sta a 100, che è
120 di esso; così il costo sta al costo, cioè 2 a 40: o, come 100 sta a 5, che è il suo ventesimo, così 40 sta a 2; e con queste proporzioni potrai dedurre con giudizio se il quarto numero sarà stato trovato in modo corretto, come sarà dimostrato a suo luogo.
Carruba termine di derivazione araba: : i semi dell’albero del carrubo si usavano per pesare. [PdA,pag.5]
|
  |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Sullo stesso quando si chiedono le merci dalle lire
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
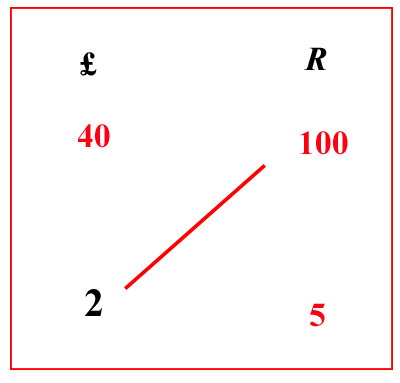
| (VIII.1.4; G: VIII.17) Ugualmente 100 rotoli per 40 lire; quanti rotoli avrò avuto per 2 lire: poiché in questi tre numeri due sono del genere del costo, cioè 40 lire, e 2 lire, e l’altro è del genere delle merci, si scrivano 40 e 100 in una sola linea; poiché si dice 100 rotoli per 40 lire: poi si scrivano 2 lire sotto 40 lire, e saranno numeri dello stesso genere, uno sotto l’altro, come si vede in questa seconda tabella: e moltiplica i numeri che sono di traverso, cioè 100 per 2, farà 200; dividilo per 40, farà 5 rotoli come merce di quelle 2 lire, scrivili sotto i 100 rotoli. |
 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Sullo stesso quando si chiedono i prezzi dei rotoli
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
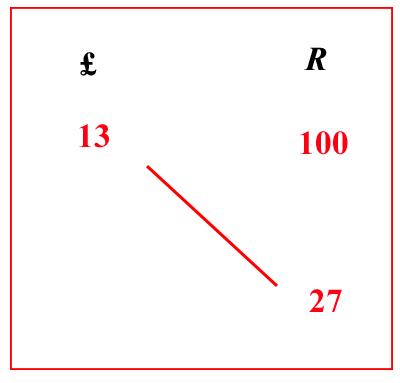
(VIII.1.5 ; G: VIII.19)
Ugualmente un cantaro si vende
(PdA)
per 13 lire; quanto valgono 27 rotoli?
[NdT]
Abbiamo aggiunto il punto interrogativo,
Il verbo vendere e in generale i verbi estimativi, che implicano un valore commerciale, richiedono classicamente l’ablativo del costo: cum te trecentis talentis regi Cotyi vendidisses (Cic. Pis. 84). All’epoca di Leonardo, tuttavia, l’incertezza nell’uso dei casi e la preferenza per sintagmi preposizionali hanno ormai imposto la costruzione vendere aliquid pro aliqua re. [PdA,pag.10]
che non c’è nel testo, solo in questo caso. Nel seguito lasceremo la punteggiatura originaria : si scrivano i numeri, come abbiano detto prima, cioè 100 rotoli e 13 lire su una stessa linea, e 27 rotoli sotto il 100: si moltiplichino i numeri che sono di traverso, cioè 13 per 27, farà 351; dividilo per 100, cioè per 10 1010, farà 15 1010 3 , che scrivi sotto lire 13, come appare in quest’altra descrizione. Infatti se da 15 1010 avrai voluto sapere che parti siano di una lira [NdT] La lira è divisa in 20 soldi e un soldo in 12 denari , moltiplica il 5 che è sopra il 10, per l’altro 10, e aggiungi 1, farà 51; moltiplicalo per il totale dei denari di una lira, cioè per 240, farà 12240; dividilo per 10 1010, farà 4 10122 denari, che sono 10 soldi e 2 52 denari: altrimenti duplica il 5, che è sopra il 10, farà 10, che sono i soldi. Ugualmente duplica l’1 che è sopra l’altro 10, farà 2, che si hanno come denari con altrettanti quinti. Da ciò è quindi chiaro che da una qualunque lira di denari, che sarà stata divisa per 100, vengono 2 52 denari; e da ogni decina di lire 2 soldi, e da singole 5 lire si ha 1 soldo. |
 510 di lira = 1020 di lira, cioè 10 soldi. 1100 di lira = 240100 denari, cioè 2 5 2 denari. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Sullo stesso
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
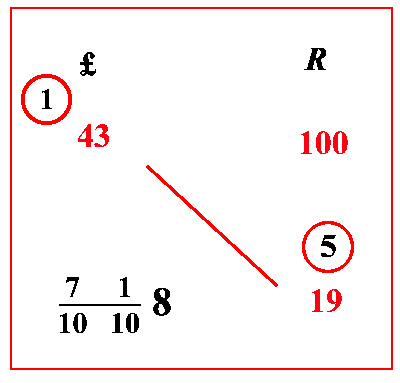
| (VIII.1.6 ; G: VIII.22) Ugualmente, se si vendano 100 rotoli per 43 lire; e si chieda quanto valgano 19 rotoli: scritti questi secondo l’insegnamento prima descritto, moltiplica i numeri che sono di traverso, cioè 19 per 43, farà 817; dividili per 10 1010, farà 71 10108, ponilo sotto libbre 43. Infatti da 71 1010 si conosce che parti sono di una lira, così come abbiamo detto prima. Cioè, quando duplicherai l’uno che è sopra il 10, saranno 2 soldi. Ugualmente duplicherai il 7 che è sopra l’altro 10, saranno 14 denari con altrettanti quinti; uniti questi con i 2 soldi che abbiamo appena avuto, saranno 3 soldi e 4/5 4 denari; e tanto valgono quei 19 rotoli più di 8 lire: possiamo in verità agire in modo più agevole da quel 7, tanto che si prendano 5 dallo stesso 7, per essi tieni 1 soldo, sommalo con i 2 soldi trovati, farà 3 soldi. Duplica quindi la differenza che c’è tra 5 e 7, farà 4 denari con altrettanti quinti, come sono stati or ora trovati. |
 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Sullo stesso
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
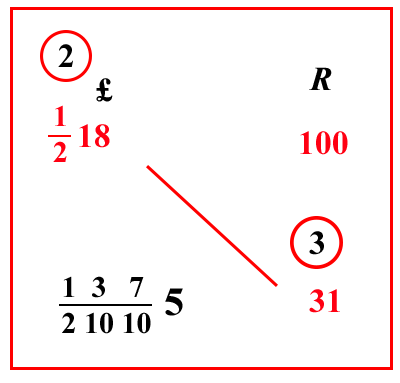
| (VIII.1.7 ; G: VIII.25) Ugualmente 100 rotoli valgono 1 218 lire; quanto valgono dunque 31 rotoli: scritti dunque i numeri in ordine, moltiplica 18 per 2, che sta sotto la linea di frazione prima di esso, e somma l’1 che è sopra il 2, farà 37, ponilo sopra il ; e moltiplica il 37 per il 31 che è di traverso, farà 1147; dividilo per 100, e per il 2, che sta sotto la linea del 18, cioè per 100 21010, farà 137 210105 lire come costo dei richiesti 31 rotoli. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| (VIII.1.8 ; G: VIII.26) Se tutto questo è chiaramente corretto lo si sa attraverso il resto del 7, cioè che tu divida 18 per 7, resta 4; moltiplicalo per 2, e in più aggiungi 1, per l’1 che è sopra lo stesso 2, farà 9; dividilo per 7, rimarrà 2 come resto di 37. Ugualmente prendi il resto per 7 di 31, che è 3; e moltiplicalo per il resto appena trovato di 37, cioè per 2, farà 6, che si serbia come resto del costo dei 31 rotoli: poi moltiplica 5 per il resto di 10, che è posto prima di esso nella linea di frazione, cioè per 3; e in più somma il resto di 7 che sta sopra questo 10, cioè 0, farà 15; dividilo per 7, resta 1; moltiplicalo per il resto del 10 seguente nella linea , cioè per 3, e in più aggiungi 3 che è sopra lo stesso 10, sarà 6; che moltiplichi per 2 che è sotto la stessa linea e in più somma 1, che è sopra il 2, farà 13; dal quale togli 7, rimane il 6, che è stato serbato come resto. In verità se vorrai sapere quante parti di una libra siano 137 21010, moltiplica il 7 che è sopra il 10 per l’altro 10, e in più somma il 3 che è sopra questo stesso 10; e moltiplicalo per il 2 della linea di frazione , e somma l’1 che è sopra il 2, farà 147; moltiplicalo per 240, cioè per il numero dei denari di una lira, farà 35280; dividilo per 137 21010: essendoci poi in questa moltiplicazione lo zero, si divida nella prima posizione di questo per 1 10, cioè si tolga di lì lo zero, resta 3528; dividilo per 10 210, farà 4 10176, che sono 14 soldi, e 2 58 denari. |
 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Sul centone quando se ne chiede il costo partendo dalle lire
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
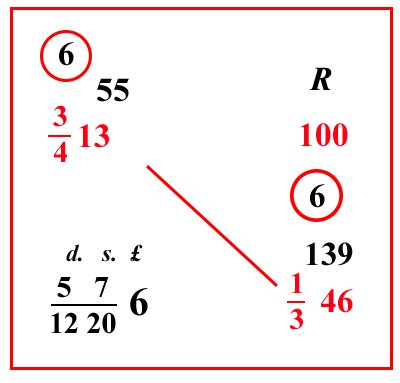
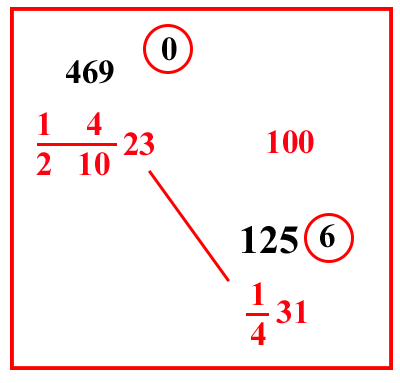
| (VIII.1.9 ; G: VIII.29) E ancora, se un centone di pepe, che pesa 100 libbre sottili, ciascuna delle quali è 12 once, e ogni oncia pesa 25 denari di cantaro; e 158 di queste libbre fanno 1 cantaro, cioè 100 rotoli pisani; si vendano per 3 413 lire; e si chieda quanto valgono 1 346 libbre: si scrivano i numeri, come abbiamo già detto, cioè 100 libbre in una sola linea con 3 413 lire, e 1 346 libbre sotto le 100 libbre, cioè merce sotto merce, come abbiamo fatto prima: e moltiplica i numeri che sono di traverso, cioè 3 413 per 1 346, e dividi per 100, cioè moltiplica 13 per 4, e poi aggiungi il 3 che è sopra il 4, farà 55, che porrai sopra 3 413. Ugualmente moltiplica 46 per 3 e somma 1, farà 139; ponilo sopra 1 346, e moltiplica 55 per 139, farà 7645; dividilo per 100 e per il 3 che è sotto la linea del 46, e per il 4 che è sotto la linea del 13, cioè per 1000 261010; e il totale che ne farà sarà il costo di quelle 1 346 libbre: ma poiché delle frazioni che sono sopra la linea non possiamo sapere che parte o che parti siano di una lira, finché non moltiplichiamo il numero della frazione per i denari, cioè le lire per 240; perciò le frazioni sulla linea della divisione, cioè 1000 261010, devono essere sistemate in altro modo; cioè del 100, valore al quale perviene la divisione, facciamo 10 520: perché quello è la stessa cosa che 10 1010, e di 1 3 e di 1 4 scritti prima facciamo solo 1 12 ; e si ponga in una linea di frazione, così 100 51220 che è lo stesso di 1000 261010, dividi 7645 per questo 100 51220; e ciò che rimarrà oltre il 20 saranno i denari, poiché una lira di denari è 20 soldi, e ciò che sarà uscito oltre il 12 saranno denari. Questo perché un soldo è 12 denari; e ciò che sarà rimasto oltre le altre frazioni, indicherà solo le parti di un unico denaro: per cui se avrai diviso 7645 per 100 51220, farà 057 512206 lire come costo delle dette 1 346 libbre; che è tanto, quanto se per il nominato si dicesse 6 lire e 7 soldi, e 5 denari. In verità, se 10 1220 non possono essere disposti tra i numeri dai quali si ha la divisione, chiariremo nei seguenti problemi in che modo allora si dovrà fare: ma ci occupiamo di mostrare in che modo tutti i numeri si dividano facilmente per 12 e per 20. In verità tutti i numeri possono essere divisi per 12, nello stesso ordine in cui abbiamo insegnato a dividere numeri per numeri che vanno dal due fino al nove. Quindi devono essere imparate le divisioni di qualche numero per 12; così da 12 diviso in primo luogo per 12, fa 1, da 24 fa 2, da 36 fa 3, da 48 risulta 4, da 60 fa 5, da 72 fa 6, da 84 fa 7, da 96 fa 8, da 108 fa 9, come è contenuto nella tavola delle divisioni. |
 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| (VIII.1.10; G: VIII.37-38) Inoltre quello che sarà avanzato di un qualunque numero a destra o a sinistra di 120, è quello che dobbiamo scrivere nelle divisioni dei numeri sopra quel numero di cui sarà l’avanzo e unirlo con la cifra precedente che sta nel numero da dividere. Per esempio se volessimo dividere 3479 per 12, si scriva il 12 sotto il 79 del 3479 e si prenda la dodicesima parte di 34, che è 2, e resta 10; e questo è l’avanzo che c'è tra 24 e 34: e poni il 2 sotto il 4 di 34 e il 10 sopra lo stesso 34, a questo 10 aggiungi il 7, cioè la cifra antecedente, farà 107; dividilo per 12, farà 8 e resta 11, cioè la differenza che c'è da 96 fino a 107: poni dunque l'8 sotto il 7, e l'11 sopra il 107, cioè l'1 sopra lo 0 e l' 1 sopra il 7 e unirai questo 11 con il 9 che lo precede, farà 119 dividilo per 12, farà 9 e resta 11: poni il 9 sotto il 9 e l'11 in qualche altra parte sopra il 12 , e avrai per la richiesta divisione 11 12 289, come si vede in figura. Perciò è chiaro che 3479 denari sono 289 soldi e 11 denari, poiché quando una qualche somma di denari viene divisa per 12, allora da tale divisione fanno i soldi: e se le cose che sono state dette sulla divisione per 12 le rinforzerai scrivendole ripetutamente sulla tavoletta con impegno, con queste nella mente e nelle mani, potrai molto facilmente operare. | Esegue la divisione per 12 oltre il 120.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
La divisione dei numeri per 20
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| (VIII.1.11 ; G: VIII.41) Dunque tutti i numeri li possiamo dividere per 20 in questo modo: lascia da parte la figura di prima posizione del numero che vuoi dividere e sotto la seguente, cioè sotto la figura di seconda posizione del medesimo numero, poni il 2 per il quale dividi tutto il numero fino alla figura stessa sotto la quale è posto il 2; e ciò che farà dalla divisione sarà 1 20 di tutto il numero che avrai voluto dividere: e se avanzerà qualcosa uniscilo con la figura in prima posizione che abbiamo richiesto di lasciare da parte, e ciò che farà dall'unione è quello che resterà della suddetta divisione: e se sopra la seconda figura non ci sarà nulla, allora solo la prima figura sarà il resto. Per esempio: se avremo voluto dividere 1234 per 20, si lascino da parte il 4 che sta in prima posizione e si ponga il 2 sotto la figura successiva, cioè sotto il 3, si ponga il 2; per il quale si divida il 123 che resta da 1234; sottratto di lì il 4, farà 61, e resta 1, che, unito con il 4, fa il 14: dunque dalla divisione di 1234 per 20 viene 61 col resto di 14, come qui si mostra: da ciò infatti è chiaro che 1234 soldi sono 61 lire e 14 soldi. Mostrate pertanto le divisioni per 12 e per 20, ora invero torniamo ai nostri propositi |
Divisione per 20
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Sul centenario massamutino
[NdT]
In documenti del 12° e 13° sec., nome
con cui è indicato il bisante d’oro; deriva forse dall’arabo masmūdī, moneta coniata in Spagna dagli Almohadi, originari della tribù dei Uaṣmūda |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| (VIII.1.12 ; G: VIII.44) 100 massamutini valgono 1 253 lire; quanto valgono dunque 1 923 massamutini: scrivi i numeri in ordine, così come è stato detto più sopra, e moltiplica i numeri che sono in traverso, cioè 1 253 e 1 923, e dividili per 100, cioè moltiplicherai il 53 per la sua frazione, farà 107, ponilo sopra 1 253. Ugualmente moltiplicherai 23 per il 9 e in più sommerai l'1, farà 208; ponilo sopra 1 923, e moltiplica 107 per 208, farà 22256; dividilo per 100, e per 2 e per il 9 che sono sotto le linee di frazione, cioè per 1000 291010, e avrai il costo di quei 1 923 massamutini: oppure unisci i numeri della divisione, così che tu possa avere in cima alla linea di frazione 10 1210, perché tu abbia in un’unica moltiplicazione lire, e soldi, e denari, come abbiamo fatto nel precedente problema, cioè affinché tu di 10 1010 faccia 10 520; e poiché non possiamo unire in 1 12 le frazioni residue della divisione, cioè 1 2 e 1 9, allora prendiamo ciò che da esse possiamo prendere della composizione del 12, cioè dalla regola del 9 dobbiamo prendere 1 3, e congiungere quello stesso 1 3 con 1 2, fanno 1 6. L'altro numero che ci manca del 12, cioè il 2, lo dobbiamo moltiplicare per 22256, farà 44512; dividilo per 1000 351220, farà 1237 35122012 come costo di 1 923 massamutini: |
Si vuole avere nel denominatore
della frazione 222562×9×10×10 12 e 20 per poter dividere il risultato in soldi e denari. 2×9×10×10 = 3×5×6×20 moltiplicando numeratore e denominatore per 2 abbiamo: 222562×9×10×10 = 445123×5×12×20 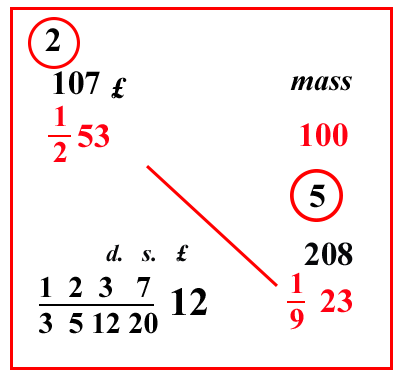 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
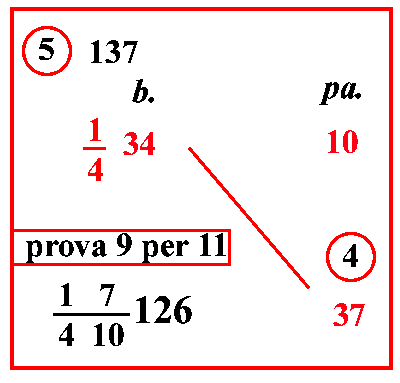
| (VIII.1.13 ; G: VIII.47) Se vorrai verificarlo con la prova del 7, prendi il resto di 53, che è 4; e moltiplicalo per il 2 della linea di frazione e somma l'1, farà 9; prendine il resto, che è 2; e tanto deve essere il resto di 107, e così è: poi prendi il resto del 23 che è 2 e moltiplicalo per il 9 della frazione e somma l'1, farà 19; il cui resto, cioè 5, è il resto del 208: moltiplicalo per il resto di 107, cioè per 2, farà 10, moltiplicalo per il 2 che abbiamo tolto dalla scomposizione del 12, cioè per il 2 per il quale abbiamo moltiplicato il 22256, farà 20; da cui prendi il resto, che è 6, e conservalo come resto di 1237 35122012: e se sarà stato altrettanto per tutti gli altri, sappi di aver proceduto correttamente: e si prende il loro resto così: si moltiplica il resto del 12, che sta fuori la linea di frazione, per il resto del 20 che sta sotto la linea di frazione, cioè 5 per 6, fa 30; a cui si somma in più il 7, che sta sopra il 20, farà 37; il cui resto, cioè il 2, si moltiplica per 5, cioè per il resto di 12 e si somma il 3, che sta sopra il 12, farà 13, il cui resto, cioè 6, si moltiplica per 5, e si somma sopra in più il 2, che sta sopra il 5, farà 32; moltiplica il suo resto, che è 4, per il 3 della linea di frazione, e in più aggiungi l’1che sta sopra il 3, fanno 13, il cui resto è 6, come è stato conservato come prova. E così sempre quando vorrai trovare il resto di qualunque problema simile, a seconda di come vai moltiplicando, così impegnati a andare avanti facendo la prova con qualsiasi resto, finché sarai arrivato all'ultima moltiplicazione: e avuto il resto dell'ultima moltiplicazione, conservalo come prova del risultato della divisione; e ciò che è stato detto sulla prova, riteniamo sia abbastanza sufficiente per gli altri problemi. |
Esegue la prova del 7
Il resto in diagonale è 2×5×2 perché abbiamo moltiplicato per 2 per avere 12 nei denominatori. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Sulle cento pelli.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
pg.89 |
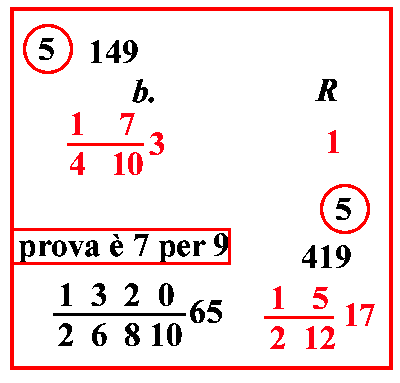
(VIII.1.14 ; G: VIII.51) Se 100 pelli valgono 1 93 583 lire, quanto valgono 32 pelli: scrivi i numeri, e moltiplica 1 93 583 per 32 poiché sono posti di traverso, e dividi la loro moltiplicazione per 100, cioè moltiplica 83 per le sue frazioni, farà 3767: ponilo sopra 1 93 583, e verificalo con qualunque prova tranne quella del 9: poi moltiplica 3767 per 32, farà 120544, dividilo per 100 e per 10 59, e sistemalo in modo da avere 10 1220 all'inizio della linea di frazione: così di 100 fai 10 520, e di 1 9 fai 10 33; e da quest'ultimo prendi 1 3 e lo moltiplicherai per 4; così fa 12, e poni quel 12 davanti al 20, come più sopra abbiamo mostrato di fare; e sistema le altre frazioni davanti a 10 1220, e avrai sulla linea di frazione della divisione 10000 3551220: e poiché si toglie 1 4 da questo 12, poni il 4 sopra il 100 perché tu lo abbia affidato più saldamente in memoria, quando troverai la prova, e moltiplicalo per quel 120544, farà 482176; dividilo per 10000 3551220, farà 100915 355122026 come costo di quelle 32 pelli, come si vede più sopra nel riquadro. |
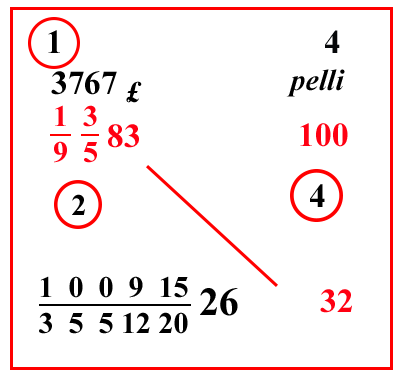 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
(VIII.1.15 ; G: VIII.54)
Ancora 100 rotoli valgono
1
71
423 lire; quanto valgono dunque
23
51364 di rotolo. Scrivi il problema, e moltiplica il 23 per le sue frazioni, farà 655; ponilo sopra il 23, e fai la prova con il resto, se la moltiplicazione è corretta: poi moltiplica il 64 per la sua frazione, farà 4177; e moltiplicalo per 655, farà 2735935, che non trascurerai di verificare bene; e dividilo per il numero 100, e per le frazioni di entrambi i numeri che sono posti di traverso, naturalmente sistemate insieme nel migliore dei modi; così da avere all'inizio della linea di frazione
10
1220, e tu devi fare così: del 100 fai
10
520; vedi se potrai sottrarre qualcosa dalle altre frazioni della divisione, per avere il 12 o una qualche parte di esso; da esso soltanto puoi avere solo
1
4 delle parti del 12, cioè della sua composizione: dunque sottraiamo 3 così avremo il 12 sulla linea di frazione davanti al 20: perciò poni il 3 sopra il 100, come si mostra nel riquadro, così da tenerlo più tenacemente in memoria, e sistema i numeri che restano della divisione davanti a
10
1220 così:
100000
557131220 ; e moltiplica il 2735935 per il 3 serbato sopra il 100, farà 8207805; di nuovo verificalo con il resto, e dividilo per
100000
557131220, farà
0151070
55713122015 come costo dei rotoli richiesti; ed il resto di questo [ che è 3 ] per il resto di 100
[NdT]
Nel testo manca una parte che abbiamo ricostruito noi è 3, come si vede sopra nel riquadro. |
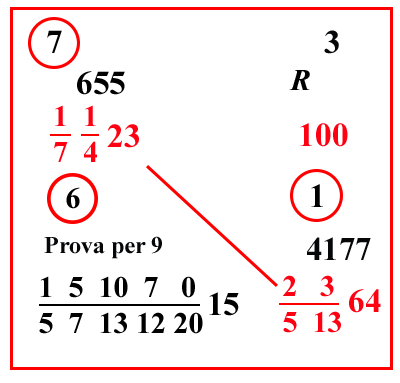
Il denominatore del risultato contiene un 5 in meno e un 3 in più rispetto al prodotto in diagonale.
I resti 7×1×3 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Sul cantaro
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| (VIII.1.16 ; G: VIII.57) Ugualmente un cantaro di una merce qualsiasi vale 14 lire e 7 soldi; quanto valgono dunque 37 rotoli della stessa merce: fai dei soldi 7 parti di una lira, farà 7 20, ponili davanti al 14 così: 7 2014; e scrivi il problema, e moltiplica 7 2014 per il il 37 che è di traverso, e dividi per 100, cioè moltiplica il 14 per 20 e in più somma il 7 che sta sopra il 20, farà 287 soldi; ponili sopra il 7 2014, e moltiplicali per 37, farà 10619, che devi dividere per 100 e per il 20 della frazione, ma poiché occorre per noi avere il 12 sulla linea di frazione della divisione, per avere in una sola moltiplicazione le lire e i soldi e i denari, moltiplica 10619 per questo 12 e dividilo per 100 e per 10 1220, cioè per 1000 10101220, farà 8226 101012205 lire come costo dei detti 37 rotoli, la cui prova del 9 è 6. |
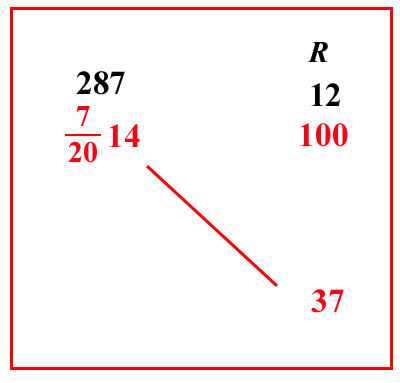 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Sul centone di panni.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
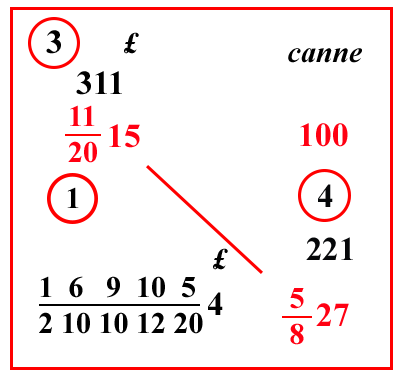
(VIII.1.17 ; G: VIII.59)
Ugualmente 100 canne di panni valgono
11
2015 lire, quanto valgono dunque
5
827 canne, cioè 27 canne e
1
22 braccia
[NdT]
Una canna equivale a 4 braccia
; scritto perciò il problema, moltiplica il 15 per il 20 e somma l'11, farà 311 soldi, ponili sopra il 15. Ugualmente moltiplica il 27 per l'8 e somma il 5, farà 221; ponilo sopra il 27, e moltiplica il 311 per il 221, farà 68731, che dobbiamo moltiplicare per 12 per averlo nella linea di frazione, se non che abbiamo nella divisione l'8, cioè quello che sta sotto la linea di frazione davanti alle 27 canne, la cui regola è
10
28: perciò triplicheremo il 4 e avremo il 12 nella divisione. Poi si moltiplichi lo stesso 68731 per 3; perché quando si triplica il divisore, si deve triplicare anche il dividendo, farà 206193; dividilo per il 2 che resta dalla regola dell'8, una volta tolto di lì il 4, e per 100 e per 12 e per 20, cioè per
10000
210101220, farà
169105
2101012204 lire, il cui resto per 7 è 1, come si vede in questo riquadro
[NdT]
110 braccia e mezzo di panni, se l’esempio è realistico, costavano
.
4 lire 5 soldi e 10 denari |
 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Sul centone di pepe
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
pg.90 |
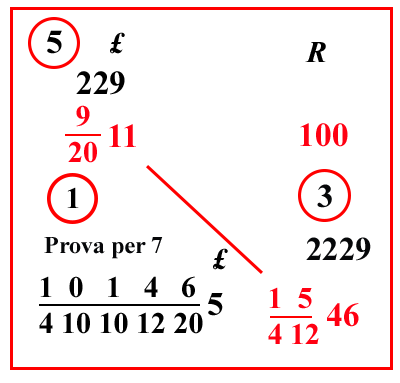
(VIII.1.18 ; G: VIII.62)
Ugualmente un centone [ 100 libbre ] di pepe vale
9
2011 lire: quanto valgono quindi
15
41246 libbre, cioè 46 libbre e
1
45 once: scrivi il problema, e moltiplica l'11 per 20
[NdT]
205 nel testo è un chiaro errore
e somma il 9, farà 229 ponilo sopra l'11. Ugualmente moltiplica il 46 per il 12 e somma 5, e moltiplica per 4 e somma 1, farà 2229; ponilo sopra il 46, e moltiplica 229 per il 2229, farà 510441; dividilo per 100 e per 20, e per
10
412, cioè per
10000
410101220, farà
10146
2101012205 lire come costo di quelle
15
41246 libbre, la prova del sette è 1
|
 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
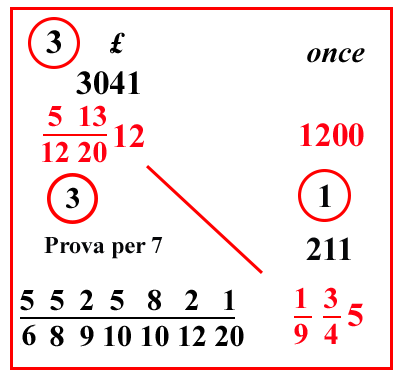
| (VIII.1.19; G: VIII.64) Ugualmente un centone vale 12 lire, e 13 soldi, e 5 denari, cioè 513 122012 lire: quanto valgono allora 1 93 45 once: sebbene in questo problema le 100 libbre e le 1 93 45 once siano del genere della mercanzia, tuttavia non sono dello stesso peso perché 100 sono libbre e sono once: per questo bisogna fare le once da 100 libbre, saranno1200; e allora saranno entrambe simili, e questo problema sarà così: poiché 1200 once valgono 513 122012 lire, quanto valgono allora 1 93 45 once: scrivi questo problema come abbiamo insegnato, e moltiplica il 12 per la sua frazione, farà 3041 denari, ponili sopra le 12 lire. Ugualmente moltiplica il 5 per la sua frazione, farà 211, ponilo sopra 1 93 45; e moltiplica 211 per 3041, farà 641651; dividilo per 1200, e per 4, e per 9, e per 10 1220 sistemati nel modo migliore in una sola linea di frazione, farà 5525821 68910101220 come costo delle once richieste, come si vede in questo riquadro. |
 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Sul cantaro
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
(VIII.1.20; G: VIII.67)
Ugualmente un cantaro vale
1716
4122021 lire; e si chiede quanto valgano
127
7512
43 rotoli, cioè 43 rotoli e
1
72
57 once
[NdT]
1 cantaro = 100 rotoli ,
. Quindi, scritto il problema, moltiplica il 21 per la sua frazione, farà 20957. Ancora moltiplica i 43 rotoli per 12 e somma 7; e moltiplica per 5, e somma 2; e per 7, e somma al risultato la moltiplicazione di 1 che è sopra il 7 per il 5, farà 18324; moltiplicalo per 20957, farà 384016068; dividilo per 100 e per le frazioni che sono sotto le linee di frazione di entrambi gli altri numeri, sistemate naturalmente nel migliore dei modi, farà
037908510
37810101012209 come si vede in questo riquadro, la cui prova dell'11 è 7.
1 rotolo = 12 once |
Ricordiamo che
127 7512 = 7 12 + 1 12⎧⎩2 5 + 1 7⎫⎭ 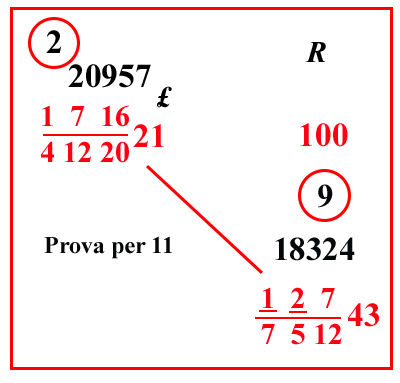 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Sul cantaro venduto per lire e denari.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| (VIII.1.21; G: VIII.69) Ugualmente un cantaro vale 13 lire e 7 denari, cioè 70 122013 lire; quanto vale quindi 7 cantari, e 43 rotoli, cioè 743 rotoli: scrivi il problema, e moltiplica il 13 per il 20; e per il 12 e somma il 7, farà 3127; moltiplicalo per 743, farà 2323361; dividilo per 100, e per 10 1220, cioè per 1000 10101220, farà 16116 1010122096 come costo dei 743 rotoli. |
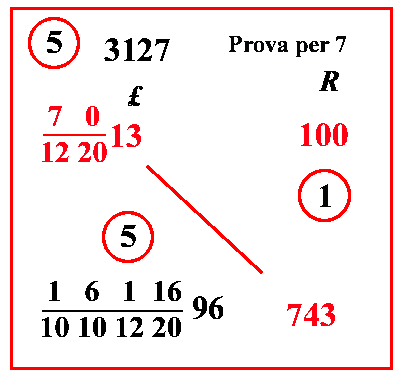 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Sul migliaio venduto per lire e soldi.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| (VIII.1.22 ; G: VIII.70) Ugualmente un migliaio di merci varie è venduto per 153 lire e 9 soldi, cioè per 920153 lire; quanto valgono dunque 227 merci varie: scrivi il problema, e moltiplica 153 per la sua frazione, farà 3069; moltiplicalo per 227, farà 696663; moltiplicalo per 12 per averlo nella linea di frazione della divisione, farà 8359956; dividilo per la regola di 1000 e per 10 1220, cioè per 10000 1010101220, farà 659716 101010122034 lire come costo delle varie merci richieste. | 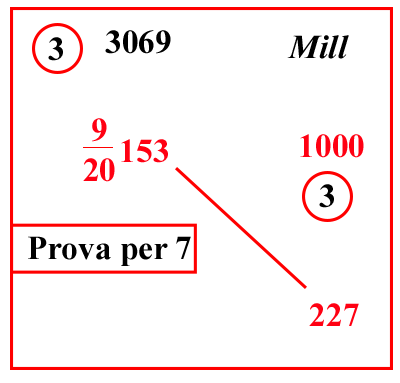 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Sullo stesso argomento per lire e soldi e denari.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| (VIII.1.23 ; G: VIII.71) Ugualmente 1000 rotoli sono venduti per 58 122057 lire; quanto valgono quindi 5687 rotoli: scritto così il problema, moltiplica il 57 per la sua frazione, farà 13781, ponilo sopra il 57. Ugualmente moltiplica l'87 per 6 e somma 5, farà 527; moltiplicalo per 13781, farà 7262587; dividilo per 1000 e per le frazioni dei numeri che restano, cioè per 100000 61010101220, farà 1134100 610101012205 lire. |
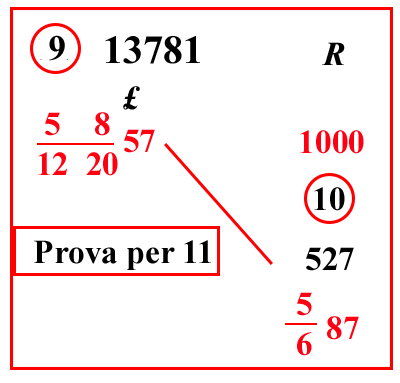 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Sul peso pisano di formaggio.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
pg.91 |
(VIII.1.24; G: VIII.72)
Un peso
[NdT]
La parola Pondus è tradotta
di formaggio, che pesa 22 centoni, cioè 2200 libbre, è vendutoda Sigler con Ton (tonnellata)
(PdA)
per 24 lire; si chiede quanto valgano 86 libbre: scrivi il problema, e moltiplica 24 per 86, farà 2064; dividilo per la regola di 2200, cioè per
1000
2101011; tuttavia fa
120 di
10
210, affinché lo si abbia nella frazione così
100
101120: e poiché non abbiamo il 12 in questa divisione, si moltiplichi il 2064 per 12, e si ponga il 12 sotto la linea di frazione della divisione. Poiché quando si aggiunge il 12 sotto la linea di frazione della divisione, allora si moltiplica il divisore per 12: perciò si deve moltiplicare similmente il numero da dividere per 12, affinché la proporzione tra il dividendo e il divisore sia la stessa che era prima e da ciò abbiamo
81918
10111220.
Il verbo vendere e in generale i verbi estimativi, che implicano un valore commerciale, richiedono classicamente l’ablativo del costo: cum te trecentis talentis regi Cotyi vendidisses (Cic. Pis. 84). All’epoca di Leonardo, tuttavia, l’incertezza nell’uso dei casi e la preferenza per sintagmi preposizionali hanno ormai imposto la costruzione vendere aliquid pro aliqua re. [PdA,pag.10]
|
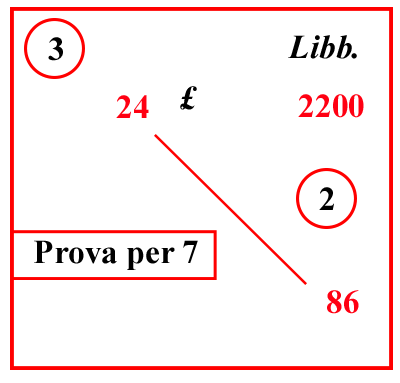 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Sullo stesso argomento
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
(VIII.1.25 ; G: VIII.74)
Ugualmente un peso di formaggio, cioè 2200 libbre, vale
112018 lire; quanto valgono quindi 100 libbre: non è necessario di scrivere questo problema: poiché 100 è
122 di 2200: per questo motivo non c'è bisogno di altro, se non che si divida il detto costo del peso per la regola del 22, cioè per
10
211, che puoi fare così: prendi
12 delle 18 lire, e 11 soldi, farà 9 lire e
125 soldi; di cui fai soldi, saranno 185 soldi e 6 denari; dividili per 11, farà 16 soldi e restano 9 soldi e 6 denari da
(PdA)
dividere per 11; di questi fanne denari, saranno 114 denari; dividili per 11, saranno
41110 denari; e tanto vale un centenario di formaggio, cioè 16 soldi e
41110 denari.
Spesso ad + acc. del gerundio assume anzi un valore consecutivo, simile a quello che in italiano ha l’infinito preceduto dalla preposizione da. [PdA,pag.12]
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Sullo stesso per le libbre
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| (VIII.1.26 ; G: VIII.76) Ugualmente un peso vale 132019 lire, quanto valgono quindi 783 libbre: scrivi il problema, e moltiplica 19 per 20 e somma il 13, farà 393 soldi moltiplicalo per 783, farà 307719 che devi dividere per la regola di 2200 e per il 20 che è sotto linea di frazione, cioè per 10000 210101120: ma per avere il 12 nella frazione, moltiplica il 307719 per 6, il quale 6 lo unirai con il 2 che sta nella linea di frazione, e avrai il 12 nella frazione stessa, così 10000 1010111220, farà 4151019 10101112206 [ lire ]. |
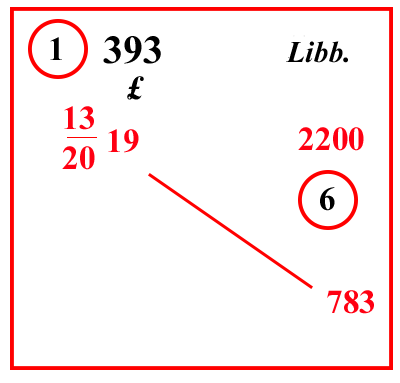 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Sulla carica
(PdA)
di Provenza.
Nella Lex Salica e nelle Leges Visigothorum (sec. VI d.C.) fa la sua comparsa il verbo carricare (e la forma sincopata carcare), costruito su carru con l’aggiunta del suffico -ico. Da car(r)icare derivano i sostantivi car(r)icum e car(r)ica, che Leonardo usa con grafia scempia (cioè con una sola c) rispettivamente per indicare il carico di una nave e un quantitativo di merce, ancora una volta variabile a seconda dei paesi. [PdA,pag.7]
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| (VIII.1.27 ; G: VIII.77) Una carica di Provenza che pesa 300 libbre si vende per 15 lire e 7 soldi, cioè per 72015 lire; si chiede quanto valgano 86 libbre: moltiplica il 15 per 20, e somma il 7, farà 307; ponilo sopra il 15, e moltiplicalo per 86, farà 26402; dividilo per 300 e per 20, cioè per 1000 551220, farà 2008 5512204 lire come costo delle richieste 86 libbre, come qui si mostra. Così infatti devi impegnarti a trovare le regole dei numeri, con i quali si giunge alla divisione, così come facemmo per il 300: sebbene la sua regola sia 100 31010, tuttavia abbiamo posto che essa sia 100 5512 , come abbiamo 112, così abbiamo 120, cioè quello che è col 15. | 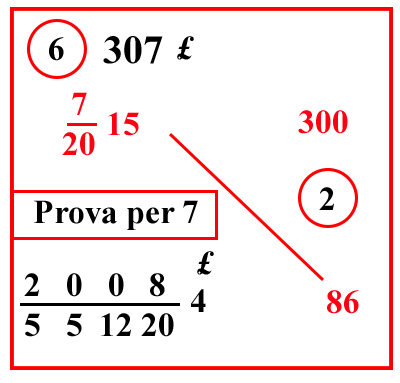 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Sulla stessa carica
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| (VIII.1.28 ; G: VIII.79) Ugualmente una carica di pepe vale 11 lire e 7 soldi e 5 denari, cioè 57 122011 lire; quanto valgono allora 127 libbre, e 1514135 once , cioè 1115 54312 127: scrivi il problema, e moltiplica l'11 per la sua frazione, farà 2729, ponilo sopra l'11. Ugualmente moltiplica il 127 per le sue frazioni, cioè per 12 e somma 5, e per 3 e somma 1, e per 4, e per 5, farà 91760. Ugualmente moltiplica l'1 che è sopra il 4 per il 5, moltiplica il risultato per il 3, farà 15. Di nuovo moltiplica l’1 che è sopra il 5, per 4; e per 3, farà 12, sommalo col 15 e col 91760, farà 91787; ponilo sopra il 127, e moltiplicalo per 2729, farà 250488723; dividilo per la regola di 300, e per tutti i rotti, farà 166066716 38910101012204 come costo di quelle libbre richieste. |
Ricordiamo che
1115 54312 = 5 12 + 1 12⎧⎩1 3 + 1 4 + 1 5⎫⎭ 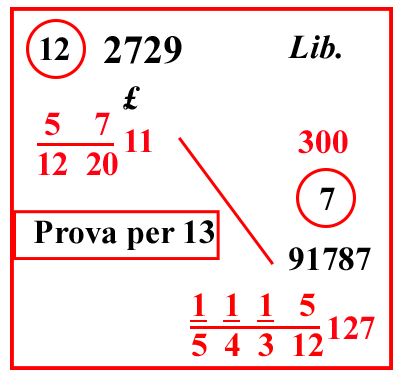 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Sui rotoli
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
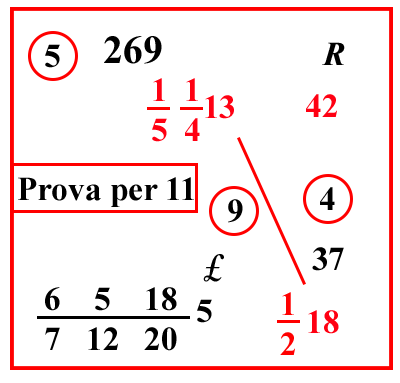
| pg.92 | (VIII.1.29 ; G: VIII.81) Ancora, 37 rotoli valgono 11 lire, quanto valgono allora 18 rotoli: moltiplica l'11 per il 18 farà 198 moltiplicalo per 12 e per 20, cioè per 240, per averli nella frazione, farà 47520; dividilo per 100 371220, farà 1207 3712205 lire come costo dei 18 rotoli. |
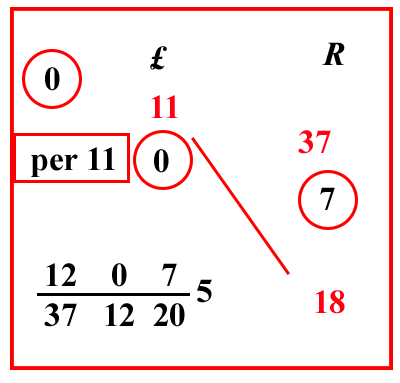 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Sullo stesso argomento.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| (VIII.1.30; G: VIII.82) Ugualmente 42 rotoli valgono 151413 lire; quanto valgono allora 1218 rotoli: moltiplica 13 per le sue frazioni, farà 269; e moltiplica 18 per 2 e somma l'1, farà 37; moltiplicalo per 269, farà 9953; dividilo per la regola di 42, cioè per 10 67 e per il 2, e per il 4, e per il 5, che sono sotto le linee di frazione di entrambi i numeri, sistemandoli in modo tale che di 12 e 16 farai 112, e di 14 e 15 farai 120; e avrai nella loro aggregazione 100 71220, avremo 6518 712205 lire come costo di quei 1218 rotoli. Ora è stato detto abbastanza sia sulla vendita dei cantari e degli altri diversi pesi per le lire di denari, per i quali abbiamo bisogno di avere 10 1220 nelle frazioni di queste divisioni, per avere lire, soldi e denari in una moltiplicazione: adesso di quelle vendite fatte dai soldi, nelle quali avremo bisogno di avere solo 112 all'inizio delle frazioni di quelle divisioni poiché ciò che avanzerà dalla divisione sopra il 12, saranno denari, mentre ciò che dalle divisioni sarà fuori dalla linea di frazione, sono i soldi. |
 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
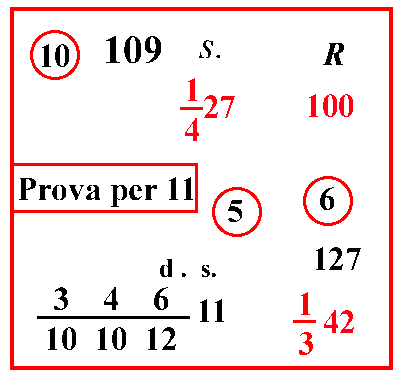
Sul cantaro venduto per soldi e rotti
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| (VIII.1.31; G: VIII.84) Ugualmente i cantari valgono 1427 soldi, cioè 27 soldi e 3 denari; quanto valgono allora 1342 rotoli: moltiplica il 27 per i 4 e somma l'1, farà 109. Ugualmente moltiplica il 42 per 3 e somma l'1, farà 127; moltiplicalo per 109, farà 13843; dividilo per 100, e per 3, e per 4, cioè per 100 101012, farà 346 10101211 soldi. |
 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Sullo stesso per soldi e denari
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| (VIII.1.32 ; G: VIII.85) Ugualmente un cantare vale 26 soldi e 5 denari, cioè 51226 soldi; quanto valgono allora 5831 rotoli: moltiplica il 26 per 12 e somma il 5, farà 317 denari. Ugualmente moltiplica 31 per 8 e somma il 5, farà 253; moltiplicalo per 317, farà 80201 [NdT] 80221 è un chiaro errore ; dividilo per 1000 8101012, farà 1524 81010128. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
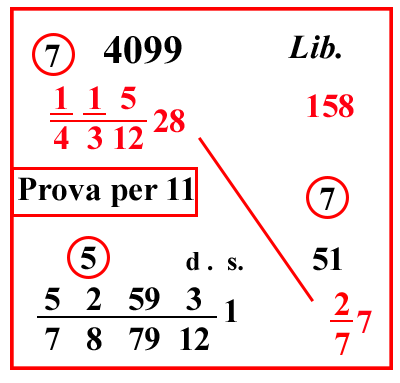
Sullo stesso per soldi e denari e rotti
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| (VIII.1.33 ; G: VIII.86) Ugualmente i cantari, cioè 100 rotoli, valgono 115 4312 28 soldi, cioè 28 soldi e 14135 denari; quanto valgono allora 277 libbre: sebbene 100 rotoli e le 277 libbre siano dello stesso genere, tuttavia non sono della stessa qualità o peso; perché 100 sono rotoli, e 277 sono libbre: perciò o delle 277 libbre sono da farne rotoli, o dei 100 rotoli sono da farne libbre, così come sono di uno stesso genere, così siano di una sola quantità, cioè di un solo peso: che siano entrambi rotoli, o libbre facciamo allora libbre dai 100 rotoli; e saranno 158 libbre pisane: ma le altre sono 150 libbre, che si pongano nel riquadro come costo di vendita: poi moltiplica il 28 per la sua frazione, farà 4099. Ugualmente moltiplica il 7 per il 7 e somma 2, farà 51; moltiplicalo per 4099, farà 209049; dividilo per 158, e per le frazioni, che sistemate insieme fanno 10000 3787912, farà 052593 37879121 soldi: oppure moltiplica soltanto la terza parte di 51, cioè 17 per 4099, e toglierai 3 dalla frazione; perché sempre in tutti i problemi nei quali finiscono la moltiplicazione e la divisione, devi osservare il suddetto modo di semplificare. |
 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
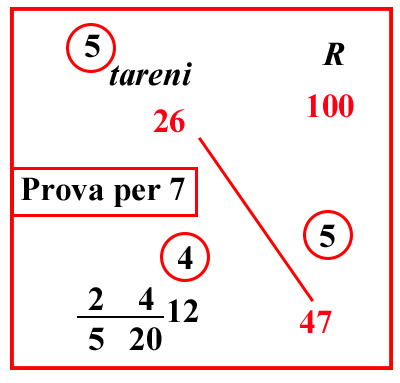
Sul cantaro venduto per tareni
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
pg.93 |
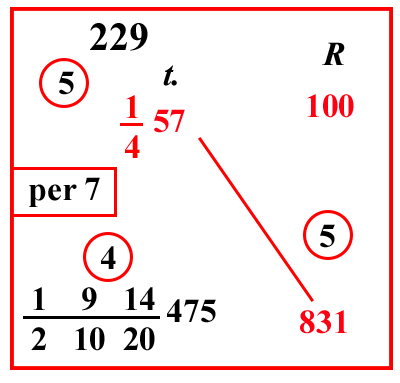
(VIII.1.34; G: VIII.89)
Se il cantaro di una merce qualunque si venda in Sicilia per 26 tareni
[NdT]
Il Tareno è una moneta d’oro araba molto diffusa in Sicilia divisa in 20 grani
; si chieda quanto valgano 47 rotoli: scrivi il problema, e moltiplica i numeri che sono di traverso, cioè 26 per 47, farà 1222, dividilo per la regola di 100, sistemandola in modo da avere di lì
120 all'inizio della linea di frazione; poiché un tareno vale 20 grani; e ciò che sarà rimasto sopra il 20 saranno i grani. Pertanto la regola del 100 è
10
520, se per essa hai diviso 1222, ne verranno
24
52012 tareni, cioè 12 tareni e
254 grani: o altrimenti, poiché hai 1222 nel totale della moltiplicazione, prendi 12 tareni per il 1200; poiché 1200 è cento volte 12: poi ciò che resta, cioè 22, dividilo per 5; e ciò che viene dalla divisione, cioè
254, sono i grani, come abbiamo appena trovato.
|
 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Sullo stesso
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
(VIII.1.35 ; G: VIII.91)
Ugualmente un cantaro si vende
(PdA)
per
1457 tareni: quanto valgono allora 831 rotoli, cioè 8 cantari e 31 rotoli: moltiplica dunque 57 per 4 e somma l'1, farà 229; moltiplicalo per 831, farà 190299: dividilo per 100, e per 4, cioè per
100
4520, o per
100
21020, che è più bello, farà
1914
21020475 tareni, questi 475 tareni sono tareni del peso di Messina
[NdT]
Il verbo vendere e in generale i verbi estimativi, che implicano un valore commerciale, richiedono classicamente l’ablativo del costo: cum te trecentis talentis regi Cotyi vendidisses (Cic. Pis. 84). All’epoca di Leonardo, tuttavia, l’incertezza nell’uso dei casi e la preferenza per sintagmi preposizionali hanno ormai imposto la costruzione vendere aliquid pro aliqua re. [PdA,pag.10]
Il tareno è anche una misura di peso
; e se viorrai sapere quante once sono, dividi questi 475 tareni per 30, poiché 30 tareni qui fanno 1 oncia, avremo
5615 once. Ugualmente se questi 475 saranno del peso di Palermo, dividi 475 per
1327, poiché un'oncia di Palermo è
1327 di tareno.
|
 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Sullo stesso
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
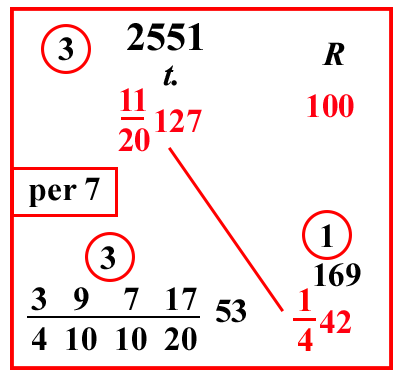
| (VIII.1.36 ; G: VIII.93) Ugualmente un cantaro si vende per 1120127 tareni, cioè per 127 tareni e 11 grani; quanto valgono allora 1442 rotoli: moltiplica 127 per 20 e somma l'11, farà 2551. Poi moltiplica 42 per 4 e somma l'1, farà 169; moltiplicalo per il 2551, farà 431119; dividilo per 100, e per 4, e per 20, farà 39717 210102053 tareni. |
 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
(VIII.1.37 ; G: VIII.94)
Ora è stato detto abbastanza sulla vendita per tareni, adesso trattiamo della vendita delle merci per bisanti di Garbo
[NdT]
Il bisante di Garbo è l'unità di misura monetaria usata dalla popolazione dei Garbi (vedi nota successiva); un bisante di Garbo è diviso in 10 miliari.
, ciascuno dei quali è 10 miliari: per questo è necessario che per essi abbiamo sempre
110 all'inizio della linea di divisione, affinché ciò che sarà rimasto sopra il 10, siano i miliari.
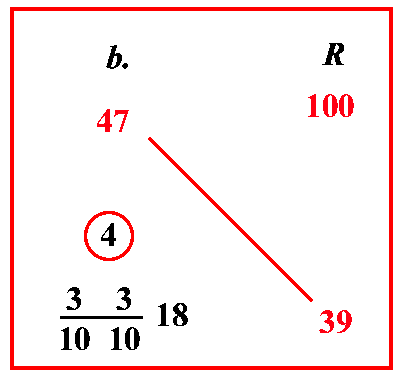
Se un cantaro di una merce qualunque si venda presso i Garbi per 47 bisanti; quanto valgono 39
[NdT]
29 nel testo è un chiaro errore
rotoli: scrivi il problema e moltiplica 47 per 39 che sono di traverso, farà 1833; dividilo per 100, cioè per
10
1010, farà
33
101018 bisanti; cioè
[NdT]
multiplica nel testo ci sembra un errore
18 bisanti e
1103 miliari, e tanto valgono gli altri 39 rotoli.
100 pelli di capra valgono
3442 bisanti; quanto valgono allora 21 pelli di capra: moltiplica 42 per 4 e somma il 3, farà 171; moltiplicalo per 21, farà 3591; dividilo per 100, e per 4, cioè per
100
41010, farà
379
410108 bisanti come costo di quelle 21 pelli di capra.
|
  |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Sul cantaro venduto per bisanti e miliari.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
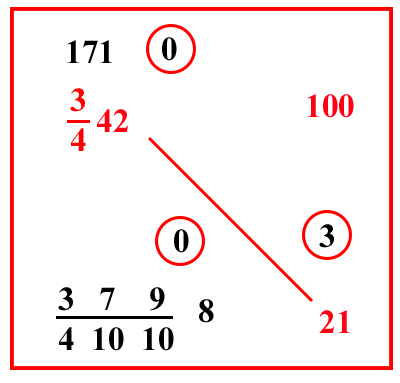
(VIII.1.38 ; G: VIII.97)
Ugualmente un cantaro è venduto per 23 bisanti e
124 miliari
[NdT]
Evidente errore nel testo
; cioè per
14
21023 bisanti, quanto valgono allora
1431 rotoli: moltiplica il 23 per il 10 e somma il 4; e moltiplica per 2 e somma 1, farà 469. Ugualmente moltiplica 31 per 4 e somma 1, farà 125; un quinto di un quinto del quale, cioè 5, moltiplicalo per 469, e dividi il totale per un quinto di un quinto di 100, cioè per 4, e per tutti i numeri che sono sotto la linea di frazione, farà
123
48107 bisanti.
|
 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Decina di panni venduta a Garbo
(PdA)
.
Nessun dubbio che Garbo sia una regione ben precisa, con i suoi porti mercantili, come del resto sanno bene gli storici medievali, che ricordano la migrazione degli ebrei del Garbum alla fine degli anni ’30 del sec. XIII a Palermo e in Sicilia, dove tra l’altro si specializzarono nella tintura. Secondo studi recenti di Giuseppe Mandalà «la cancelleria sveva utilizza il termine Garbum, erede della nozione arabo-islamica di Maġrib/Ġarb (al-aqṣà e al-awsaṭ), per indicare i territori dell’Africa nordoccidentale allora sotto l’influenza politica del califfato almoḥade», a ovest quindi della Barbaría propriamente detta. Probabilmente dalla medesima regione provenivano anche le merci (e le rispettive unità di misura) a cui si riferisce Leonardo. [PdA,pag.6]
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| (VIII.1.39; G: VIII.98) Dieci panni valgono 1434 bisanti, quanto valgono allora 37 panni: moltiplica il 34 per il 4 e somma l’1, farà 137; moltiplicalo per 37, farà 5069; dividilo per il 10, e per il 4 della frazione, cioè per 10 410 farà 17 410126, cioè 126 bisanti e 147 miliari. |
 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Sul rotolo
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
pg.94 |
(VIII.1.40; G: VIII.99)
Un rotolo di zafferano
(PdA)
, o di noci moscate, o di altre merci qualsiasi si vende per 3 bisanti e
147 miliari, cioè per
17
4103 bisanti; quanto valgono allora 17 rotoli e
125 once, cioè
15
21217 rotoli: scrivi il problema come qui si vede, e moltiplica 3 per 10, e somma 7, e per 4 somma 1, farà 149. Ugualmente moltiplica 17 per 12 e somma 5; e per il 2 e somma 1, farà 419; moltiplicalo per 149, e dividi il totale per le frazioni di entrambi i numeri, farà
1320
2681065 come si mostra più sopra nel riquadro
I prodotti importati dall’Oriente prendono la denominazione araba: non solo lo zucchero (succarum > sukkar), che i Romani non conoscevano, ma anche lo zafferano (zaffaranum > za’farān), noto in precedenza come crocus o crocum (dal greco κρόκος — kròkos) [PdA,pag.7]
|
 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Sullo stesso.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
(VIII.1.41; G: VIII.101)
Invero, se nello stesso modo qualcuno chiedesse quanto valgono
125 once; intanto fai le once di 1 rotolo, saranno 12: poi poni nel problema che 12 once di zafferano valgono 3 bisanti e
147 miliari, cioè
17
4103 bisanti; e si chiede quanto valgono
125 once. Moltiplicherai, dunque
(PdA)
, come sopra, il 3 per la sua frazione, farà similmente 149; e moltiplicherai 5 per 2, e sommerai l'1, farà 11; che moltiplicherai per 149, farà 1639; dividilo per 12, e per le restanti frazioni, cioè per
1000
26810, farà
1307
268101 bisanti.
Ora si è detto abbastanza di ciò che attiene ai bisanti miliariensi, nella prima parte di questo capitolo; ora invero si dica di ciò che riguarda i bisanti saraceni o yperperos, per i quali avremo la necessità che si abbia il 24 all'inizio delle frazioni, cioè
10
38: e ciò perché ciascuno di quei bisanti comprende in sé 24 carati
In qualche caso la ridondanza semantica ha prodotto risultati inattesi: siquidem, che ricorre 45 volte nel Liber abbaci, non ha più il valore di congiunzione, ma risulta in tutto sovrapponibile al pur molto usato avverbio quidem: non è un caso che quasi sempre ... sia collocato all’interno della frase. [PdA,pag.3]
(PdA)
; e non dubiterai che siano carati ciò che sarà rimasto sopra
10
38, dalle divisioni.
Anche il Karatus è una unità di moneta e di peso. Il termine ha origine dal greco κεράτιον — keràtion, ma arriva in Occidente per il tramite dell’arabo quirāt. [PdA,pag.5]
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Sul cantaro di lino o qualunque altra merce che si vende in Siria o a Alessandria.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
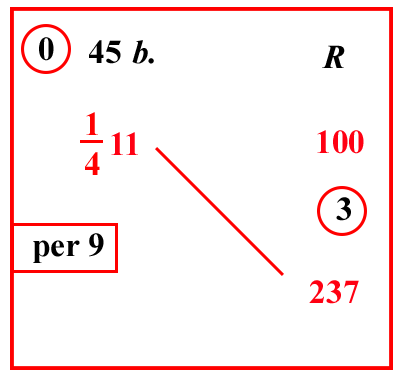
| (VIII.1.42) ; G: VIII.103) Se il cantaro di lino o di qualunque altra merce si vendano in Siria o ad Alessandria per 4 bisanti saraceni, e vorrai sapere quanto valgono 37 rotoli, scrivi il problema, e moltiplica 4 per 37, farà 148; dividilo per 100, farà 84 10101 bisante: se però avrai voluto fare carati di 84 1010 di un bisante, moltiplica il 4 che sta sopra il 10 per l'altro 10, e somma l'8, farà 48; moltiplicalo per i carati di un bisante, cioè per 24, farà 1152; dividilo per 10 1010, farà 25 101011 carati: o perché tu abbia il risultato con una sola moltiplicazione, moltiplica 148 per la quarta parte di 24, cioè per 6, e dividi il totale per la quarta parte di 100, e per la regola di 24, farà similmente 3223 55381 bisante, cioè 1 bisante e 25 101011 carati: perché se avrai moltiplicato il 3 che sta sopra l'8 per il 3 che sta sotto la linea di frazione e sommerai il 2, saranno 11 carati, e 32 55 che sono nella linea di frazione dopo 10 38, sono parti di un solo carato; e così bisogna sempre fare anche in tutti gli altri casi nei quali porrai all'inizio della frazione 10 38, cioè moltiplicare ciò che starà sopra l'8, per il 3 che sarà dopo l'8 nella linea di frazione, e sommare ciò che sarà sopra il 3, come abbiamo fatto ora, e avrai i carati di quella frazione. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Sullo stesso argomento.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| (VIII.1.43 ; G: VIII.106) Ugualmente un cantaro vale 1411 bisanti; quanto valgono quindi 2 cantari e 37 rotoli, cioè 237 rotoli: moltiplica 11 per 4 e somma l'1, farà 45, la cui quinta parte, cioè 9, moltiplicala per 237; moltiplica poi tutto ciò per 3, affinché si abbia la regola del 24 sotto la linea di frazione, farà 6399; dividilo per la quinta parte di 100 e per il 4, che è sotto la linea di frazione, e per il 3, che abbiamo sommato alla moltiplicazione, che verranno sistemati in 100 1038, faranno 905 103826 bisanti, come è esemplificato nel riquadro. |
 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Del milario di olio di Costantinopoli
(PdA)
Di uno statuto a sé stante gode il nome della città di Constantinopolis. Accanto al genitivo Constantinopolis l’unica altra forma tramandata unanimemente dalla tradizione manoscritta è Constantinopolim, che assolve la funzione di accusativo. [PdA,pag.8]
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
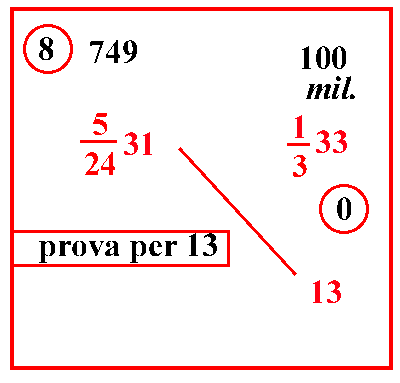
| (VIII.1.44; G: VIII.107) A Costantinopoli, un miliario di olio, che è 1333 metreti, si vende per 52431 bisanti; quanto costano allora 13 metreti: scrivi il problema, e moltiplica 33 per il 3 che sta davanti ad esso, nella frazione, e somma l'1, farà 100; ponilo sopra il 33, come vedi nella figura più in basso: poi moltiplica 31 per 24 e somma il 5, faranno 749 carati; ponili sopra il 31, e moltiplica 749 per 13, farà 9737; moltiplicalo per il 3 che sta sotto la linea di frazione del 33, farà 29211; dividili per il 100, posto sopra il 33 e per 24, cioè per 1000 101038, risulteranno 1111 10103812 bisanti. |
 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Dell’'oncia di Palermo cambiata in moneta pisana
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
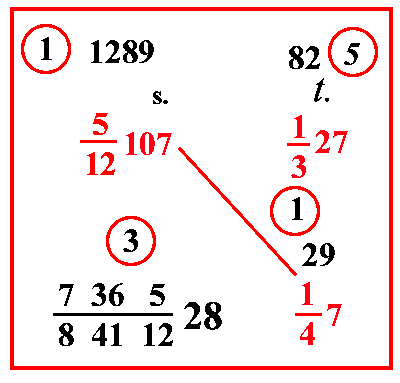
| (VIII.1.45 ; G: VIII.108) Un'oncia di Palermo, che vale 1327 tareni, si cambi lì in moneta pisana da saldare per 512107 soldi. Si chiede quanto valgano, in questo caso, 147 tareni: moltiplica il 27 per il 3 e somma l'1 che è sopra il 3, farà 82, serbalo sopra 27: poi moltiplica 107 per 12, e somma 5, farà 1289 denari, ponili sopra 107. Ugualmente moltiplica 7 per 4 e somma l'1, farà 29; ponilo sopra 147; e moltiplica i numeri che sono di traverso, cioè 1289 per 29, farà 3781; moltiplicalo per il 3 che è sotto l’unica linea di frazione del 27, farà 112143; dividilo per la regola dell'82 e per le frazioni degli altri numeri, cioè per 14, e per 112 che sistemati insieme fanno 100 84112, farà 7365 8411228 soldi. |
 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
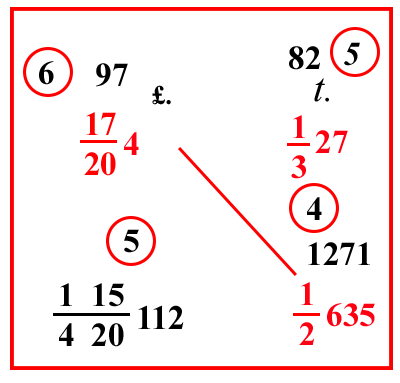
| (VIII.1.46 ; G: VIII.110) Ugualmente la stessa oncia, cioè 1327 tareni, viene prestata per 17204 lire, cioè per 4 lire e 17 soldi, quanto valgono allora 12635 tareni: moltiplica 17204 per 12635, e dividi il loro totale per 1327, che mostriamo come deve essere fatto: cioè, che tu moltiplichi il 27 per il 3 e addizioni l'1, farà 82 , serbalo sopra il 27: poi moltiplica le 4 lire per 20 e somma il 17, farà 97 soldi, ponilo sopra 17204: poi moltiplica 635 per 2 e somma 1, farà 1271, ponilo sopra 12635. E moltiplica 97 per 141 di 1271, cioè per 31, e poi per il 3 che è sotto la linea di frazione davanti al 27, farà 9021; dividilo per 141 di 82, e per 20, e per 2, che sono sotto le linee di frazione, cioè per 10 420; e non occorre moltiplicare per il 3 che manca a 112; perché non restano altre frazioni dopo 14 di 120; e questo quarto appartiene alla scomposizione del 12, farà 115 420112, cioè 112 lire, 15 soldi e 3 denari. |
 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Sui rotoli che si vendono per tareni.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| (VIII.1.47 ; G: VIII.112) 193422 rotoli si vendono per 182514 tareni; quanto valgono 15 2617 rotoli: scrivi il problema, e moltiplica 22 per le sue frazioni, farà 823, ponilo sopra 193422: poi moltiplica il 14 per le sue frazioni, farà 581, ponilo sopra 182514. Ugualmente moltiplica il 17 per le sue frazioni, farà 215 moltiplicalo per 581, farà 124915 che devi moltiplicare per i numeri che sono sotto le linee di frazione del 22, cioè per 4 e per 9, e dividere il totale per 823, e per 5, e per 8, e per 2, e per 6, che sono sotto la linea di frazione dei numeri opposti di traverso, cioè il 14 e il 17. Ma per introdurre la raffinatezza della semplificazione, che abbiamo mostrato nelle moltiplicazioni dei numeri, si tralasci di moltiplicare il 124915 per 4, e per uno dei 3 che stanno nella regola del 9, e poi si tralasci di dividere per 2 e per 6, che sono altrettanto. Ma moltiplicherai il 124915 per il 3 che resta da quel 9, farà 374475, che resta da dividere per 100 58823, cioè per 100 282320, per avere così il 20 sotto l'inizio della linea di frazione, sopra il quale quale risulteranno i grani, farà 15517 28232011 tareni: abbiamo potuto così osservare il detto metodo della semplificazione in alcuni dei sovrascritti commerci. Ma anche quando tralasciamo, affinché non fosse eventualmente impedito quello che abbiamo voluto mostrare, tuttavia in tutte le operazioni simili bisogna osservare questo stesso metodo. | 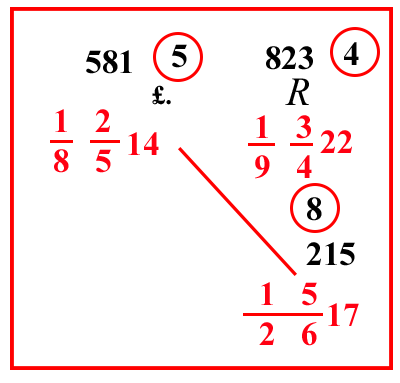 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Sui rotoli e le loro frazioni.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
pg.96 |
(VIII.1.48 ; G: VIII.115) Ugualmente 132 281113 rotoli si vendono per 1514137 bisanti, quanto costa allora 1735 di un rotolo: moltiplica il 13 per la sua frazione, farà 2327 che devi scrivere sopra il 13. Poi moltiplica il 7 per le sue frazioni, farà 467, ponilo sopra il 7, poi moltiplica il 3, che è sopra il 5 per 7, e l'1 che è sopra il 7, per 5, farà 26, ponilo sopra 1735; e moltiplica il tredicesimo di 26 per 467, e per i numeri che sono sotto la linea di frazione del 13, cioè per 2, e per 8, e per 11, farà 164384; dividilo per i tredicesimi di 2327, cioè per 179, e per i numeri che sono sotto le linee di frazione dei numeri che sono di traverso: tuttavia poiché da loro non possiamo ricavare la regola di 24; perché da essi possiamo avere solo 1413, e ci manca 12, si sommi il 2 nella divisione, e si moltiplichi 164384 per 2, farà 328768; dividilo per 100000 55717938, farà 3348813 55717938. | 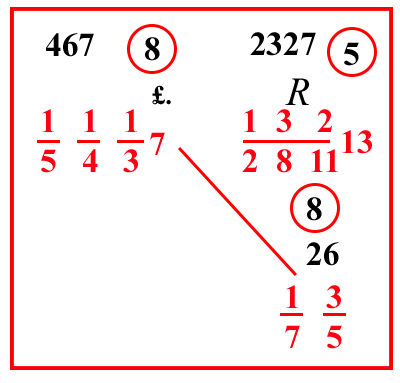 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Su una parte di rotolo per una parte di bisanti.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
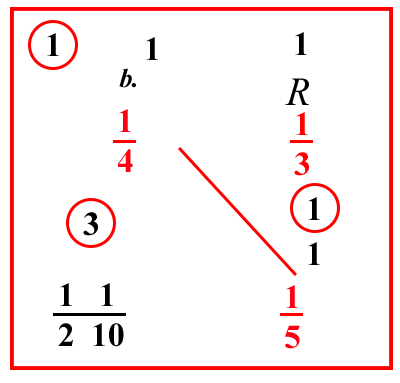
| (VIII.1.49 ; G: VIII.118) Ugualmente 13 di un rotolo è dato per 14 di un bisante; quanto vale allora di 15 di un rotolo: scrivi il problema, e moltiplica i numeri che sono di traverso, cioè 14 per 15 e dividi per 13, questo si fa così: moltiplica l'1 che è sopra il 4, per l'1 che è sopra il 5, farà 1; moltiplicalo per 3, farà 3: dividilo per l'1 che è sopra il 3, e per il 4, e per il 5 che sono sotto le linee di frazione, cioè per 10 210, farà 11 210 di un bisante, cioè 320: se da questi, avrai voluto fare dei carati, moltiplica il 3 che sta sopra il 20 per la quarta parte di 24, farà 353 carati. |
 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Su una parte di rotolo per una parte di soldo.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
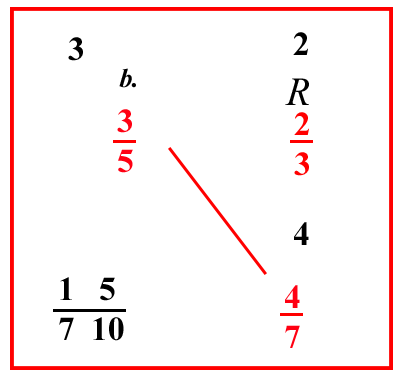
| (VIII.1.50; G: VIII.119) Ugualmente 23 di un rotolo per 35 di un soldo; quanto vale quindi 47 di un rotolo: moltiplica il 3, che è sopra il 5. per il 4, che è sopra il 7, e per 3, che è sotto la linea di frazione, farà 36; dividilo per il 2 che sta sopra il 3, e per il 5, e per il 7, cioè per 10 710, farà 15 710 di un soldo, cioè 11 576 denari |
 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Sulle parti di rotolo per parti di bisante.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| (VIII.1.51; G: VIII.120) Ugualmente 1423 di un rotolo per 1615 di un bisante; quanto vale quindi 15 29 di un rotolo: moltiplica 1615 per 15 29 e dividi per 1423, che si fa così: moltiplica il 2, che è sopra il 3, per 4; e l'1 che è sopra il 4 per 3 e sommali insieme, farà 11, ponilo sopra 1423. Ugualmente moltiplica l'1 che sta sopra il 5, per 6, e l'1 che sta sopra il 6, per il 5, e sommali insieme, farà 11, ponilo sopra 1615. Ugualmente moltiplica il 5 che sta sopra il 9 per 6, e somma l'1, farà 11; ponilo sopra 15 29, e moltiplica l'11 che sta sopra 1615 per l'11 che sta sopra 15 29, e per 3, e per 4, che sono sotto le linee di frazione e dividi il totale per l'11 che sta sopra 1423 e per gli altri rotti [ denominatori ]. Ma poiché devi moltiplicare per 11, e per 3, e per 4, e dividere per 11, e per 2, e per 6, tralascia di moltiplicare per l'11 che sta sopra 1615; né per 3, né per 4, che sono sotto le linee di 1423, e non dividere per 11, nè per 6; ma dividi l'11, che è sopra 15 29, per 10 59, che è sotto le linee di frazione, farà 12 59. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
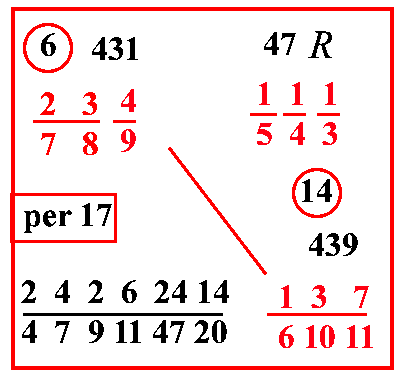
| pg.97 | (VIII.1.52 ; G: VIII.123) Ugualmente 151413 di un rotolo per 23 7849 di un tareno; quanto vale 137 61011 di un rotolo: moltiplica l'1 che è sopra il 3, per 4, e per il 5, farà 20; e moltiplica l'1 che sta sopra il 4 per il 5; e per 3, farà 15; e moltiplica l'1 che è sopra il 5 per 4; e per 3, farà 12; e somma il 20 con il 15, e con il 12, farà 47, ponilo sopra 151413: poi moltiplica il 4 che è sopra il 9, per 8, e per 7, farà 224; e moltiplica il 3 che sta sopra l'8, per 7 e somma il 2, farà 23; e per 9, farà 207; sommalo con 224, farà 431, ponilo sopra 23 7849. Ugualmente moltiplica il 7 che sta sopra l'11, per 10 e somma 3; e per 6, e somma 1, farà 439; scrivilo sopra 137 61011, e moltiplica 431 per 439 che sono di traverso, farà 189209, che dovresti moltiplicare per i rotti [ i denominatori ] che sono sotto il 47, cioè per 3, e per 4, e per 5, e dividere per lo stesso 47, e per i rotti, che sono sotto le altre frazioni: ma si tralasci la moltiplicazione di 3 e di 2, che sono nella regola del 241 ; e si moltiplichi il 189209 solo per il 2 che resta dal 4, e per il 5, cioè per 10, farà 1892090; e si tralasci di dividere per il 6, che sta sotto la linea di frazione di 100 61011, perciò si divide per 100000 789101147, cioè per avere 120 in cima alla linea di frazione per 100000 479114720, saranno 24262414 479114720 grani. |
 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| (VIII.1.53 ; G: VIII.126) Ugualmente 100 libbre di pepe sono vendute per un qualche costo, poniamo per 1411 lire; e si chiede quanto vale 1 rotolo: poiché le 100 libbre e 1 rotolo sono dello stesso genere, ma non sono della stessa quantità perché le libbre sono 100 e il rotolo è 1, devono essere ridotti: e poiché sono dello stesso genere siano di una sola quantità, o della quantità dei rotoli o della quantità delle libbre: ed essendo dell'uno e dell'altro tipo, mostriamo come farne di lì qualcosa d'altro, cioè che si riconducano entrambi a parti di cantaro, in modo cioè che tu veda che parti siano di un cantaro le 100 libbre: infatti ogni libbra pisana è 1158 di cantaro, perciò 100 libbre sono 100158 di un cantaro, e 1 rotolo è 1100 dello stesso cantaro; perciò così ridotti in questo problema, si ricava che 100158 di un cantaro valgono 1411 lire; e si chiede quanto valga 1100 di un cantaro: scrivi allora il problema in questo modo e avrai operato secondo ciò che abbiamo mostrato più sopra, e avrai per il costo di quel rotolo 06663 1010101220. | 1 cantaro = 100 rotoli
=158 libbre pisane 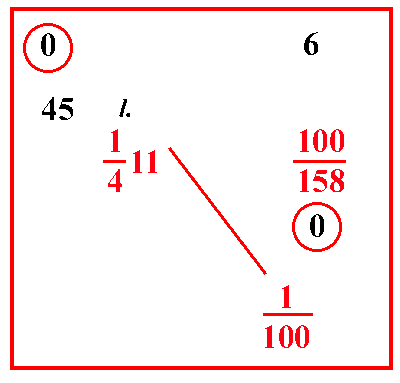 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| (VIII.1.54; G: VIII.128) Ugualmente 128 libbre per 3241211 soldi; quanto vengono 13289 rotoli: delle 128 libbre fai parti di un cantaro, farà 182158; e dei 13289 rotoli fai similmente parti di cantaro, e farà 13928100; scrivi il problema, e moltiplica l'8 che è sopra il 158 per 2 e somma l'1, farà 17; che ponilo sopra 182158, e moltiplica l'11 per il 12 e somma 2; e per 4, e somma il 3, farà 539, ponilo sopra il 3241211: poi moltiplica il 9 che sta sopra il 100 per 8 e somma il 3; e per 2 e somma l'1, farà 151; ponilo sopra il 13928100, e moltiplica 151 per 539, farà 81389, che dovresti moltiplicare per 2, e per 158, che sono sotto la linea della frazione sotto il 17, e dividere per lo stesso 17, e per i rotti delle altre frazioni. Ma tralascerai la moltiplicazione del 2, che è davanti al 158 nella frazione, e la moltiplicazione del 2 che è nel 158, ma moltiplica solo 81389 per la metà di 158, cioè per 79, e per quei due 2, per i quali non hai moltiplicato, tralascia di dividere per il 4 che è nella linea di frazione davanti 12: infatti la moltiplicazione di 81389 per 79 dà 6429731, che diviso per 100000 2810101712, farà 118568 281010171219 soldi. | 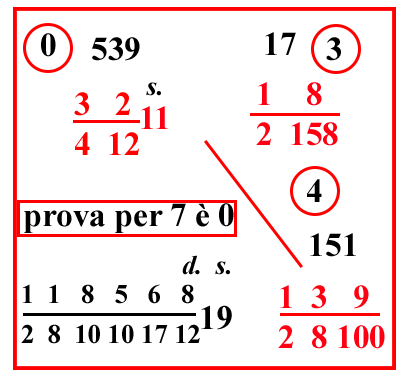 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| (VIII.1.55 ; G: VIII.131) Ugualmente 193511 rotoli, cioè 1311 95100 di cantaro, si vendono per 1321019 denari; quanto valgono 11019347 libbre, cioè 1137 1094158 di cantaro: scrivi il problema, e moltiplica l'11 che è sopra il 100, per 5, e somma il 3, e moltiplica per 9 e somma la moltiplicazione di1, che è sopra il 9, per 5, farà 527, ponilo sopra 1311 95100 . Ugualmente moltiplica 19 per 10 e somma 3; e moltiplica per 2, e somma l'1, farà 387, ponilo sopra il 1321019: e poi moltiplica il 7, che è sopra il 158, per 4, farà 2866, e moltiplica 387 per 2866, farà 1109142: e dovendolo moltiplicare per 5, e per 9, e per 100 che sono sotto il 257, sotto la linea di frazione, e [ dovendo ] dividere il totale per la regola di 527, che è 101731, e per gli altri numeri che sono sotto la linea di frazione dei due numeri restanti, non si moltiplichi per 9, né per 100; e non si divida per il 9, né per il 10 che sono nella frazione sotto il 2866: né per il 10 che è sotto la linea di frazione sotto il 387: quindi moltiplicherai l'1109142 solo per 5, farà 5545710; dividilo per 1000 24158527 , cioè per 10000 28173179 , farà 07102125 28173179 8 denari. | 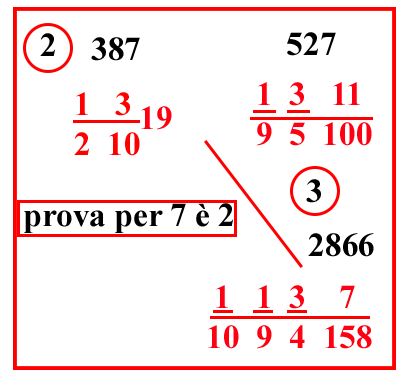 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
pg.98 |
(VIII.1.56 ; G: VIII.135)
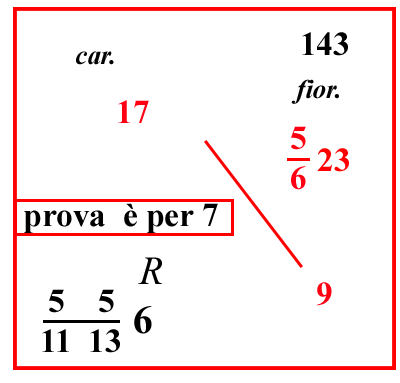
Parimenti 11 rotoli gerovini
(PdA)
valgono ad Alessandria 17 carati: quanto valgono 9 rotoli forforini: poiché gli 11 rotoli e i 9 rotoli non sono dello stesso peso, o fai degli 11 rotoli gerovini dei rotoli forforini o dei 9 rotoli forforini fai dei rotoli gerovini, in modo che siano entrambi o forforini o gerovini; ma poiché puoi trasformare più facilmente gli 11 rotoli gerovini in rotoli forforini che trasformare i 9 rotoli forforini in rotoli gerovini, dal momento che ciascun rotolo gerovino equivale a
162 rotoli forforini, così se moltiplicherai gli 11 rotoli gerovini per
162 ne farai
5623 rotoli forforini. Perciò scrivi che
5623 rotoli forforini valgono 17 carati; quanto valgono 9 rotoli forforini? Moltiplicherai dunque il 17 per il 9, che sono in diagonale. e dividerai per
5623, faranno
5511136 carati
In Egitto l’unità di peso delle spezie era il fulfulī, una varietà del raṭl (lat. rotulus), la centesima parte del ḳinṭār (da cui lo sp. quintal e l’it. quintale, ma anche il lat. cantare o cantar(i)um o cantarus e l’it. cantàro; cf. gr. κεντηνάριον — kentenàrion). Assai diffuso era anche il djarwī, un tipo di raṭl utilizzato in origine per pesare l’olio. In genere 1 ḳinṭār fulfulī equivale a 144 libre (quasi kg. 4,5), 1 ḳinṭār djarwī a 312 libre (oltre kg. 9,5). Prendendo in prestito i due termini arabi Leonardo e gli autori successivi parlano di rotuli (o di cantaria) forfori e gerovi (o geroui), oppure aggiungono ai due sostantivi indeclinabili il suffisso latino -nus, -a, -um, coniando gli aggettivi forforinus e gerovinus [PdA,pag.5]
|
 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Sui rotoli forforini
(PdA)
quando si chiede il costo e viceversa.
In Egitto l’unità di peso delle spezie era il fulfulī, una varietà del raṭl (lat. rotulus), la centesima parte del ḳinṭār (da cui lo sp. quintal e l’it. quintale, ma anche il lat. cantare o cantar(i)um o cantarus e l’it. cantàro; cf. gr. κεντηνάριον — kentenàrion). Assai diffuso era anche il djarwī, un tipo di raṭl utilizzato in origine per pesare l’olio. In genere 1 ḳinṭār fulfulī equivale a 144 libre (quasi kg. 4,5), 1 ḳinṭār djarwī a 312 libre (oltre kg. 9,5). Prendendo in prestito i due termini arabi Leonardo e gli autori successivi parlano di rotuli (o di cantaria) forfori e gerovi (o geroui), oppure aggiungono ai due sostantivi indeclinabili il suffisso latino -nus, -a, -um, coniando gli aggettivi forforinus e gerovinus [PdA,pag.5]
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
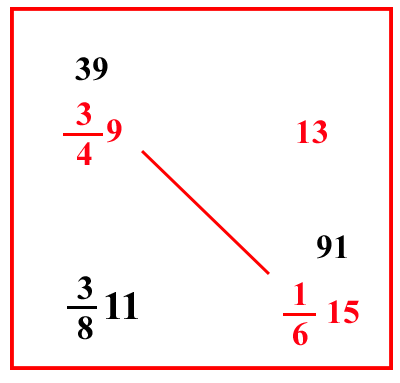
| (VIII.1.57 ; G: VIII.137) Ugualmente 13 rotoli forforini valgono 349 carati; quanto valgono 7 rotoli gerovini: fai dei rotoli forforini con i 7 rotoli gerovini, cioè: moltiplicherai i 7 rotoli gerovini per 162, farà 1615 rotoli forforini: quindi scriverai che 13 rotoli forforini valgono 349 carati, quanto valgono 1615 rotoli forforini: moltiplicherai 349 per 1615, e dividerai per 13, e semplificherai di lì 113, perché si può fare, e similmente , faranno 3811 carati. |
 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
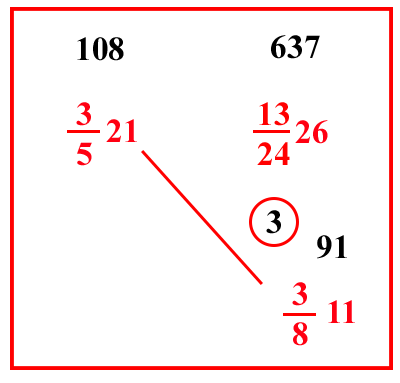
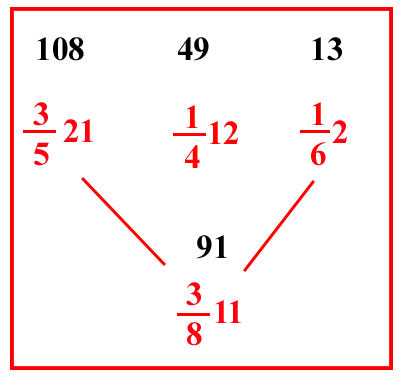
| (VIII.1.58 ; G: VIII.138) Ugualmente 1412 rotoli gerovini sono venduti per 3521 carati, quanto valgono 3811 rotoli forforini: fai rotoli forforini dai 1412 rotoli gerovini, cioè moltiplica 1412 per 162, farà 132426 rotoli forforini: poi scrivi che 132426 rotoli forforini valgono 3521 carati, quanto valgono 3811 rotoli forforini: moltiplicherai 3521 per 3811, e dividerai per 132426, faranno 00333 47710139 carati, come si vede in questo riquadro: possiamo infatti operare ugualmente evitando la moltiplicazione di 1412 per 162, che più sopra abbiamo moltiplicato, cioè se si scrivono nel riquadro del problema i 3811 rotoli forforini sotto a 1412 rotoli gerovini: poi guarda a quanti rotoli forforini corrisponda un rotolo gerovino, cioè 162: poni invero 162 prima di 1412, come si vede in figura; e allora la domanda sarà : se 162 [ di ] 1412 rotoli forforini valgono 3521 carati, quanto valgono allora 3811 rotoli forforini: moltiplicherai dunque, come abbiamo detto precedentemente, i 3521 per 3811, e dividerai per 1412 e per 162, e questo si fa così: cioè moltiplica 2 per 6 e somma l'1 che è sopra il 6, farà 13; ponilo sopra 162, e moltiplica il 12 per 4 e somma l'1, che è sopra il 4, farà 49, ponilo sopra 1412. Ugualmente moltiplica 21 per 5 e somma il 3, farà 108, ponilo sopra 3521; e poi moltiplica l'11 per l'8 e somma il 3, farà 91, ponilo sopra 3811, e moltiplica 108 per 91, e per i rotti che sono sotto il 49 e sotto il 13, cioè per 4 e per 6, farà 235872; dividilo per 13, e per 49, e per i numeri che sono sotto le linee di frazione degli altri due numeri, cioè per 5 e per 8, cioè per 10000 4771013, farà 00333 47710139 carati, come troviamo più sopra. |
  |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
(VIII.1.59; G: VIII.142)
Oppure scrivi il problema in un altro modo, cioè i
3811 rotoli forforini sotto
1412 rotoli gerovini, e vedi quante parti sia 1 rotolo forforino di un rotolo gerovino, cioè
613 per questo motivo: poiché 1 rotolo gerovino è 2
162 rotoli forforini, allora 6 rotoli gerovini sono 13 rotoli forforini. Quindi 1 rotolo forforino è
613 di rotolo gerovino, come abbiamo detto precedentemente: poni dunque i
613 dei
3811 rotoli forforini, come più sopra, nel precedente esempio, abbiamo posto
162
[NdT]
Abbiamo aggiunto il 2 per coerenza
davanti a
1412 rotoli gerovini, come si vede in questa descrizione: e la domanda sarà dunque questa:
1412 rotoli gerovini valgono
3521 carati, e si chiede quanto valgano
613 di
3811 rotoli gerovini; questo lo farai così: moltiplicherai
3521 per
3811613 e dividerai per
1412 così: moltiplica 12 per 4 e somma l'1, farà 49, ponilo sopra 1412, e per lo stesso motivo poni il 108 sopra i
3521 e il 91 sopra i
3811; e moltiplica il 108 per i numeri che sono di traverso, cioè per il 91 e per il 6 e per il 4, che sono sotto il 49, farà similmente 235872 dividilo per la regola di 49 e per i rotti che sono sotto le linee di frazione dei restanti numeri, cioè per
100
5813, che sistemati con la regola del suddetto 49 fanno similmente
10000
4771013, per il quale avrai diviso il 235872, farà
00333
47710139 carati, lo stesso risultato che abbiamo raggiunto prima:
|
 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
pg.99 |
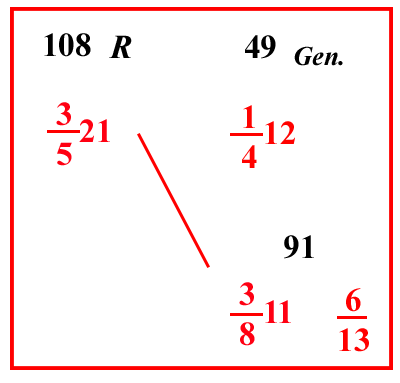
(VIII.1.60; G: VIII.146) e affinché non fosse ostacolato ciò che volevamo dimostrare in questo riquadro , non abbiamo evitato la fatica del moltiplicare e del dividere, che avremmo potuto semplificare. Ma affinché non si smetta di insegnare di semplificare il lavoro, quando possibile, mostriamo come si debba semplificare in questa situazione: e cioè che non dobbiamo mai moltiplicare un numero qualunque per un altro quando il totale della loro moltiplicazione si debba poi dividerlo per uno o più numeri simili, come quando moltiplicammo 108 per 91, e per 6, e per 4, che sono sotto la linea di frazione del 49; e abbiamo diviso il totale per 10000 4771013: avremmo potuto dunque tralasciare, in questa moltiplicazione, di moltiplicare per il 91 e per alcuna parte di esso, poi avremmo potuto tralasciare la divisione per il 7 e per il 13 che sono nella linea della divisione, e che equivalgono a 91, perché 7 per 13 fa 91, e poiché si equivalgono allora sono simili: e questo è ciò che diciamo, che non dobbiamo moltiplicare 91 nella detta moltiplicazione dovendo poi dividere per 10 710: resta dunque da moltiplicare 108 per 6, e per 4, e si divida solo per 100 4710, da cui possiamo ancora semplificare, cosicché non moltiplichiamo il prodotto di 6 per 108 per 4 e non lo dividiamo per il 4 che sta nella linea della divisione. Moltiplicheremo, dunque soltanto il 6 per la metà di 108, farà 324; dividilo solo per 10 57, farà 41 579 carati che sono tanti quanto 00333 47710139. |
Semplifica le frazioni
 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| (VIII.1.61; G: VIII.149) E che questo risultato sia vero, si sappia così: moltiplica il 3 che sta sopra il 13 per il 10 che sta davanti al 13 sulla linea di frazione e somma il 3 che sta sopra il 10, farà 33; moltiplicalo per il 7 e somma il 3 che sta sopra il 7, farà 234, dividilo per 100 13107, farà 41 57: infatti è più bello dire 41 57 che 333 71013: perciò bisogna sempre impegnarsi a semplificare ciò che può essere semplificato, affinché il lavoro sia minore e si abbiano delle frazioni più belle e più comprensibili. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Sui rotoli forforini quando si richiedono dai gerovini.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| (VIII.1.62 ; G: VIII.150) Ugualmente 151413 rotoli forforini per 17569 carati: quanto valgono quindi 19387 rotoli gerovini: scrivi il problema come se che i rotoli fossero dello stesso peso; poi poni 613 prima [ a destra ] dei rotoli forforini, oppure prima dei rotoli gerovini poni 162 per lo stesso motivo, che abbiamo mostrato più sopra: in questo riquadro poniamo dunque i 613 prima dei 151413 rotoli forforini, come qui si mostra; e moltiplicherai il 13 per le sue frazioni, farà 269; poi moltiplicherai il 9 per le sue, farà 419. Ugualmente moltiplica il 7 per le sue frazioni, farà 539; poi moltiplica 419 per 539 che sono di traverso; moltiplicalo per i rotti del numero restante, cioè per 4 e per 5 e per 13 e dividi il totale che ne uscirà per il 6, che sta sopra il 13, e per il 269, e per i rotti dei rimanenti due numeri, cioè per 6 e per 7 e per 8 e per 9; e semplificherai ciò che puoi semplificare, come abbiamo mostrato nel problema precedente e avrai 07228 789926912 carati: e così puoi fare in qualsiasi situazione simile, nella quale si proponga la vendita di rotoli di un certo peso, e tu abbia richiesto il costo dei rotoli di qualsiasi altro peso. |
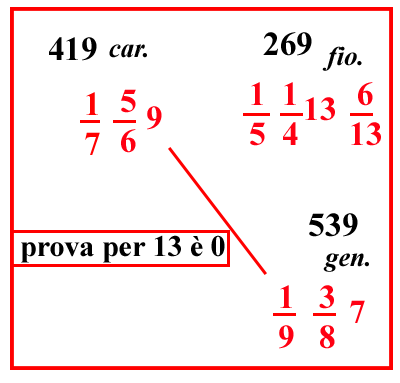 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
pg.100 |
(VIII.1.63 ; G: VIII.152) Ugualmente affinché si comprenda meglio, 14 2714 rotoli di Messina valgono 1925 tareni, e si chiede quanto valgano 173417 rotoli di Pisa. Dapprima bisogna cercare quanti rotoli pisani pesi un rotolo di Messina, cioè 142, così li poniamo in questo modo: ponili davanti ai rotoli di Messina, come più sopra abbiamo insegnato a porre 162 davanti ai rotoli gerovini, o poni 49 prima dei rotoli pisani poiché un rotolo pisano è 49 di rotolo di Messina. Ma qui poniamo 142 davanti ai rotoli di Messina, come qui si mostra; e moltiplica il 2 per 4 e somma l'1, farà 9, ponilo sopra 142: poi moltiplica 14 per la sua frazione, farà 205, ponilo sopra il 14. Ugualmente moltiplica il 7 per le sue, farà 338, ponilo sopra il 7. Ugualmente moltiplica 17 per i suoi rotti, farà 501; ponili sopra il 17, e moltiplica 338 per 501; e per i rotti che sono sopra, cioè per 2, e per 7, e per 4; e dividi per 9 e per la regola di 205 e per i rotti rimanenti, cioè per 1000 4579, e semplificherai ciò che potrai semplificare. E come costo di quei rotoli avrai 228231 35941204 tareni. Terminate quindi le spiegazioni sulle vendite delle merci, nelle quali si trovano i prezzi delle merci, ora invero ritorniamo a quelle stesse vendite, nelle quali si ricerchino le merci dei prezzi posti, in base alla diversità di quelle vendite, tornando dunque alla vendita dei cantari. |
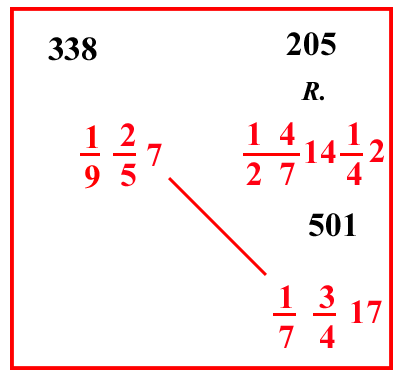 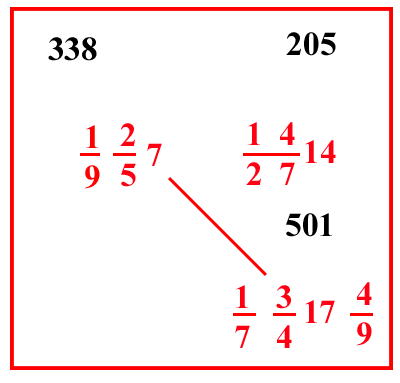 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Sul cantaro quando si vende per le lire; e si chiedono rotoli dalle lire.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| (VIII.1.64; G: VIII.156) Se un cantaro di una merce qualunque si vende per 13 lire; e si chieda quanti rotoli uno potrebbe ottenere per 5 lire, scrivi, come abbiamo detto riguardo alle precedenti posizioni nella prima vendita, i 100 rotoli, poi di seguito sulla stessa riga poni il costo di quei rotoli, cioè 13 lire, poi poni le 5 lire sotto il 13: perché sono dello stesso genere e della stessa quantità, cioè del costo; e scritti i numeri, come qui si mostra, moltiplicherai i numeri che sono di traverso, cioè 5 per 100, farà 500; dividilo per 13, farà 61338 rotoli, come si vede in questo riquadro; e avrai avuto tanti rotoli per le 5 lire scritte: per esempio se vorrai fare delle once da 613 di un rotolo, moltiplica il 6 che sta sopra il 13, per il 12, perché un solo rotolo pesa 12 once, farà 72 ; dividilo per 13, farà 7135 once; di questi 713 di un’oncia possiamo fare nello stesso modo delle parti di un’oncia, secondo che parti siano state dell'oncia stessa, o di rotolo pisano, o di libbra, o di qualche altro rotolo: e affinché si comprenda meglio, poniamo che questi 713 siano di oncia di libbra pisana: per cui se vorremo sapere quanti denari di cantaro si ricavino da essi; poiché un'oncia della stessa libbra pesa 25 denari di cantaro, moltiplicherai il 7, che sta sopra il 13 per il 25, e dividerai per 13; e così intendi per qualunque oncia. |
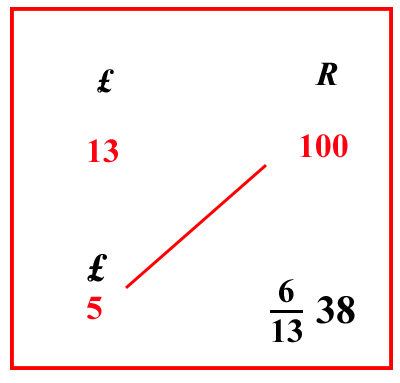 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Sullo stesso argomento con i rotti.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| (VIII.1.65 ; G: VIII.159) Ugualmente un cantaro vale 1416 lire e si chiede quanti rotoli qualcuno avrà avuto per 78 12203 lire: scrivi il problema in questo modo, e moltiplica 16 per 4, e somma l'1, farà 65, ponilo sopra 1416 libbre: poi moltiplica 3 per la sua linea di frazione, farà 823; ponilo sopra il 78 12203, e moltiplica 100 per 823; e per il 4 che sta sotto la linea di frazione del 16, e dividi il totale per la regola del 65 che è 10 513 e per i fratti della frazione più in basso, cioè per 10 1220, e sistemerai il 12 all'inizio della frazione; poiché che quelle che saranno state sopra il 12 sarà l'oncia o le once; dunque la sistemazione di quei numeri sarà 1000 5132012: ma per evitare il lavoro di moltiplicare e dividere, si abbandoni la moltiplicazione del 100 e si abbandonerà la divisione di 10 520 che sono sulla linea della divisione: quindi moltiplicherai 823 per 4, e dividerai solo per 10 1312, farà 31 131221 rotoli: la verifica inoltre di questa faccenda e di casi simili è la stessa che abbiamo mostrato più sopra, cioè: come sarai andato avanti con i numeri, moltiplicando e dividendo, così andrai avanti usando una prova qualunque. Per questo troverai che la prova del 7 di questo argomento è 2. |
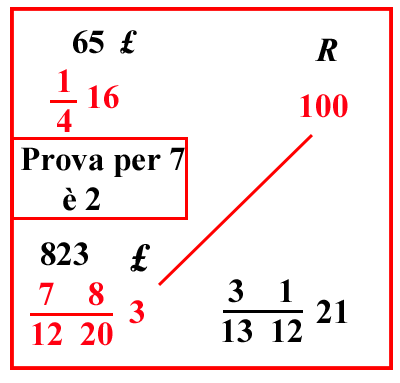 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Sul centone di pepe secondo il modo scritto sopra.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
pg.101 |
(VIII.1.66 ; G: VIII.161)
Ugualmente un centone di pepe è venduto per 12 lire, e 7 soldi, e 5 denari, cioè per
57
122012 lire, quante libbre di pepe avrò avuto per 11 soldi, e 9 denari: poiché le
57
122012 lire e i
9
1111 soldi sono di un unico genere, cioè quello del costo, ma non sono della stessa misura; perché il 12 sono lire e l’11 sono soldi: perciò o delle
57
122012 lire bisogna farne soldi, oppure dei
9
1111 soldi bisogna farne lire, cioè parti di una lira; in modo che come sono di uno stesso genere, così siano anche di una stessa misura: quindi dai
9
1111 soldi facciamo le parti di una lira, che sono
911
1220, e li si scriva sotto le
57
122012 libbre, come si mostra in questo riquadro; e si moltiplichi il 12 per la sua frazione, farà 2969
[NdT]
269 nel testo è un chiaro errore
. Ugualmente moltiplica l'11 per il 12 e somma il 9, farà 141; e moltiplica 141 per 100; e per 12 e per 20 che sono sotto la linea di frazione del 12, e dividi il totale per 2969 e per
10
1220: ma perché tu eviti del lavoro, non moltiplicare per 12 né per 20; e non sarà necessario dividere per
10
1220: quindi moltiplicherai 141 per 100, farà 14100 che dividerai per 2969, oppure, per avere le once sopra la linea di frazione, moltiplica 14100 per 12 e dividi per
10
296912, farà
29368
2969124 rotoli.
|
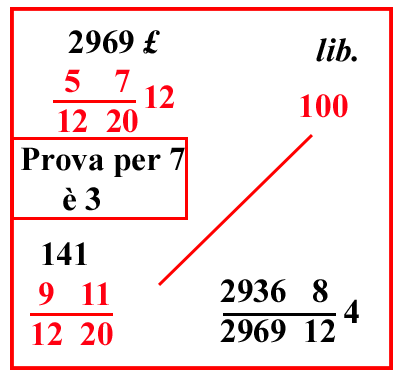 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Sul cantaro venduto per libbre quando si chiedono le merci vendute per denari.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| (VIII.1.67 ; G: VIII.163) Ugualmente un cantaro vale 1 92 513 lire e si chiede quanto uno avrà avuto per 1 49 denari, cioè per 190 41220 di una lira, perché siano della stessa quantità di 1 92 513 lire: si scriva il problema come qui si mostra; e moltiplica il 13 per le sue frazioni, farà 608. Ugualmente moltiplica il 9, che sta sopra il 12, per il 4 e somma l'1, farà 37; e moltiplica il 37 per 100; e per 5, e per 9 che stanno sotto le linee di frazione davanti al 13; e dividerai il totale per la regola di 608, che è 100 4819, e per 100 41220; questi rotti, sistemati insieme, fanno 100000 488101912; e avrai la quantità richiesta: o se avrai voluto semplificare, non moltiplicare il 37 per tutto il 100, ma togli 10 dalla regola del 100, perciò togli 1 10, che è nella linea della divisione: dunque moltiplicherai 37 per il 10 che resta da 100, e per il 5, e il 9 detti prima, farà 16650; dividili per 10000 4881912, farà 22083 4881912. |
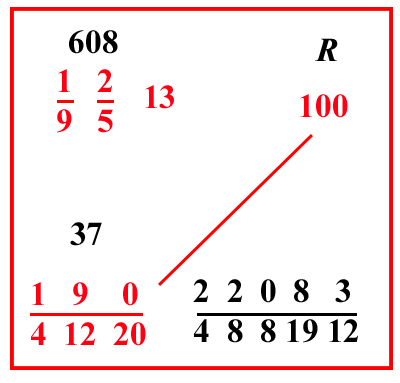 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| (VIII.1.68 ; G: VIII.166) Ugualmente se un centenario si venda per 1 82 317 soldi; e si chieda quanto qualcuno avrà avuto dalla stessa merce per 1 73 417 lire, converti i 1 82 317 soldi in parti di una libbra, farà 1217 8320 di una libbra, e farai ciò affinché entrambi i numeri siano dello stesso nome: poi scriverai il problema in questo modo; e avrai operato secondo ciò che è stato detto più sopra, e avrai, per la quantità richiesta di quella merce 53304 7761122011. |
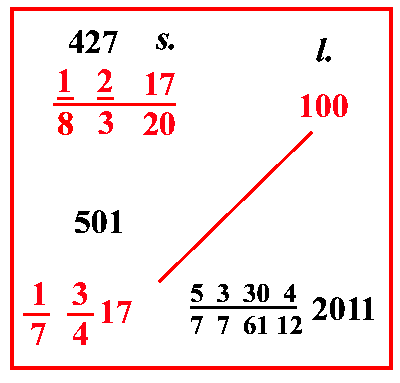 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Regola universale per il centenario.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| (VIII.1.69; G: VIII.167) Vogliamo dunque mostrare una certa regola, che si crea dalla semplificazione delle moltiplicazioni e delle divisioni degli stessi numeri, che sono posti in simili questioni; e cioè, quando si pone che un centenario di pepe valga quante si vogliano lire senza frazioni, per esempio poniamo 13 lire; e si richieda quanto pepe uno avrà avuto per quanti si vogliano denari, per esempio 3; moltiplica sempre i denari per 5 e dividili per il costo del centenario, in questo modo: moltiplica i 3 denari per 5, farà 15: dividilo per 13, farà 2 131; e tante once avrai per i 7 denari: invece se per la stessa ragione si chieda quanto egli avrebbe per 7 soldi, moltiplicherai similmente il 7 per il 5, farà 35 che devi dividere similmente per il 13, risulteranno 9 132 libbre. e così devi intendere in tutti i problemi simili. Ugualmente se viceversa avrai chiesto, per la stessa ragione, quanto valgano 7 once, moltiplicherai 7 per 13 e dividerai per 5, farà 1 518 denari. Infatti se avrai chiesto quanto valgano 7 libbre della stessa merce; moltiplicherai similmente 7 per 13 e dividi per 5, farà 1 518 soldi, cioè 18 soldi e 2 52 denari. E così farai in casi simili. |
1 lira=12×20 denari
1 centenario=100×12 once |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
pg.101 |
(VIII.1.70; G: VIII.170) Ugualmente 14 rotoli per 5 65 tareni; quanti rotoli avrò avuto dagli stessi per 2 517 tareni: Scrivi il problema in questo modo; e moltiplica i numeri che sono di traverso, cioè 14 per 2 517, e dividi per 5 65, farà 309 551241. |
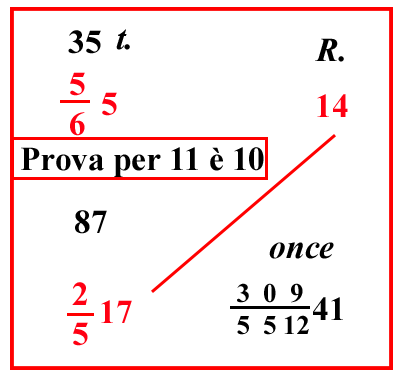 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| (VIII.1.71; G: VIII.171) Ugualmente 1 217 rotoli sono venduti per 1 311 tareni; quanto avrò avuto degli stessi rotoli per 1 47 grani, cioè per 17 420 di un tareno in modo che siano fatti dalla quantità degli 1 311 tareni scritti precedentemente: scrivi così il problema; e moltiplicherai 1 217 per 17 420, e dividi per 1 311, e fai in modo di avere 12 all'inizio della linea di frazione per le once, e faranno 71126 8101712 once. |
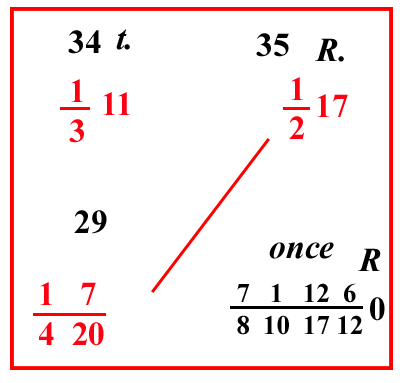 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Sui rotoli venduti per grani quando si chiedono merci per tareni.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| (VIII.1.72 ; G: VIII.172) Ugualmente 1 41 33 rotoli sono venduti per 1 62 513 grani; quanti rotoli avrò avuti per 1 82 711 tareni: fai parti di un tareno da 1 62 513 grani, farà 1213 6520; e scrivi il problema come si vede più in basso e moltiplicherai 1 41 33 per 1 82 711 e dividerai per 1213 6520, farà 33123 711371260 rotoli. |
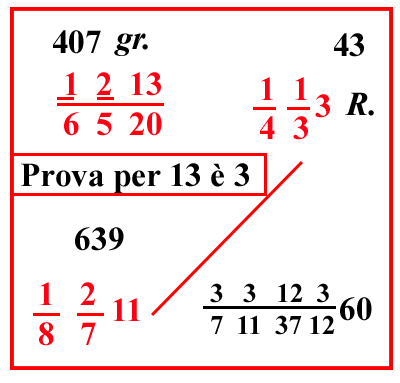 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| (VIII.1.73 ; G: VIII.173) Ugualmente 3 4 di un rotolo è venduto per 4 5 di un bisante, quanto avrò avuto per 6 7 di un bisante: scrivi il problema, e moltiplica il 3 che è sopra il 4 per 6 che è sopra il 7, farà 18; e per 5, che sta sotto la linea di frazione superiore, farà 90; dividilo per il 4 che è sopra il 5, e per 4, e per 7, che sono sotto le altre linee di frazione, cioè per 100 278, farà di 36 78 di un rotolo. |
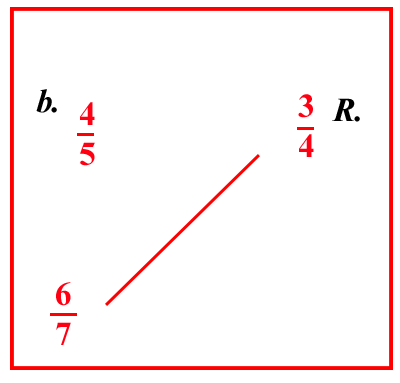 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Sui rotti di rotoli.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| (VIII.1.74; G: VIII.174) Ugualmente 1 42 3 di un rotolo è venduto per 1 71 62 5 di un bisante; quanto avrò avuto in rotoli per 147 8910 di un bisante: scrivi così il problema così e moltiplica 1 42 3 per 147 8910, e dividi per 1 71 62 5, che si fa così: prendi prima il 1 42 3, e moltiplicherai il 2 che è sopra il 3, per il 4, e l'1 che è sopra il 4 per il 3, e sommali insieme, farà 11; ponilo sopra 1 42 3, e troverai il numero di 1 71 62 5, farà 149; ponilo sopra 1 71 62 5, e troverai il numero di 147 8910, farà 537: e moltiplicherai l'11 per 537, il cui prodotto moltiplicherai per i fratti che sono sotto le linee di frazione sotto il 149, cioè per 5 e per 6 e per 7; e dividerai il totale per 149 e per i fratti che sono sotto l'11 e sotto il 537, cioè per 10000 348910, che sistemati insieme sono 10000 891014912: semplificherai ciò che potrai semplificare, farà 388311 41014912. | 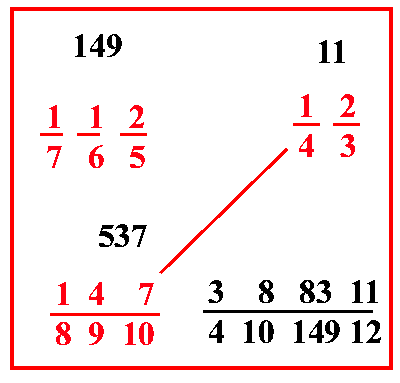 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Sui rotoli gerovini e forforini.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| (VIII.1.75; G: VIII.176) Ugualmente 1 62 513 rotoli gerovini si vendono per 1 71 53 bisanti, quanti rotoli forforini avrò avuto per 1 42 bisanti: poiché la vendita è di rotoli gerovini e la richiesta è di rotoli forforini, allora bisogna fare da 1 62 513 rotoli gerovini i rotoli forforini, cioè: moltiplicali per 1 62 e il totale che ne viene ponilo nel riquadro come vendita. E affinché si eviti il lavoro della detta moltiplicazione, poni 1 62 davanti a 1 62 513 rotoli, come più sopra abbiamo mostrato di fare in casi simili, e scrivi così il problema: e moltiplica il 2 per 6 e somma l'1, farà 13, ponilo sopra 1 62; e moltiplica il 13 per le sue frazioni, farà 407; e moltiplica il 3 per le sue frazioni, farà 117: dopo ciò moltiplica il 2 per il 4 e somma l'1, farà 9; ponilo sopra 1 42; e moltiplica il 9 per i numeri che sono di traverso ad esso, cioè per 13, e per 407, farà 47619; moltiplicalo per i rotti che sono sotto il 117, cioè per 5; e per 7; e dividi il totale per la regola di 117, che è 10 913 e per i numeri che sono sotto le linee di frazione dei numeri opposti, cioè per il 6 che sta sotto il 13, e per 5, e per 6 che stanno sotto il 407 e per il 4 che sta sotto il 9: ma se avrai voluto semplificare il lavoro del moltiplicare e del dividere, considera quando abbiamo detto: moltiplica il 9 per il 13 e lascia la loro moltiplicazione, poiché non li moltiplicherai, e non dividerai per 9, e per 13, che sono sotto la linea di frazione della divisione: perciò resta solo che moltiplichi 407 per i rotti, che sono sotto 117, e resta da dividere 1000 2589; dei quali lascerai di nuovo che non moltiplicherai per 5, che è sotto la linea sotto 117, e non dividerai per 5, che è sotto la linea della divisione: quindi moltiplicherai 407 per 7, che è sotto la linea sotto 117, e dividerai per 100 289, cioè per 100 2612. Per avere le once sopra il 12, faranno 129 261219 rotoli forforini, come è mostrato sopra nel riquadro. |
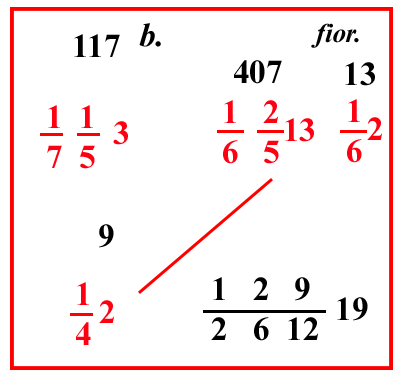
407×13×9×7×5
9×13×6×6×5×4 =
407×7
2×6×12
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Dello stesso al contrario.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
pg.102 |
(VIII.1.76; G: VIII.181) Ugualmente se si sarà detto che 1 92 512 di rotoli forforini valgono 3 44 bisanti; e che si chieda quanti rotoli gerovini avrà avuto qualcuno per 2 517 carati, cioè per 217 524 di un bisante: poiché un qualunque rotolo forforino è 6 13 di un rotolo gerovino, bisogna porre 6 13 [ davanti ] dopo 1 92 512 rotoli forforini, come si mostra in questo riquadro. E prenderai 1 92 512, e moltiplicherai 12 per le sue frazioni, farà 563: poi vai a 3 44, e moltiplicherai 4 per 4, e sommerai 3, farà 19: ancora moltiplicherai 17, che è sopra il 24, per 5, e somma 2, farà 87; e moltiplicherai 87 per 6, che si trova a lui di traverso sopra il 13; e per 563; e per 4, che è sotto la linea di frazione sotto il 19, e dividi il totale per 19,e per i numeri che sono sotto la linea di frazione dei numeri opposti, cioè per 5, e per 9, e per e per 13, e per 5, e per 24, cioè per 100000 5910131912; ed eviterai ciò che potrai evitare, e avrai per la quantità richiesta 13121010 510131912 di un rotolo gerovino. |
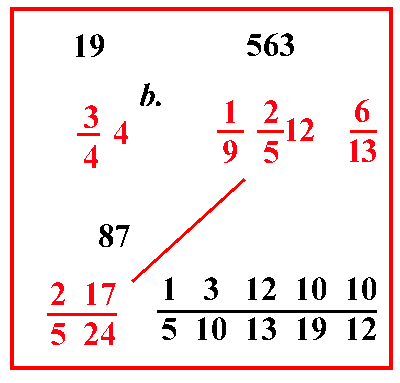 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Termina la prima parte dell'ottavo capitolo.
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||