pagina iniziale capitolo sesto parte terza del Liber abaci<br>Conv. Sopp. C.I. 2616, BNCF, folio 22 verso e 23 recto
parte terza cap VI
 
Parte Terza [NdT] Nel testo non compare la divisione tra
  la parte seconda e la parte terza che
  noi abbiamo ottenuto sulla base del
  contenuto dell’indice posto all’inizio
  del capitolo.

Sulla moltiplicazione dei numeri con due rotti sotto due linee di frazione
(VI.3.1 ; G: VI.47) Se vuoi moltiplicare 15, e un terzo e un quarto dell’uno intero, che si scrive così
1
4 
1
3
, con due linee separate, per un quinto e un sesto di 26, che si scrive così
1
6 
1
5
26
, scrivi l’argomento come qui si mostra, e moltiplica 15 per il 3 che è sotto la prima linea e aggiungi l’1, che è sopra il 3, farà un terzo di 46; moltiplicalo per il 4 che è sotto l’altra linea, farà 184 dodicesimi, al quale aggiungi la moltiplicazione dell’1 che è sopra il 4 per 3: poiché un quarto è uguale a tre dodicesimi, saranno in modo simile 187 dodicesimi, che poni nella dimostrazione sopra
1
4 
1
3
15
. Similmente moltiplica il 26 per i suoi rotti, cioè per 5, e aggiungi l’1 che è sopra il 5, [ farà 131 moltiplica per 6 e aggiungi 5 ] sarà 791 trentesimi, che poni sopra
1
6 
1
5
26
; e moltiplica 187 per 791, farà 147917; che dividi per tutti i numeri che sono sotto la linea di frazione, cioè per
1
0
0
0
3
4
5
6
 che, messi insieme, si convertono in
1
0
0
4
9
10
, farà
1
7
8
4
9
10
410
, come si vede nella dimostrazione.
⎧⎩15
+
1
3
+
1
4⎫⎭
×
⎧⎩26
+
1
5
+
1
6⎫⎭
15
+
1
3
+
1
4 = 15
×
3
+
1
3
+
1
4

187
1
4 
1
3
15
791
1
6 
1
5
26
1
7
8
4
9
10
410
pg.53 (VI.3.2 ; G: VI.49) Ancora, se vorrai moltiplicare
2
9 
3
5
16 con
2
11 
5
8
27
, scritto l’argomento, moltiplica 16 per 5 e aggiungi 3; moltiplica tutto questo per 9, e aggiungi la moltiplicazione del 2 che è sopra il 9 per il 5, farà 757, che poni sopra
2
9 
3
5
16
. Ugualmente moltiplica 27 per il suoi rotti, farà 2447 [NdT] 2 nel testo è un chiaro errore , moltiplicalo per 757, e dividi il totale per tutti i rotti, cioè per
1
0
0
0
5
8
9
11
, e uniti i rotti, farà
3
8
4
8
4
9
10
11
467. Se si vorrà fare la verifica di questa moltiplicazione con resto di 7, prendi il resto di
2
9 
3
5
16
, che si calcola così: si moltiplica il resto di 16, che è 2, per il 5 sotto la linea di frazione, e si somma il 3 che è sopra il 5, farà 13, il cui resto, che è 6, si moltiplica per il resto di 9 che è 2, farà 12; sopra il quale addiziona la moltiplicazione del 2, che è sopra il 9, per 5, farà 22, il cui resto, che è 1, è il resto di
2
9 
3
5
16
. E questo deve essere il resto di 757 e così è. Ugualmente trova il resto di
2
11 
5
8
27 che si trova così come l’abbiamo trovato con
2
9 
3
5
16
; e troverai che il suo resto è 4, che è il resto di 2447. Moltiplica quindi 1 per 4, farà 4, il quale 4 è il resto del totale, cioè di
3
8
4
8
4
9
10
11
467
.

757
2
9 
3
5
16
2447
2
11 
5
8
27
3
8
4
8
4
9
10
11
467

(VI.3.3 ; G: VI.51) E se vuoi ridurre
3
8
4
8
4
9
10
11
 nelle parti di un unico numero, moltiplica 11 per 10, e moltiplica il loro totale per 9, e tutto ciò per 4, farà 3960, numero chiamato denominatore: ponilo dunque sotto una linea di frazione, e moltiplica l’8 che è sopra l’11 per 10, e aggiungi il 4 che è sopra il 10; moltiplica tutto per 9 e aggiungi l’8 che è sopra il 9; [ moltiplica ] questo per 4 e aggiungi il 3, che è sopra il 4, farà 3059, questo numero è il numeratore. Perciò ponilo sopra la linea di frazione, e avrai
3059
3960
 [NdT] 2059 nel testo (e nel manoscritto)
  è un chiaro errore per ciò che è richiesto.
(VI.3.4 ; G: VI.53) Ancora se vuoi moltiplicare  [NdT] Nel testo per errore la linea
  di frazione è unica    1 9  1 8 17 per  1 17  1 3 28 , moltiplica gli interi per i loro rotti nell’ordine scritto sopra; e avrai per il numero superiore il numero 1241, e per l’inferiore il numero 1448; devi moltiplicare tra loro questi numeri e dividere il totale per tutti i rotti, cioè per 1
0
0
0  3
8
9
17  . E poiché
(PdA)
Il gerundivo ricorre nella perifrastica passiva, oltre a essere usato in funzione attributiva  [PdA,pag.12]
per la condivisione tra il numero da dividere e quello che divide, cioè tra i numeri che si moltiplicano tra loro e i numeri che sono sotto la linea di frazione, devi imitare il modo di semplificazione sopraddetto, cioè prendi  1 17 di 1241, cioè 73, al posto di uno dei numeri dalla moltiplicazione, per questo toglieremo il 17 che è sotto la linea. Ugualmente prendi  1 8 di 1448, cioè 181 al posto dell’altro; e togli  1 8 dalla linea di frazione. Quindi moltiplicherai 73 per 181, e dividerai il totale per i numeri restanti, che sono sotto la linea di frazione, cioè per  1
0   3
9   , farà  1
3   3
9  489 per la moltiplicazione richiesta: prenderai la prova del suo totale dalla prova di 73 e di 181; essendo il totale diviso dalla loro moltiplicazione. Infatti per  3 9 dirai  1 3 ; per  1
3   3
9  dirai  1 3 e un terzo di un nono.
 1 9  1 8 17 =  1241 9×8

 1 17  1 3 28 =  1448 17×3



1241 = 73 × 17
1448 = 181 × 8



 1
3  3
9 =
=  3 9 +  1 3×9 =  1 3 +  1 3×9
(VI.3.5 ; G: VI.55) Ancora abbiamo questo in qualche linea di frazione:  2
3
2
5   4
6
8
10   , che dirai in questo modo: per  5 10 dirai  1 2 ; e per  2 8 dirai la quarta parte di un decimo; e per  3 6 dirai un mezzo di un ottavo di un decimo, e per  2 4 dirai la metà di un sesto di un ottavo di un decimo; e queste sono in relazione per ciò che i numeri superiori hanno in comune con gli inferiori.
 2
3
2
 5   4
6
8
10  =
=  5 10 +  2  8×10 +  3   6×8×10 +  2    4×6×8×10 =
=  1 2 +  1  4×10 +  1   2×8×10 +  1    2×6×8×10
(VI.3.6 ; G: VI.55-56) Ed è da notare che
(PdA)
Sono abituali nel Liber abbaci le dichiarative introdotte da quod o quia (assai diffuse già nel sec. IV d.C. anche nella lingua letteraria), talora costruite con il congiuntivo  [PdA,pag.10]
molte frazioni, che sono sotto linee diverse, possono essere ridotte ad una sola linea di frazione, cioè alle parti di un solo numero come sarà dimostrato a suo luogo. Ma qui ho ritenuto necessario mostrare in quale modo si uniscono due fazioni che sono sotto due linee: moltiplica il numero sotto la prima linea per il numero sotto la seconda; e ciò che risulta ponilo sotto una linea: poi moltiplica il numero sopra la prima linea per il numero che è sotto la seconda; e il numero che è sopra la seconda per il numero che è sotto la prima; unisci queste due moltiplicazioni; e poni ciò che ne verrà sopra la linea di frazione, e avrai ciò che hai cercato. Per esempio: vogliamo sommare  1 2 con  2 5 , moltiplica il 2 per il 5 che sono sotto la linea, farà 10, che poni sotto una linea; e moltiplica l’1 che è sopra il 2 per 5, e il 2 che è sopra il 5 per il 2 che è sotto la linea, farà 5 e 4, cioè 9 : questo 9 ponilo sopra la linea, e avrai  9 10 in luogo di  2 5  1 2 . Altrimenti fa i decimi dall’uno intero, saranno 10 decimi: perciò per  1 2 avremo  5 10 , e per  2 5 avremo  4 10 ; e così per  1 2 e  2 5 avremo  9 10 , come abbiamo detto.
somma di frazioni




 2 5  1 2 =  1 2 +  2 5 =  5 + 4 10


 1 2 +  2 5 =  5 10 +  4 10 =  9 10

pg.54 		(VI.3.7 ; G: VI.58-59) E sebbene in questi due modi si possano ridurre due frazioni di due linee a una sola linea, tuttavia insegnerò come procedere in modo più diretto con le frazioni che hanno sotto la linea numeri comunicanti [ con fattori in comune ]. Così se vorrai ridurre a una sola frazione  2 9   1 3 , poiché 3 e 9, che sono sotto la linea, sono comunicanti fra loro e il loro numero comune è il 3, dividi uno di questi numeri, cioè 3, o 9, per 3, cioè per la loro misura comune e moltiplica ciò che ne risulta per l’altro numero, e risulterà 9 come denominatore. Per esempio: moltiplicata la terza parte di 3 , cioè 1, per 9, o moltiplicata la terza parte di 9 per 3, sicuramente da qualunque moltiplicazione risulta il predetto 9: ponilo sotto una linea di frazione, e moltiplica 1, che è sopra il 3, per la terza parte di 9, farà 3 che conservi in mano; e moltiplica il 2 che è sopra il 9 per la terza parte di 3, cioè per 1, farà 2; che aggiungi al 3 serbato, farà 5; che poni sopra la linea sotto la quale è posto il 9, e avrai  5 9  per  2 9   1 3 . Introduce il minimo comune multiplo

 1 3 +  2 9 =  3 + 2 9 =  5 9
(VI.3.8 ; G: VI.61) Ancora, vogliamo addizionare  5 6   3 4 : poiché il due è in comune al 4 e al 6, moltiplica la metà di 4 per 6, e avrai 12; che poni sotto una qualche linea, e moltiplicherai il 3 che è sopra il 4 per la metà di 6, e quello che è sopra il 6 per la metà di 4; e avrai 9 e 10, che congiungi insieme, farà 19; questo 19 dovrebbe essere posto sopra il 12 posto sotto la linea se fosse minore di 12, ma poiché è maggiore, dividi 19 per 12, farà  7 12 1 per la congiunzione di  5 6  3 4 . E bada che quando sotto due linee si pongono numeri comunicanti, o dalla loro moltiplicazione non risulta un numero maggiore di dieci, allora per la detta dottrina devi ridurre le frazioni stesse ad un'unica linea di frazione e averla al posto di quelle due stesse linee, come mostrerò in seguito. Ma prima porrò nelle tavole sottoscritte due frazioni che devi unire; e davanti ad esse porrò la loro unione, e comincerò da  1 2 e  1 2 che fa 1: e poi seguiranno  3 2  1 2 che fa  5 6 ecc., come è scritto nelle tavole seguenti.
 3 4 +  5 6 =  3×3 + 5×2 12




 19 12 =  7 12 1


tavola
somme frazioni
python 		(VI.3.8-tab1 ; G: VI.63)



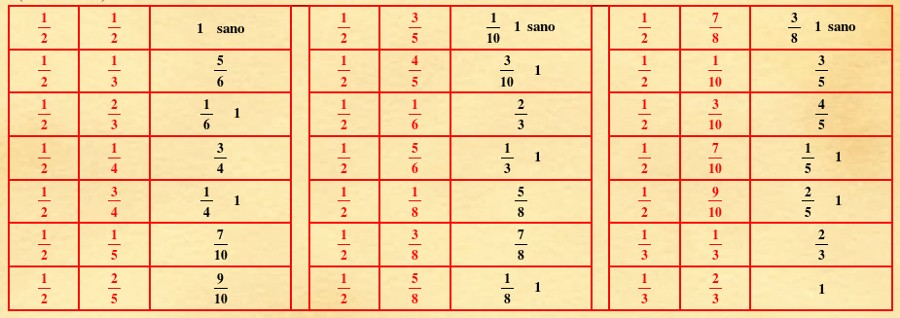
pg.55 		(VI.3.8-tab2) [NdT] Nella tabella abbiamo corretto
  evidenti errori di calcolo.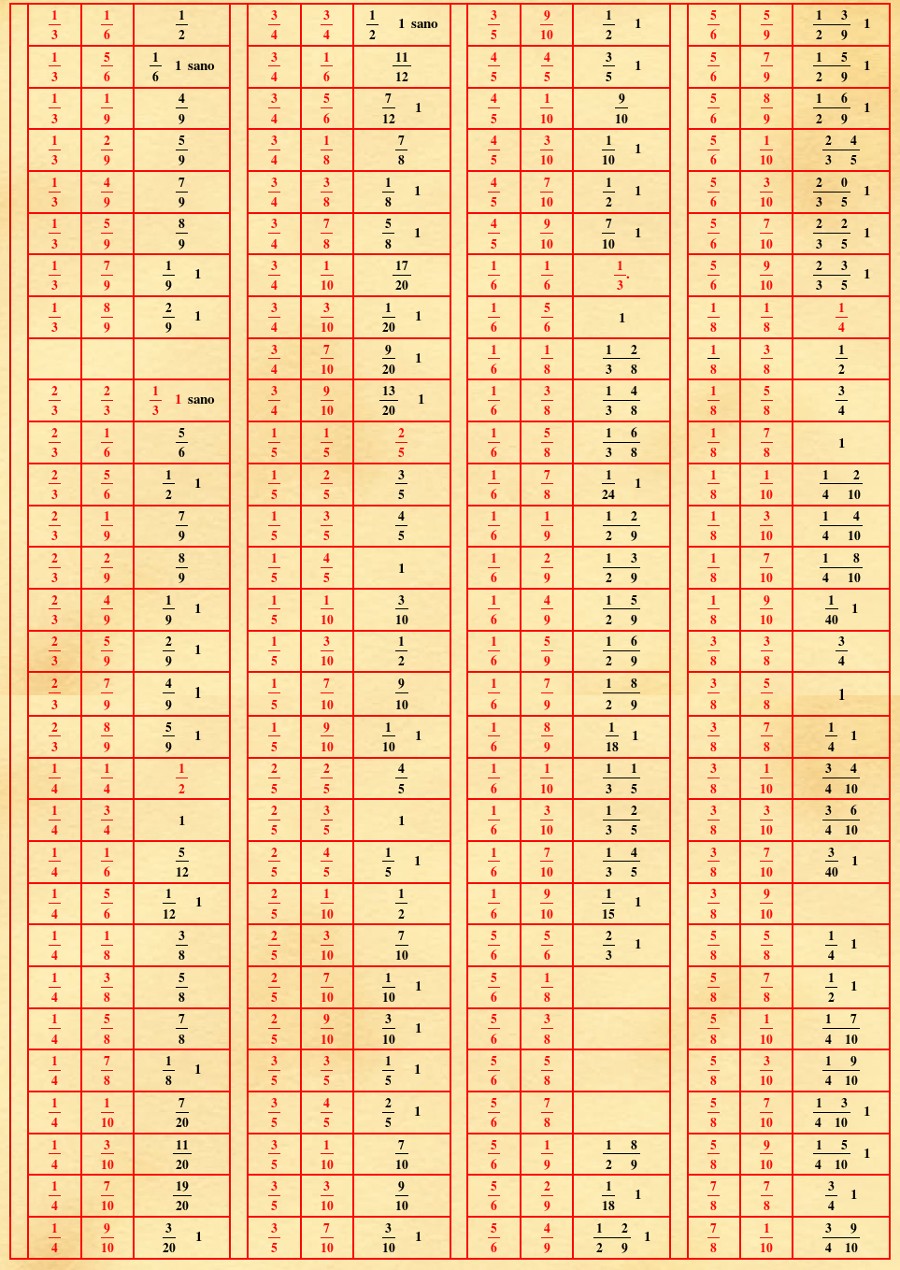



pg.56 		(VI.3.9 ; G: VI.69) C onosciute così le suddette unioni delle frazioni, se sarà proposto di moltiplicare  1 3  1 2 11 per  1 5  1 2 22: moltiplicherai  5 6 11 per  7 10 22. Ugualmente se vuoi moltiplicare  5 6  3 4 12 per  1 9  2 3 23 somma prima  3 4 con  5 6 , farà  7 12 1, cioè  1
3   2
6   1; che sommi con 12, farà  1
3   2
6   13: similmente somma  2 3 e  1 9 , farà  7 9 : quindi moltiplicherai  1
3   2
6   13 per  7 9 23; e così si intenda in seguito.

Termina la terza parte del sesto capitolo.




×