progetto fibonacci - traduzione-05-testo

Comincia il quinto capitolo sulla divisione di numeri interi

pg.24

(V.1 ; G: V.1) Per coloro che vogliono saper dividere qualsiasi numero per qualsiasi numero è a loro necessario che imparino prima a dividere tutti i numeri per i numeri che vanno da due fino a dieci; e poiché non possono saperlo, fino a quando non sappiano tenere a mente i riquadri delle divisioni di alcuni numeri per gli stessi, sappiano che le divisioni di questi sono mostrate in tabelle nelle pagine seguenti. Ma prima si insegni come scrivere in modo perfetto tutti i numeri rotti.

(V.2 ; G: V.2) Quando su un qualsiasi numero sia stata tracciata una qualche lineetta, e sopra la stessa lineetta sia stato scritto un qualunque altro numero, il numero superiore indica la parte o le parti del numero inferiore; infatti il numero inferiore è chiamato denominato [ denominatore ] e quello superiore è chiamato denominante [ numeratore ] . Così se sopra al numero 2 sia stata tracciata una linea, e sopra di essa sia scritta l’unità, questa unità attesta una parte delle due parti dell’uno intero, cioè la metà così: 1 2 e se l’unità fosse stata posta sopra al numero 3 così: 1 3 denota la terza [ parte ]; e se sopra al numero 7 così: 1 7 la settima; e se sopra al 10, la decima, e se sopra al 19, intende una diciannovesima parte dell'uno intero, e così di seguito. Ancora se 2 è stato messo sopra il 3 così , 2 3 intende due parti delle tre parti dell’uno intero, cioè due terzi. E se è sopra il 7 due settimi così: 2 7 e se sopra il 23 indicheranno due ventitreesimi, e così via. Ancora se il sette sia stato posto sopra il nove così , 7 9 indica sette noni dell’uno intero; e se il sette è sopra il 97, denoterà sette novantasettesimi. Ancora il 13 posto sopra il 29, indica tredici ventinovesimi. E se 13 è sopra 347, indicherà tredici trecentoquarantasettesimi, e così è da intendere per i restanti numeri.

Il significato di
numeratore e
denominatore.

frazioni multiple

(V.3 ; G: V.6) Ancora se sotto una stessa linea siano stati posti più numeri, e sopra ciascuno di quegli stessi si scriveranno altri numeri, il numero che sia stato posto sopra il numero all’inizio della parte destra della linea, indicherà la parte o le parti del numero stesso posto sotto, come abbiamo già detto. Quello dunque sopra il secondo esprime le parti dello stesso secondo delle parti del primo numero posto sotto. Quello poi sopra il terzo indica le parti di questo terzo delle parti del secondo delle parti del primo, e così sempre quelli che seguiranno sopra la linea denotano le parti di tutte le parti precedenti sotto la linea, così, se sotto una qualche linea ci sono 2 e 7 e sopra il 2 ci sia 1 e sopra il 7 ci sia 4 come qui si vede

, si denotano quattro settimi e la metà di un settimo. Se però sopra il 7 ci fosse zero, così :

, si indicherebbe solo la metà di un settimo.

Introduce le frazioni multiple

...a₃ a₂ a₁ ...b₃ b₂ b₁ =
= a₁ b₁ + a₂ b₁ b₂ + a₃ b₁ b₂ b₃ + ...

= 4 7 + 1 14 = 9 14

(V.4 ; G: V.9) Ancora, sotto una qualche altra linea ci siano 2, 6 e 10 e sopra il 2 ci sia 1 e sopra il 6 ci sia 5 e sopra il 10 ci sia 7, come qui si mostra

il sette che è sopra il 10 all’inizio della linea rappresenta sette decimi , e il 5 che è sopra il 6 indica cinque sesti di una decima parte, e l’1 che è sopra il 2 indica la metà della sesta parte di un decimo e così uno ad uno s’intenda di ognuno: tuttavia bisogna avvisare che i numeri più piccoli sono sempre verso sinistra sotto una stessa linea: ma se ci fossero più linee, i rotti di una linea non rispondono ai rotti di un’altra, e quella frazione che è la maggior parte dell’intero, deve essere sempre posta verso la mano destra. Inoltre le frazioni, che sono in una sola linea, sono dette essere in posizione, e la prima posizione di quelle è la frazione che è all’inizio della linea nella parte destra. La seconda posizione è la frazione che segue verso sinistra. Per esempio, nella linea scritta sopra, cioè in

, 7 10 sono nella prima posizione di questa linea e 5 6 sono in seconda e 1 2 è nella terza, cioè nell’ultima posizione della medesima frazione, e così quanti sono i numeri sotto la linea, tante sono le posizioni della stessa.

=
= 7 10 + 5 60 + 1 120 = 95 120

Frazioni multiple graduate

(V.5 ; G: V.12) E se nella linea ci saranno più rotti e questa linea sarà terminata con un cerchietto, allora le sue frazioni indicheranno altro di quanto è stato detto, come in questa linea:

o , le cui frazioni indicano otto noni di un intero e sei settimi di otto noni, e quattro quinti di sei settimi di otto noni e due terzi di quattro quinti di sei settimi di otto noni dell’ uno intero. E se questa linea terminasse dall’altra parte con il cerchietto, così: o

, denoterebbe solo due terzi di quattro quinti di sei settimi di otto noni dell’uno intero. Ancora se dei trattini si prolungassero sulla linea in questo modo

, le sue frazioni denotano cinque noni e un terzo e un quarto e un quinto di un nono. Comprese così queste cose, come si vede sotto, si scrivano i riquadri predetti imparandoli a mente con grande studio.

Introduce vari tipi di frazioni

⋯ a₃ a₂ a₁ ⋯ b₃ b₂ b₁ o =
= a₁ b₁ + a₂ b₂ × a₁ b₁ + a₃ b₃ × a₂ b₂ × a₁ b₁ + ⋯

o a_n ⋯ a₃ a₂ a₁ b_n ⋯ b₃ b₂ b₁ =
= a_n b_n × ⋯ × a₃ b₃ × a₂ b₂ × a₁ b₁

=
= 5 9 + ( 1 3 + 1 4 + 1 5 ) × 1 9 = 347 540

(V.5.Tab1 ; G: V.14)

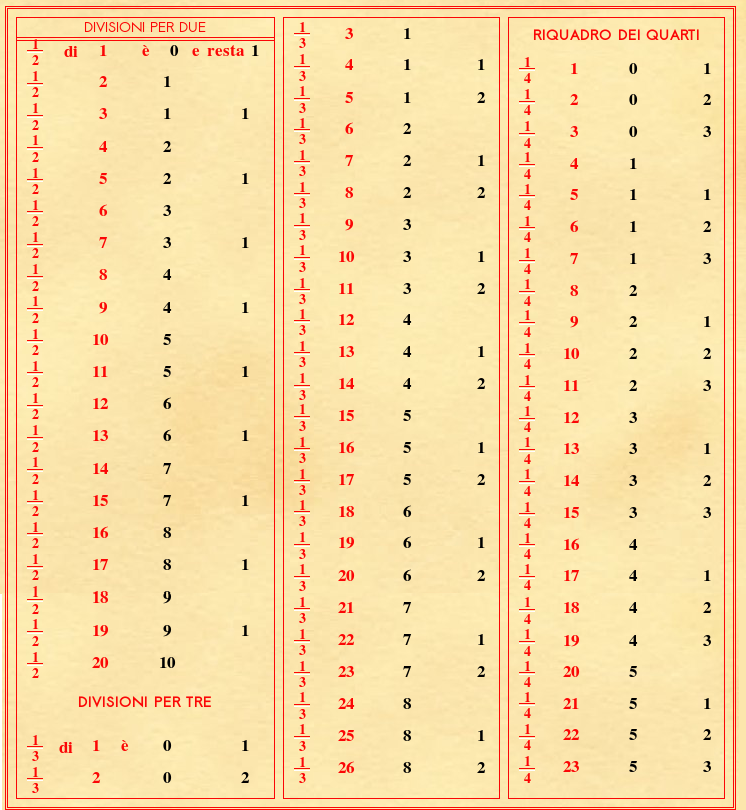
pg.25

(V.5.Tab2)

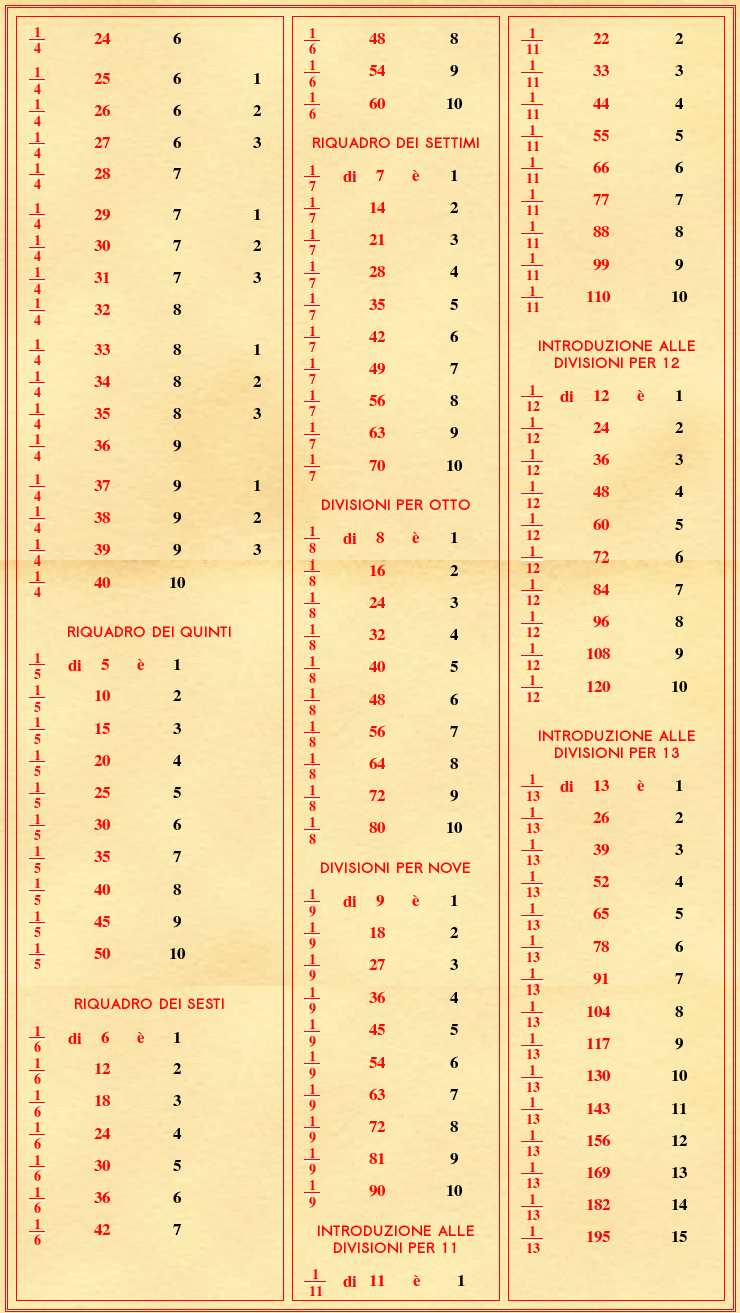
Regola generale della divisione dei numeri per i numeri di prima posizione.

algoritmo divisione

(V.6 ; G: V.25) Conosciute dunque le divisioni scritte sopra e approfondite in modo ottimo con un frequente esercizio di ciò e se qualcuno volesse dividere qualunque numero di qualunque posizione per uno qualunque dei numeri suddetti, cioè di quelli che vanno da due fino a dieci, scriva il numero sulla tavola, e ponga la figura, figura per la quale abbia voluto dividere il numero, sotto la prima posizione del numero stesso; e inizi la divisione dall’ultima figura del numero e la divida, se sarà possibile, per il numero della figura per la quale abbia voluto dividere il numero, ponendo [ il quoziente della ] divisione più in basso sulla tavola sotto la medesima ultima posizione: e se dalla divisione avanzasse qualcosa, ponga tale avanzo sopra la medesima ultima figura; e lo unisca con figura successiva, e divida queste due figure, come se formassero un numero di due figure, e ponga il quoziente della divisione sotto la stessa figura successiva; e se ci fosse un avanzo, lo scriva sopra di essa. E così, unendo sempre nell’ordine qui sopra descritto, l’avanzo alla figura seguente, e ponendo il numero che sia risultato dalla divisione, e scrivendo l’avanzo più in su, procedendo passo a passo, si giungerà fino alla prima figura del numero.

Come si esegue la divisione di un qualsiasi numero intero per un numero di una cifra

(V.7 ; G: V.27) In verità, poiché spesso succede che le figure per le quali i numeri saranno divisi siano maggiori delle ultime figure degli stessi numeri, allora, non essendo possibile dividere questo numero per quelle, cominci la divisione dalle ultime figure, e da quelle successive; e le divida unite nel modo sopra descritto, e ponga il quoziente sotto le penultime, e proceda a calcolare, come abbiamo detto precedentemente, dagli avanzi fino alla fine: se non ci sarà un avanzo qualunque, divida solo la figura stessa, che si insegna ad unire finché si troverà l’avanzo: e se non potrà dividere quella figura, perché è minore di quella stessa per la quale si divide, ponga sotto di essa uno zero, e la aggiunga tutta intera come avanzo unendola alla figura successiva; e così avrà le quantità di qualunque delle dette divisioni.

(V.8 ; G: V.29) Così, se volesse dividere 365 per 2, scriva il 2 in una parte della tavola, e vi tracci sopra una linea e ponga un altro 2 sotto il 5, e cominci a dividere 3 per 2, cioè l’ultima figura, dicendo di 3 è 1, e rimane 1: scriva 1 sotto lo stesso 3 e scriva più in alto l’1 che resta, come si vede nel primo riquadro ; e l’1 rimanente unito con il 6, che è posto accanto all’ultima figura suddetta, farà 16: prenda 1 2 di 16 che è 8; ponga dunque l’8 sotto il 6 anteposto, l’1 sotto il 3, come si vede nel secondo riquadro; e poiché non è avanzato nulla nella divisione di 16, divida il 5 per 2: sarà 2 e rimane 1: scriva il 2 sotto il 5 e scriva l’1 che resta sopra il 2 posto che raccomandammo di conservare a parte con la linea [ di frazione]; e sarà la metà di uno intero: e davanti a questo 1 2 [ cioè a seguire ] scriva il numero che proviene dalla divisione, cioè 182, come si vede nell’ultimo riquadro .

	1
	3	6	5
			2
2	1

	1
	3	6	5
			2
2	1	8

	1
	3	6	5
			2
1 2	1	8	2

(V.9 ; G: V.31) Infatti i rotti o i fratti si devono porre sempre dopo gli interi [ cioè a sinistra ], anche se si devono riferire prima gli interi che i rotti. Ed è da notare inoltre che quando un numero è diviso per un altro numero, allora dalla moltiplicazione del divisore per il risultato ne viene il numero diviso. Per esempio se si divide 40 per 4, risulta 10. Per cui se moltiplichiamo 4 per 10, si ha quaranta, vale a dire il numero diviso. Allo stesso modo se si moltiplicherà 1 2 182 per 2, cioè il numero che esce [ dalla divisione ] per il divisore, farà 365, vale a dire il numero diviso.

Verifica che
( 1 2 182 ) x 2 = 365

pg.28

(V.10 ; G: V.32) Parimenti se volesse dividere ancora 365 per 3 , scriva il 3 sotto il 5 e divida 3 per 3, farà 1, che ponga sotto il 3. Parimenti divida 6 per 3, farà 2 che ponga sotto il 6; e divida 5 per 3, farà 1 e ne rimarrà 2: ponga 1 sotto il 5 e 2 sopra la linea di frazione del 3 dalla parte conservata, e davanti ad essa ponga il numero che esce dalla divisione, cioè 121 e così si avrà 2 3 121 per la divisione richiesta, come qui si mostra. E sia da notare che il numero che è diviso si chiama diviso o dividendo, e il numero che divide è chiamato dividente o divisore e il numero che risulta dalla divisione si chiama procedente o uscente.

	1
	3	6	5
			3
2 3	1	2	1

Divisione di 1346 per 4

(V.11 ; G: V.33) Parimenti se qualcuno volesse dividere 1346 per 4, ponga il 4 sotto il 6 e divida il 13 per 4, dal momento che non è possibile dividere l’1, che è nell’ultima posizione del numero, farà 3 e ne rimarrà 1: ponga il 3 sotto il 3 e ponga l’1 che resta sopra lo stesso 3, e unisca l’ 1 stesso con il 4 che precede il 3 nel numero, verrà 14: prenda la quarta parte di 14 che è 3 e rimane 2: ponga il 3 più in basso sotto il 4 e il 2 che resta più in alto, che unito con il 6, fanno 26; che divida per 4, farà 6 e ne rimarrà 2: ponga il 6 sotto il 6 e ponga il 2 del resto sopra la linea del 4 conservato da parte che indica due quarti dell’ uno intero, che sono uguali alla metà dell’ uno intero; e davanti ad esso ponga il numero uscente dalla 1 2 336 per la divisione richiesta.

	1	2
1	3	4	6
			4
2 4 = 1 2	3	3	6

(V.12 ; G: V.35) Per esempio: abbiamo diviso prima 13 per 4, e questo 13 termina in terza posizione. Per questo sappiamo che è un numero delle centinaia, poiché la terza posizione è delle centinaia. Divise dunque tredici centinaia per 4, si hanno tre centinaia e resta un centinaio indivisibile. Per questo abbiamo posto il 3 in terza posizione, cioè nel posto delle centinaia, e abbiamo messo l’1, che era avanzato, sopra il 3 e anche denota cento; e abbiamo unito questo 1 con il 4, diventò 14 che termina in seconda posizione, cioè nel posto delle decine. Per questo indica un centinaio e 4 decine che abbiamo diviso per 4, sono risultate tre decine, e sono rimaste due decine indivisibili: per questo abbiamo posto il 3 sotto il 4 e il 2 sopra il 4, naturalmente nel luogo delle decine, e abbiamo unito questo 2 con il 6 della prima posizione. Dall’unione di questi numeri abbiamo ottenuto 26 unità; poiché questa unione termina in prima posizione; e abbiamo diviso queste 26 unità per 4, e sono risultate 6 unità, e il resto è di 2. Per questo abbiamo posto il 6 nel luogo delle unità, e abbiamo posto il due sopra la linea del 4; e così s’intenda per le altre divisioni simili.

Divisione di 5439 per 5

(V.13 ; G: V.37) Parimenti, se qualcuno volesse dividere 5439 per 5, ponga il 5 sotto il 9 e dica: 1 5 di 5, è 1, che ponga sotto il 5 e 1 5 di 4 è 0, e resta 4: ponga lo 0 sotto il 4, e riguardo al 4 restante, unisca questo stesso 4 col 3 e dica: 1 5 di 43, è 8 e rimane ancora 3: ponga l’8 sotto il 3 prenda la quinta parte di questo 3 unito al 9, cioè di 39, farà 7 e resta 4: ponga il 7 sotto il 9 e il 4 sopra la linea del 5 conservato a parte e ponga avanti il numero uscente dalla divisione.

		4	3
	5	4	3	9
				5
4 5	1	0	8	7

Divisione di 9000 per 7

(V.14 ; G: V.38) Ancora, se si volesse dividere 9000 per 7, si ponga 7 sotto il primo zero, e si divida 9 per 7, farà 1 e resta 2: si ponga quindi 1 sotto il 9 il 2 sopra, questo 2 unito con lo 0, che è subito dopo il 9, fa 20 che si divida per 7, farà 2 e rimane 6: si ponga 2 sotto quello zero e il 6 al di sopra, questo unito con lo zero seguente fa 60 che si divida per 7, farà 8 e resta 4: si ponga 8 sotto quello zero 0, e si ponga 4 al di sopra, che unito con lo zero in prima posizione fa 40, che si divida per 7, farà 5 e resta 5: si ponga 5 sotto lo stesso 0 e il rimanente 5 si ponga sopra la linea del 7 tracciata a parte, e davanti ad essa si ponga il numero risultato dalla divisione.

	2	6	4
	9	0	0	0
				7
5 7	1	2	8	5

Divisione di 10000 per 8

pg.29

(V.15 ; G: V.39) Ancora, se si volesse dividere 10000 per 8, si ponga 8 sotto lo 0 in prima posizione e si dica: 1 8 di 10 è 1 con resto 2: si ponga 1 [ sotto lo 0 in quarta posizione e si stabilisca: 1 8 di 20 è 2 con resto 4, si ponga il 2 ] sotto lo 0 in terza posizione e sopra si ponga il 4 e si prenda 1 8 di 40 è 5 che si ponga sotto la seconda posizione; e per completare l’ordine delle posizioni del numero risultante, bisogna porre 0 sotto lo 0 in prima posizione, come si vede in questo riquadro.

	2	4
1	0	0	0	0
				8
	1	2	5	0

Divisione di 120037 per 9

(V.16 ; G: V.40) Ugualmente se si volesse dividere 120037 per 9, si scriva il 9 sotto il 7 e si dica: 1 9 di 12 è 1 e resta 3: si ponga 1 sotto il 2 e al di sopra il 3, e 1 9 di 30 è 3 e resta 3: si ponga 3 sotto lo 0 in quarta posizione e sopra si ponga 3; e di nuovo si prenda 1 9 di 30 che è 3 e resta 3: si ponga 3 sotto lo 0 in terza posizione e si ponga il 3 sopra lo stesso 0: di nuovo di 33 è 3 e resta 6: si ponga il 3 sotto il 3 e sopra il 6 e 1 9 di 67 è 7 e resta 4: si ponga il 7 sotto il 9 e il 4 che resta si ponga sopra la linea del 9 scritta da parte. E così se si saprà dividere secondo l’ordine del dividere scritto sopra non si potrà mai sbagliare in nessuna divisione simile: nello stesso modo si possono dividere tutti i numeri anche per 11 e per 13: tuttavia occorre innanzitutto conoscere le presentazioni degli stessi altri ordini scritti sopra, come sono contenuti nelle tabelle delle divisioni più sopra. Infatti la presentazione dell’11 sale da 1 fino a 11 decine, cioè a 110. E la presentazione del 13 sale da 1 fino a 13 decine, cioè a 130.

		3	3	3	6
	1	2	0	0	3	7
						9
4 9		1	3	3	3	7

Divisione dei numeri per 11

(V.17 ; G: V.42) Conosciute appunto le dette presentazioni, e qualcuno volesse dividere 12532 per 11, ponga l’11 sotto il 32. Prenda 1 11 di 12, che è in testa al numero da dividere che è 1, e resta 1. Perciò, poiché di 1 11 di 11 è 1 come si vede nelle tavole scritte sopra, , allora 1 11 di 12 è 1 e resta 1. Poni così l’1 sotto il 2 dello stesso 12 e l’1 che rimane ponga sopra il 2, e unisca lo stesso 1 con la figura antecedente, cioè col 5, farà 15, dal quale prenda 1 11 che è 1 e resta 4 per il detto calcolo; e ponga 1 sotto il 5 e il restante 4 sopra il 5 che unisca con la figura antecedente, cioè con 3, che farà 43: dal quale ancora si prenda 1 11 che è 3 e resta 10: e perciò, 1 11 di 33 è 3, per arrivare da questo a 43 è 10: quindi 1 11 di 43 è 3 e resta 10, come abbiamo detto: ponga dunque il 3 sotto il 3, e ponga il 10 sopra il 43, cioè ponga 1 sopra a 4, che era stato posto sopra il 5 e pone 0 sopra 3 e unisca inoltre questo dieci con la figura antecedente, cioè con 2 che è in prima posizione, sarà 102, dai quali ancora si prenda , sarà 9 e resta 3: ponga il 9 sotto il detto 2 e il restante 3 lo ponga sopra la linea dell’11 conservato a parte, e avrà per la divisione richiesta 3 11 1139

		1
	1	4	0
	1	2	5	3	2
				1	1
3 11		1	1	3	9

Divisione di 123586 per 13

(V.18 ; G: V.45) Ugualmente se si volesse dividere 123586 per 13, posto il 13 sotto 86, si divida 123 per 13; essendo 12 più piccolo di 13, farà 9 con resto 6. Infatti la tredicesima [ parte ] di 117 è 9, dal quale [ per arrivare ] fino a 123 manca 6: si ponga 9 sotto il 3 dello stesso 123 e 6 che resta si ponga sopra lo stesso 3 e lo si unirà al 5, sarà 65, di cui 1 13 è 5: perciò si ponga il 5 sotto il 5 e sotto l’8 si ponga 0, essendo 8 minore di 13, e questo stesso 8 si unirà al 6 che è in prima posizione, sarà 86, essendo 6 1 13 di questo e resta 8: si pone 6 in prima posizione del numero risultato, e 8 sopra la linea del 13, e si avrà per la divisione richiesta 8 13 9506: in questo stesso modo i numeri possono essere divisi anche per 17 e per 19; tuttavia occorre conoscere le presentazioni degli stessi secondo l’ordine degli altri numeri scritti sopra. Ma poiché sembra pesante tenere a mente le presentazioni degli stessi, mostreremo a suo tempo come si dividano i numeri per 17 e per 19 in un altro modo, e anche per gli altri numeri di due figure.

			6
	1	2	3	5	8	6
					0
					1	3
8 13			9	5	0	6

La divisione dei numeri con la mente e con le mani per gli stessi numeri

pg.30

(V.19 ; G: V.47) Pur tuttavia se si volesse operare la materia di simili divisioni tenendo a mente nelle mani, si conservi in mano il numero che si vorrà dividere, e si vada avanti sempre con le mani, dividendo passo a passo, cominciando dall’ultima figura, ponendo sempre nelle mani i numeri derivati dalla divisione, tendendo sempre a mente gli avanzi; e cancellando gradualmente dalle mani il numero da dividere. Per esempio: se si fosse proposto di dividere 7543 per 6, si tenga nelle mani il numero scritto prima e divida 7 per 6, il 7 che è nella mano destra nel posto delle migliaia, farà 1 e resta 1: cancelli 7 dalla mano e vi ponga 1, e tenga a mente l’1 che rimane, che unisca col 5 che è nella mano destra nel posto delle centinaia, sarà 15 che divida per 6, farà 2 e resta 3: cancelli 5 dalla mano e ponga nello stesso posto 2 e tenga 3 in mente; questo unito al 4 che è nella mano sinistra nel posto delle decine , farà 34, che divida per 6, farà 5 col resto di 4: cancelli 4 dalla mano e ponga nello stesso posto il 5 e tenga a mente il 4 rimasto, che unisca col 3 che è nella medesima mano nel posto delle unità, sarà 43 che divida per 6, farà 7 e resta 1: cancelli 3 dalla mano e vi ponga 7 nello stesso luogo, e per l’1 che resta determini 1 6 ; e così si avrà in mano per la divisione richiesta 1 6 1257.

7543 diviso 6
con le mani

Divisione di 8059 per 5

(V.20 ; G: V.50) Oppure se si volesse dividere 8059 per 5, si tenga il numero in mano e si determini: 1 5 di 8 che è nella posizione delle migliaia è 1 e resta 3: cancelli 8 dalla mano e ponga nello stesso posto 1, e tenga a mente 3; e poiché in questo numero nella posizione delle centinaia non si ha nulla mano, si deve dire che lì vi sia lo zero, a cui si aggiunge il 3 serbato, farà 30, 1 5 del quale è 6 che si tenga a mente nel posto delle centinaia; e porti la divisione dalla mano destra alla sinistra, determinando 1 5 di 5, cioè di quello che è nella posizione delle decine, è 1: cancelli 5 e vi ponga 1 e prenda 1 5 di 9, cioè da quello che è nella posizione delle unità, che è 1 e tenga il 4: cancelli lo stesso 9 dalla mano e vi ponga nello stesso posto 1 e per il restante 4 si determini 4 5 ; e così si avrà come risultato della divisione richiesta 4 5 1611, e così si intenda nelle restanti divisioni simili.

8059 diviso 5
con le mani

(V.21 ; G: V.52) Se poi qualcuno volesse dividere un numero qualunque per 10, tolga dal numero stesso la figura in prima posizione e la ponga sopra il 10 messo da parte con la linea [ di frazione ], e davanti ad essa ponga il numero che sarà rimasto dopo la cancellazione della detta prima figura; e così si potrà dividere qualunque numero per 10. Per esempio: se si volesse dividere 167 per 10, si cancelli da questo la figura in prima posizione, cioè 7 e la si ponga sopra quel 10, come abbiamo detto, dalla parte serbata con la linea di frazione, e prima di questa si ponga il numero restante, cioè 16; e così si avrà come risultato della divisione richiesta 7 10 16. E se si volesse dividere 1673 per 10 si cancelli il 3 da 1673, rimanendo per questa divisione 3 10 167.

Divisione per 10

Iniziano le divisioni dei numeri per numeri non composti di seconda posizione

pg.31

(V.22 ; G: V.53) Alcuni numeri sono non composti, e sono quelli che in aritmetica e in geometria si chiamano primi. Questo perché non possono essere misurati o numerati da nessun numero esistente minore ad essi all’infuori dell’unità. Gli Arabi li chiamano hasam. I Greci coris canon

^(PdA)

La notizia che i Greci dicessero i numeri primi coris canonos, cioè chorìs kanònos, ovvero ‘senza misura di riferimento’, sarà giunta a Leonardo attraverso una fonte recenziore, forse la stessa che gli forniva la denominazione araba hasam. [PdA,pag.5]

, noi invece li chiamiamo senza regole; quelli di loro che sono fino a cento sono scritti in una tabella nel seguito. Poi insegnerò a trovare con una regola gli altri primi, che sono dopo il cento. I numeri restanti invece sono chiamati composti o epipedi, cioè piani da Euclide espertissimo di geometria. Questo perché sono composti dalla moltiplicazione di alcuni numeri, come il dodici che è composto dalla moltiplicazione di due per 6, o di tre per 4, noi invece li chiamiamo numeri regolari. E poiché la dottrina del dividere per i numeri primi e per quelli composti non è la stessa, mostriamo come prima cosa come dividere qualunque numero che sia maggiore di questi, cioè per quelli che sono senza regole più piccoli di cento.

Definizione di numero primo

I numeri regolari sono quelli decomponibili in fattori e la

tabella numeri primi

11	37	67
13	41	71
17	43	73
19	47	79
23	53	83
29	59	89
31	61	97

(V.23 ; G: V.55) Se allora qualcuno volesse dividere un numero qualsiasi per un numero qualunque di quelli scritti sopra, che siano senza regola, scriva il numero sulla tavola e sotto di esso ponga il numero primo stesso per il quale voleva dividere, collocando (se mai)ogni posizione simile sotto alla simile, e veda se le due ultime figure del numero da dividere faranno un numero più grande, o uguale, o minore dello stesso numero primo per il quale il numero sarà diviso. E se faranno un numero maggiore o uguale, l’ultima posizione del numero risultante deve cominciare sotto l’ultima posizione successiva (la posizione che segue l’ultima) del numero da dividere, cioè sotto la penultima, e proprio lì ponga a giudizio tale figura, che moltiplicata per quel numero divisore, faccia come risultato il numero delle due ultime figure dette prima, o pressappoco.

Divisione per un numero primo di due cifre

(V.24 ; G: V.57) E allora moltiplicherà questa per l’ultima figura dello stesso numero primo, cioè del divisore, e sottragga il risultato dall’ultima figura. E se dovesse avanzare qualcosa, scriva l’avanzo sopra la figura stessa. E moltiplichi la stessa figura posta per la prima dello stesso numero primo, cioè del divisore, e sottragga la moltiplicazione dall’unione del detto avanzo e della penultima figura, e se il resto fosse un numero di due figure, cioè più grande di 10, ponga la prima posizione di quel numero sopra la penultima figura, e l’ultima sopra l’ultima. Se poi questo avanzo fosse in prima posizione, cioè minore di 10, ponga la figura dello stesso sopra la penultima, e unisca questo avanzo con la terza figura dall’ultima. E sotto questa terza figura ponga a giudizio tale figura, che moltiplicata per lo stesso divisore dia il numero di detta unione, o quasi: come sia questo giudizio, si abbia dalla perizia; farò in modo di mostrare nelle seguenti divisioni, secondo le loro differenze.

(V.25 ; G: V.58) E allora moltiplichi la stessa figura posta sotto la terza per l’ultima del divisore, e sottragga il risultato, se sarà possibile, dall’ultima posizione del detto avanzo e del numero congiunto. Ma se lo sottrarrà dall’unione dell’ultima figura con la seguente, ponga il resto sopra la medesima posizione. E moltiplichi di nuovo la stessa per la prima del divisore, e sottragga il risultato dal numero rimanente, e ponga al di sopra l’avanzo. E così si applichi a procedere unendo sempre gli avanzi con le figure (seguenti) per le posizioni seguenti, e ponendo secondo giudizio le figure sotto le stesse posizioni, e moltiplicando secondo l’ordine prescritto finché si sarà arrivati alla fine del numero.

(V.26 ; G: V.60) Ma poiché spesso succederà che non si potrà sottrarre il numero divisore dall’unione dell’avanzo e della figura antecedente, allora si dovrà scrivere lo zero sotto la stessa figura antecedente e si uniranno essi, cioè all’antecedente o al seguente, e (al)l’altro all’avanzo, la figura antecedente o seguente, e sotto di essa si ponga quella figura che moltiplicata per il numero divisore farà il numero di quelle dette tre figure, e delle due figure antecedenti o seguenti, cioè delle stesse che risulteranno dall’unione della figura dell’avanzo e delle due figure antecedenti o conseguenti. Per cui se le due ultime figure del dividendo faranno un numero minore del divisore, come abbiamo detto prima, l’ultima posizione del numero risultante dovrà cominciare sotto la terza figura dall’ultima; e così potrai dividere qualunque numero per i suddetti numeri primi. E perché le cose dette siano capite meglio, saranno mostrate con i numeri.

Divisione di 18456 per 17

pg.32

(V.27 ; G: V.62) Se qualcuno volesse dividere 18456 per 17, scriva il 17 sotto il 56 di 18456, e prenda 1 17 da 18 che sono le ultime due figure del numero da dividere che è 1, e resta 1; e ponga 1 sotto l’8 dello stesso 18, e ponga l’1 rimanente sopra l’8, come è mostrato nella prima descrizione. E unisca lo stesso 1 con la figura antecedente, cioè con 4, farà 14 ed essendo questo 14 minore del numero divisore, cioè di 17, porrà 0 sotto lo stesso 4, cioè anteposto all’1 sotto l’8 e unirai questo 14 con la figura antecedente, cioè col 5, farà 145: porrà così sotto il detto 5 con giudizio una figura, tale che moltiplicata per 17 faccia circa 145:

Prima descrizione
		1
	1	8	4	5	6
				1	7
		1	0

(V.28 ; G: V.63) infatti che tale giudizio si abbia da un criterio , si veda dal numero divisore, cioè da 17, a quale numero delle decine è più vicino: è infatti più vicino a 20: si divida quindi 145 per 20, che si fa in questo modo: si tralasci la prima figura del 20, cioè lo zero, dello stesso 20 rimarrà 2; e si tralasci ancora la prima figura di 145, cioè 5, resterà 14, che si divida per il detto 2, risulterà 7; e tale deve essere la figura che dovrà porre sotto il 5 o 1 in più, cioè 8 e ciò accade perché 17 è minore di 20: per cui 1 17 di 145 è una parte maggiore di 1 20 [ di 145 ].

Come trovare
145 diviso 17.

(V.29 ; G: V.65) Ponga così 8 sotto il 5 di 145, perché qui è necessario così, e moltiplicherà l’8 per 17 e sottrarrà la moltiplicazione degli stessi da 145 che si fa così: moltiplicherai dunque l’8 per l’ultima figura del 17, cioè per uno, sarà 8, che sottragga da 14, rimarrà 6 che ponga sopra il 4 del 14 e unisca questo 6 con il 5 antecedente, farà 65, da cui sottragga la moltiplicazione di quello stesso 8 per l’altra figura del 17, cioè per 7, questa moltiplicazione fa 56, rimane 9 e tanto rimane da 145, sottratta da lì la moltiplicazione di 8 per 17, come si mostra nella seconda descrizione:

Seconda
			6
		1	4
	1	8	4	5	6
				1	7
		1	0	8

pg.33

(V.30 ; G: V.66) p onga così il 9 sopra il 5 e lo unirà con la figura antecedente, cioè col 6, farà 96 che resta da dividere per 17, e ponga sotto il 6, di nuovo, tale figura che moltiplicata per 17 sarà più vicina a 96 quanto più si potrà. Da cui, per sapere quale sia quella figura, si tralasci 6 da 96 e divida per 2 il rimanente 9, come abbiamo fatto prima con il 14, rimarrà 1 2 4 : perciò si ponga 5, che è più grande di 1 2 4, sotto il 6, cioè nella prima posizione del numero risultante, e moltiplicherà questo 5 per l’1 di 17, cioè per l’ultima figura dello stesso, farà 5, che sottragga da 9 che è posto sopra il 5, rimane 4, che ponga sopra lo stesso 9, e unirà questo 4 con il 6 antecedente, cioè con quello che prima abbiamo unito al 9, farà 46, da cui si deve sottrarre la moltiplicazione dello stesso 5 per 7, cioè 35, resterà 11 che ponga sopra il 17 conservato da parte sotto la linea [ di frazione ] e il numero che ne risulta, cioè 1085, lo ponga davanti ad essa; e così si avrà 11 17 1085 per la divisione richiesta, come è mostrato nell’ultima descrizione.

Ultima descrizione
				6	4
			1	4	9
		1	8	4	5	6
					1	7
			1	0	8	5
	11 17	1	0	8	5

(V.31 ; G: V.68) Di nuovo, se qualcuno volesse dividere lo stesso 18456 per 19, scriva 19 sotto il 56 di 18456. E ponga sotto il 4 di 184 una figura tale che moltiplicata per 19 faccia circa 184, quale sia lo si conosce nello stesso modo che abbiamo detto per il 17, cioè che si tolga 4 da 184, rimane 18 che si divida per 2, risulterà 9; e tale deve essere la figura da porre, cioè 9: per questo ponga 9 sotto 4, cioè sotto la terza posizione, e moltiplicherà 9 per l’1 di 19, farà 9, che sottragga da 18, rimarrà 9, che ponga sopra l’8 e unisca questo 9 con 4, farà 94, dal quale sottragga la moltiplicazione dello stesso 9 per 9 di 19 che fa 81, rimarrà 13: ponga il 13 sopra il 94, cioè 1 sopra 9 e 3 sopra 4, come si mostra nella prima descrizione.

Prima descrizione
		1
		9	3
	1	8	4	5	6
				1	9
			9

(V.32 ; G: V.70) E unirà 13 con la figura antecedente, cioè con 5, sarà 135. E porrà sotto il 5 una figura tale che moltiplicate per 19 faccia circa 135, e sarà 7: perché se se si toglierà il 5 di 135, rimarrà 13 che se sarà diviso per 2 farà un po’ più di 6: quindi ponga il 7 sotto il 5 e moltiplicherai 7 per l’1 del 19, sarà 7, che si sottrarrà da 13, rimane 6, che ponga sopra il 3 di 13 e unirai 6 con 5, farà 65, dal quale si toglierà la moltiplicazione di 7 per 9, cioè 63, rimarrà 2, che porrai sopra il 5, come è mostrato nella seconda descrizione.

Seconda descrizione
		1	6
		9	3	2
	1	8	4	5	6
				1	9
			9	7

(V.33 ; G: V.71) E unirai 2 con la figura antecedente, cioè col 6 che si trova in prima posizione, farà 26, che dividerà per 19, per così dire, sarà 1 e rimarrà 7: porrà 1 in prima posizione del numero risultante, cioè del 6 e ponga il restante 7 sopra la linea del 19, che si dovrà conservare a parte; e porrà il numero risultante, cioè 971, davanti alla linea stessa; e così si avrà per la divisione richiesta 7 19 971, come è mostrato in questa ultima descrizione.

Ultima descrizione
		1	6
		9	3	2
	1	8	4	5	6
				1	9
	7 19		9	7	1

(V.34 ; G: V.72) Mostrata pertanto la questione del dover decidere sulla posizione delle figure, quando dividiamo per 17 e per 19, mostriamo in particolare ora in che modo decidere nel porre le figure, volendo dividere per i restanti numeri primi al di sotto di cento. E questo è il modo, come quando dividiamo per 17 o per 19, prendiamo la metà del numero da dividere, tolta la prima figura, e anche uno in più: questo poiché 17 e 19 sono minori di 20, come abbiamo già detto; così quando divideremo per 23, prenderemo la metà, e anche uno in meno, poiché 23 è maggiore di 20; e così quando divideremo per 29, dovremo prendere la terza [ parte ] e anche uno in più, poiché 29 è minore di 30, al quale è più vicino che ad altre decine. E così quando divideremo per 31, dovremo prendere la terza parte e anche uno in meno. E così nello stesso modo quando divideremo per 37, dovremo prendere la quarta parte e anche uno in più. E quando divideremo per 41 o per 43, dovremo prendere la quarta parte e anche uno in meno. E quando divideremo per 47, dovremo prendere la quinta parte e anche uno in più. E quando per 53, la quinta parte e anche uno in meno; e quando per 59, la sesta e anche uno in più. E quando per 61, la sesta e anche uno in meno. Quando per 67, la settima e anche uno in più. Quando per 71 o per 73, la settima e anche uno in meno. E quando per 79, dobbiamo prendere l’ottava e anche più. E quando per 83, l’ottava e anche uno meno. E quando per 89, dobbiamo prendere la nona, e anche uno in più. E quando divideremo per 97, dobbiamo prendere la decima parte del numero da dividere, tolta una figura, e anche uno in più. Per cui quando qualcuno dividerà un qualsiasi numero per uno qualunque di quelli scritti sopra, e non saprà se debba dare più o meno di quanto abbiamo detto, ponga quella parte che gli si mostra più sopra, e moltiplichi quella stessa parte per il numero del divisore, e se la moltiplicazione fosse maggiore del dividendo, ne dia uno in meno. E se la moltiplicazione sarà minore più di quanto debba, ne dia uno in più; e così potrà dividere qualunque numero per i numeri suddetti. Tuttavia noi spiegheremo ugualmente tutto questo in alcune divisioni.

Spiega come dividere un numero per un numero primo di due cifre approssimando il divisore per eccesso o per difetto.

Divisione di 13976 per 23

(V.35 ; G: V.76) Ugualmente se qualcuno volesse dividere 13976 per 23, ponga il 23 sotto il 76; e poiché il 23 è maggiore di 13, cioè più del numero delle due ultime figure del numero da dividere, devono essere calcolate le tre ultime figure il cui numero è 139. Dal quale deve iniziare l’ultima posizione del numero risultante sotto il 9 stesso; vi si ponga il 6 che si troverà così per mezzo del detto giudizio, visto che dobbiamo lasciare [ da parte ] la prima figura dal 139, cioè il 9, resta 13 che dobbiamo dividere per 2 poiché 23 è più vicino a 20 che a qualsiasi altra decina, risulterà sei e mezzo

^(PdA)

Per 1/2 sono attestate sia le grafie femminili medietas e, meno spesso, dimidia, sia il neutro dimidium, mentre sono rari [come in questo caso] gli esempi di semis, semissis. [PdA,pag.8]

. Dal quale togliamo quel mezzo, dovendo porre di meno poiché 23 è più di 20 e poniamo 6 sotto il 9, come abbiamo detto; e si moltiplichi questo 6 per il 2 di 23, farà 12, che si toglierà dal 13, resta 1 che va posto sopra il 3 e si unisca col 9, farà 19. E si moltiplichi il 6 per il 3 che è nel 23, farà 18, che si sottragga dal 19, resta 1 che va posto sopra il 9 come si vede nella prima descrizione.

Prima descrizione
		1
	1	3	9	7	6
				2	3
			6

pg.34

(V.36 ; G: V.78) E si unisca questo 1 con il 7 che lo precede nei numeri, farà 17; e poiché questo 17 è minore di 23, bisogna porre lo zero sotto quel 7 e bisogna unire il 6 in prima posizione del numero con il 17 stesso , farà 176: dopo di ciò si ponga sotto il detto 6 una figura tale che moltiplicata per 23 faccia quasi 176; e sarà 7 per il suddetto motivo, che è meno della metà di 17: si moltiplichi così questo 7 per il 2 che è nel 23, farà 14 che va sottratto da 17, resta 3, che si ponga sopra il 7 e lo si unisca con il 6 in prima posizione, farà 36, da cui si sottragga la moltiplicazione di 7 per il 3 di 23, resta 15 che si ponga sopra la linea di frazione del 23 conservato a parte, come si descrive in questa ultima descrizione.

Ultima
					3
			1	1	7
		1	3	9	7	6
					2	3
				6	0	7
	15 23		6	0	7

Prova della divisione scritta sopra

(V.37 ; G: V.80) Se poi si volesse verificare la divisione scritta sopra con il resto del nove, si prenda il resto di 13976, che è 8, e si conservi da parte. E ancora si prenda il resto del risultato, cioè di 607, che è 4, e lo moltiplichi per il resto di 23 che è 5, risulterà 20; dal quale prenda il resto, è 2, e lo sommi col 15 che è sopra la linea del 23, farà 17 il cui resto è 8 come quello che abbiamo conservato prima da parte. Per esempio, poiché dal divisore moltiplicato per il risultato si ottiene il numero diviso, allora se moltiplichiamo la prova del divisore per la prova del risultato avremo la prova del numero diviso: ma dal numero diviso per 23 rimase 15, sottratto il quale da 13976 resta 13961, che diviso per 23 dà 607. Quindi dalla moltiplicazione di 23 per 607 si ha 13961. Perciò se si moltiplica il resto di 607 che è 4 per la prova di 23 che è 5, si ha 20 la cui prova, cioè 2, è la prova di 13961, alla quale si somma la prova del 15 messo sopra che è 6, fa 8, cioè la prova di 13976, e questo volli dimostrare.

Verifica con la prova del 9 l’esattezza della divisione

13976-15=607x23

(V.38 ; G: V.82) Infatti le moltiplicazioni, le addizioni, le sottrazioni o le divisioni dei numeri possono essere provati in altro modo con altri resti, cioè con quella del 7 e di tutti i numeri primi esistenti, come per 11 o per 13 e così via. Dimostreremo questa teorianelle pagine seguenti secondo il modo che ci sembrerà conveniente.

Classi dei resti modulo un numero primo

(V.39 ; G: V.83) Ugualmente se si volesse dividere 24059 per 31, si scriva 31 sotto il 2459 e si ponga 7 sotto lo zero: poiché 31 è circa 30 e di più. Per cui se prenderemo 1 3 di 24, sottratta cioè la prima figura da 240, avremo come terza parte 8 che è più di 7. Quindi poniamo, come abbiamo detto, 7 sotto lo zero; e secondo l’ordine scritto sopra si moltiplichi il 7 per il 3 di 31, farà 21 che si sottragga da 24, resta 3, che si ponga sopra il 4 e si moltiplichi lo stesso 7 per l’1 di 31, farà 7 che si sottragga da 30, resta 23; che si ponga sopra il 30 e si tolga

^(PdA)

Per contrastare la pronunzia assimilata nella lingua scritta si usa interporre tra le nasali la lettera p, come avviene nel verbbo damnare > dampnare [PdA,pag.4]

quel 3, se si vuole; o se non si vuole, si tenga in mente come tolto. Ancora si unisca questo 23 col 5, si avrà 235, e si ponga di nuovo, nel modo prescritto, il 7 sotto al 5, cioè meno della terza parte di 23 e la si moltiplichi per 3, sarà 21 che si sottragga da 23, resta 2: si ponga 2 sopra il 3 e si tolga quel 23 e si unisca col 5, farà 25; e sempre si noti le unioni degli antecedenti con i conseguenti, e si moltiplichi il 7 per l’1, sarà 7, che si sottragga da 25, rimarrà rimane 18: lo si ponga sopra il 25 e si cancelli lo stesso 25. Poi si prenda 1 3 di 18 nel modo scritto sopra, farà 6. Poi si ponga il 6 sotto il 9 e sotto l’1 di 31, posti i quali, lo si moltiplicherà per il 3 di 31, farà 18, per il quali si cancelli il 18 posto sopra e si moltiplichi questo 6 per 1, farà 6, che si sottragga da 9, resta 3, che si ponga sopra la linea di frazione di 31 scritta da parte. E così avrai come risultato della divisione richiesta 3 31 776, come è mostrato in questa descrizione.

		2	2
		3	3	18
	2	4	0	5	9
				3	1
			7	7	6
3 31		7	7	6

pg.35

(V.40 ; G: V.86) Voglio mostrare da dove provenga questo modo di dividere: abbiamo posto il 7 sotto la terza posizione del numero da dividere, che abbiamo moltiplicato per il 3 che è nell’ultima posizione del divisore e occupa la seconda posizione, essendo sotto la seconda posizione del numero da dividere; e da questa moltiplicazione ne viene un numero che termina in quarta posizione: e questo perché la terza posizione qualunque posizione moltiplichi, fa la terza posizione da quello che moltiplica, o fa un numero che termina in esso. Infatti la quarta posizione è la terza dalla seconda. E perciò abbiamo sottratto la moltiplicazione di 7 per 3, cioè 21 dal 24 che termina in quarta posizione; e abbiamo posto il 3 sopra questa quarta posizione, cioè sopra il 4 e abbiamo pensato l’unione di 3 con lo 0 che è in terza posizione del numero da dividere, questa unione è 30: e moltiplichiamo di nuovo quel 7 per l’1 che è nella prima posizione del divisore; e poiché in questa moltiplicazione moltiplichiamo la terza posizione per la prima, il che è lo stesso che moltiplicare la prima per la terza. Per lo stesso motivo sottraiamo la moltiplicazione di 7 per 1, cioè 7, da 30 che termina in terza posizione: per questo dalla moltiplicazione della terza posizione per la prima o della prima con la terza, ne viene un numero di terza posizione o terminante in essa: e abbiamo posto 23 sopra il 30 o nella sua posizione, e abbiamo unito il 23 col il 5 che è in seconda posizione e abbiamo avuto 235, che termina in seconda posizione; e abbiamo posto in seconda posizione un altro 7 che moltiplichiamo ancora per il 3 del divisore, cioè la seconda posizione per la seconda, dalla quale moltiplicazione ne viene un numero in terza posizione o terminante in essa, e perciò abbiamo sottratto 21 da 23, terminando entrambi in terza posizione, e abbiamo posto il 2 rimasto sopra il 3, e abbiamo inteso la sua unione con il 5 seguente, unione che è 25 e termina in seconda posizione, da cui abbiamo sottratto la moltiplicazione di 7 per 1, cioè della seconda pozione per la prima, dalla quale moltiplicazione viene un numero in seconda posizione, o terminante in essa, è rimasto 18 nella stessa posizione nella quale è il 25 cioè 1 in terza posizione e 8 nella seconda; e abbiamo unito questo 18 con il 9 in prima posizione, hanno fatto 189, e abbiamo posto 6 in prima posizione dal risultato e lo abbiamo moltiplicato per 3, cioè la prima posizione per la seconda, moltiplicazione dalla quale è risultato il numero terminante nella seconda posizione, questo prodotto è 18, per questo abbiamo cancellato il 18 detto prima, poiché terminava in seconda posizione: e abbiamo moltiplicato questo stesso 6 per 1, che fa 6 nella stessa posizione, che abbiamo sottratto dal 9 che si trova nella stessa posizione, è rimasto 3 che diviso per 31 fa 3 31; e così abbiamo ottenuto 3 31 776: e valuta secondo tutto questo nelle divisioni simili.

Giustifica il metodo di divisione usato nel caso precedente

La regola di un numero a
è una sua decomposizione come prodotto di primi

a = a₁ × a₂ × ... × a_n

che Fibonacci, mancando di un simbolo per la moltiplicazione, scrive come frazione multipla

1 a =

...

a₁

a₂

...

a_n

(V.41 ; G: V.91) In verità se si desidera conoscere la prova della divisione scritta sopra per mezzo del resto di 7, si prenda il resto di 7 di 24059, cioè dell’avanzo dello stesso numero diviso per 7, avanzo che sarà da ricavare così: si dica che da 1 7 di 24 resta 3, [ da 1 7 ] di 30, andando avanti, cioè unendo [ il 3 con lo 0 antecedente ] resta 2; [ da 1 7 ] di 25 resta 4; [ da 1 7 ] di 49 resta 0, che si avrà come resto: nello stesso modo si prenda il resto di 776, che è 6, e si moltiplichi per il resto di 31 che si trova sotto la linea di frazione, cioè per 3, si avrà 18 che si divida per 7, resta 4 che si sommi al 3 che è sopra la linea di frazione del 31, farà 7, che si divida per 7, resta 0, come doveva rimanere come resto.

Dice come trovare il resto modulo 7

24059 =776 x 31 +3

24059 0 6 × 4 + 3 27 0 (mod 7)

Divisione di 780005 per 59

pg.36

(V.42 ; G: V.92) Se invece si volesse dividere 780005 per 59, scritti i numeri, si ponga l’1 sotto l’8; perché se avremo tolto l’8 dal 78 rimarrà 7; che se l’avremo diviso per 6 dato che 59 è quasi 60, sarà 1 e un po’ di più. Per cui dobbiamo porre 1 sotto l’8, come abbiamo detto prima: posto questo lo si moltiplichi per 5, sarà 5, che si sottragga da 7, resta 2, che si ponga sopra il 7 e si moltiplichi quell’1 per 9, e si sottragga la stessa moltiplicazione da 28, rimarrà 19; e cancelli 2 o elimini [ il 2 ] posto sopra il 7, e ponga il detto 19 sopra il 78. E si ponga il 3 sotto lo 0 nel modo prescritto come posizione, e lo si moltiplichi per 5, farà 15, che si sottragga da 19, rimane 4: si cancelli quel 19 e al posto del 9 si ponga il 4 stesso. E si moltiplichi quel 3 per 9, e si sottragga da 40, rimane 13: si cancelli quel 4 e vi si ponga l’1, e sopra lo 0 si ponga 3: dopo ciò bisogna dividere 130 per 59, si deve dare 2 per questa divisione nel modo suddetto e si deve porre questo 2 sotto lo 0 in terza posizione, moltiplicato questo 2 per 59 e sottratto [ il risultato ] da 130, resta 12; e ciò sarebbe lo stesso se si moltiplicasse questo 2 per 5, e si sottraesse da 13 e lo si moltiplicasse per 9, e lo si sottraesse da 30: si cancelli così 13 e si ponga 1 al posto in cui si trovava il 3 di 13, e si ponga 2 sopra lo 0 in terza posizione. Dopo ciò ponga 2 sotto lo 0 in seconda posizione, e lo moltiplichi per 59, e sottragga [ il risultato ] da 120, resta 2 sopra lo 0; e cancelli dalla mente il 120 che era avanzato dalla divisione precedente, e le figure che si dice [ di ] o eliminare sono così come intenderle cancellate o eliminate: dopo di ciò si unisca questo 2 con il 5 che è in prima posizione del numero, fanno 25, ed essendo minori di 59, si ponga 0 sotto il 5 in prima posizione e 25 sopra la linea di frazione del 59 scritta a parte, come è indicato chiaramente in questa descrizione.

	1	4	3	2
	2	9	13	12	2
	7	8	0	0	0	5
					5	9
		1	3	2	2	0
25 59		1	3	2	2	0

(V.43 ; G: V.95) E affinché le cose che sono state dette splendano in maniera più chiara

^(PdA)

Sin dalla tarda antichità si diffonde l’abitudine di rinforzare avverbi, congiunzioni, sostantivi e verbi indeboliti dall’uso servendosi di prefissi, suffissi, locuzioni alternative. Anziché il classico inniteo figura il derivato innitesco (con il suffisso sco, originariamente incoativo). [PdA,pag.3]

, dividiamo un numero qualsiasi per 97: e sia 5917200, posto il 97 sotto entrambi gli zeri, si divida il numero delle tre ultime figure del dividendo, cioè 591, per 97, per la quale divisione viene 6, perché 97 è più vicino a 100 che a qualunque altra decina. Da qui dobbiamo dividere 59, cioè il numero delle due ultime figure, per 10, dalla quale viene quasi 6, e un decimo in meno; ed essendo il 97 minore di 100, dovremo prendere cinque decine e più. Da lì si è vicini al 6: si ponga questo 6 sotto la prima posizione del numero delle stesse tre figure, cioè sotto l’1 che è in quinta posizione di tutto il numero; e si moltiplichi questo 6 per il 9 di 97, farà 54, che si sottragga da 59, cioè dal numero delle due ultime figure, resta 5 che si ponga sopra il 9; e si moltiplichi lo stesso 6 per il 7 di 97, farà 42, che si sottragga da 51, cioè dall’unione del 5 posto sopra con l’1 antecedente, resta 9, che si ponga sopra l’1 e il 5 posto si elimini o si cancelli dalla mente. E il 9 detto prima che è posto sopra l’1 resta dalla divisione di 591 per 97; questo 9 unito alla figura antecedente in posizione, cioè col 7, che è in quarta posizione del numero, fa 97, che si divida per 97, cioè per il divisore, farà 1: si ponga 1 sotto il 7 e lo si moltiplichi perciò per il 9 di 97, farà 9, per il quale si cancelli il 9 che era avanzato da 591, e si moltiplichi lo stesso 1 per 7, farà 7, per il quale levi il 7 con il quale era stato unito il 9; e non rimanendo nulla di questo 7 per congiungerlo con il 2 antecedente a sé, e questo 2 è minore di 97, si ponga 0 sotto questo 2 e si unisca il 2 con 0 a lui antecedente , e farà 20. Ugualmente, essendo 20 minore di 97, si dovrà porre 0 sotto il detto 0 unito al 2, cioè sotto quello che è in seconda posizione del numero: dopo di ciò si unisca questo 20 con lo 0 a lui antecedente , cioè con quello che è in prima posizione, farà 200 che resta da dividere per 97, per questa divisione bisogna porre 2 sotto lo 0 in prima posizione nel modo scritto prima, e lo si moltiplichi per 9, e lo si sottragga da 20 unito più sopra, resta 2 che si ponga sopra lo 0 in seconda posizione; e si intenda l’unione di questo con lo 0 antecedente che è in prima posizione, e risulta 20, dal quale si sottragga la moltiplicazione del medesimo 2 per 7, resterà 6, che si ponga sopra la linea di frazione di 97 scritta a parte; e si avrà per la divisione richiesta 6 97 61002.


	5	9
5	9	1	7	2	0	0
					9	7
		6


5	9	1	7	2	0	0
					9	7
6 97		6	1	0	0	2

pg.37

(V.44 ; G: V.99) Poiché sembra che sia stato detto abbastanza sulla divisione dei numeri per i numeri di due figure che sono senza regola, cioè hasam, adesso invero si mostrino le loro divisioni per quelli che sono composti, cioè con regola; e sebbene dividere per i numeri composti è come dividere tutti i numeri per quelli primi, tuttavia in maniera più leggera e sottile, nelle pagine seguenti se ne mostra la dottrina, cioè come si trovino le loro regole. Cioè i numeri dai quali sono composti, e si pongano sotto un qualche linea di frazione, così che sempre i minori seguano i maggiori verso sinistra, come si insegna sopra in questo stesso capitolo: dopo questo si divida un numero che si dividere per il minore tra i componenti del divisore, cioè per il numero minore o la figura che sia stata messa sotto la linea di frazione; e se avanzerà qualcosa, lo si ponga sopra la stessa figura o numero, e il numero che risulta dalla divisione si divida per il numero antecedente, o la figura nella linea di frazione, e l’avanzo, se ci sarà, si ponga sopra quello stesso numero o figura antecedente. E così si applichi sempre a dividere sempre con metodo i numeri risultanti dalla divisione per i componenti antecedenti, fino ad arrivare alla fine degli stessi; e si devono porre gli avanzi sopra e si abitui a porre il risultato della divisione dell’ultima componente, cioè dell’ultimo numero che sta sotto la linea di frazione, davanti ad essa. E così si avrà la divisione di qualunque numero per qualunque numero fatta per qualunque numero composto di qualsiasi posizione. Infatti prima di chiarire tutto ciò con le dimostrazioni abbiamo giudicato necessario mostrare come trovare le composizioni dei numeri composti e anche di quelli che sono senza regola. Ed essendo già mostrati in una certa tabella messa sopra i numeri di due figure che sono senza regola, si mostrino in modo simile i divisori dei composti di due figure, singolarmente sotto la linea di frazione; mostreremo poi come trovare mediante una regola le composizioni delle altre posizioni.

Algoritmo per eseguire la divisione per un numero composto.

(V.45.Tab3 ; G: V.103)

COMPOSIZIONI DEI NUMERI DI DUE FIGURE CON QUALI FIGURE SI SCRIVONO

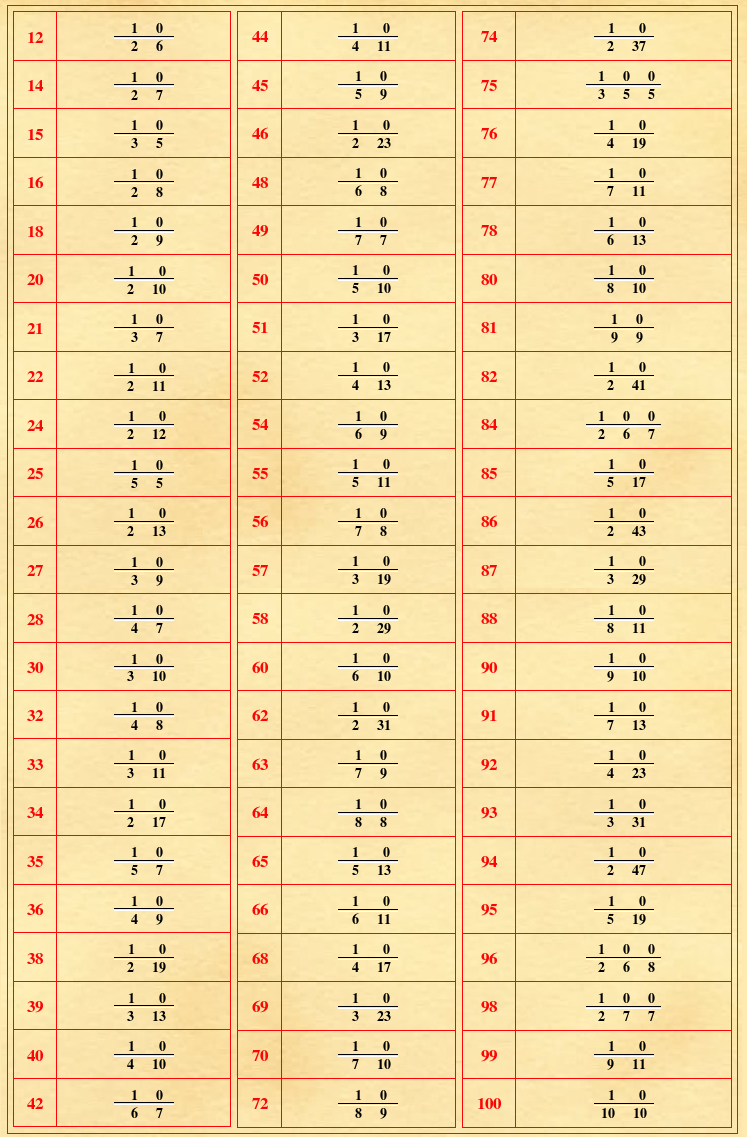
Come fare
le moltiplicazioni a mente

pg.38

Regola generale per trovare le composizioni dei numeri dispari

(V.46 ; G: V.104) Quando inoltre qualcuno abbia appreso per l’uso frequente le regole dei numeri scritti precedentemente nelle tavole, e abbia voluto trovare le regole, cioè le composizioni di qualunque numero [ come prodotto di fattori ] tra gli altri numeri di tre o più figure, o quale fosse un numero primo, cioè senza regola, scriva il numero nella tavola, e dopo averlo scritto veda se il numero sia pari o dispari. Infatti, se sarà pari, si sappia che questo è composto. Se invece è dispari, sarà composto, oppure primo. Infatti i numeri pari sono composti o da pari e dispari, o solo da pari. Pertanto le regole di questi sono da trovare in primo luogo dai numeri pari, come sarà dimostrato a suo luogo. I numeri dispari invece sono composti solo da dispari. Per cui si cerchino le componenti stesse solo per mezzo dei dispari, dai quali prendiamo inizio.

Scomposizione di un numero in fattori primi

(V.47 ; G: V.106) E così quando una figura di prima posizione di un qualunque numero dispari fosse 5, si sappia che è composta dal 5, cioè che si può interamente dividere per 5. Se invece in prima posizione ci fosse un’altra figura dispari che rende dispari tutto il numero, acquisisca il resto per nove di esso, che se sarà zero, allora 1 9 sarà nella sua composizione, e se sarà 3 o 6 allora ci sarà 1 3: se invece il resto non sarà nessuno di questi, lo divida per 7; e se resterà qualcosa divida di nuovo il numero per 11 e se resterà qualcosa lo divida per 13 e sempre vada dividendo per i numeri primi in ordine, secondo come sono scritti nella tavola trascritta sopra, finché si troverà un qualche numero primo, per il quale si possa dividere il numero proposto senza alcun avanzo, o finché si arriverà alla radice del numero stesso: se non potrà essere diviso per nessuno di questi, allora questo numero sarà indicato come primo. Se invece si sarà potuto dividere per qualcuno dei predetti numeri primi senza avanzo, si divida ancora per lo stesso ciò che è risultato dalla divisione e si divida ancora il numero che è risultato dalla divisione per lo stesso numero primo, perché dal medesimo si comincerà a cercare le sue componenti in ordine per i restanti numeri primi fino alla sua radice, se questo non avrà composizione: e si vada avanti facendo sempre così, finché esso abbia avuto tutte le componenti. Avuti questi in modo perfetto, si impari a collocare con grande diligenza i minori prima dei maggiori sotto una linea di frazione. E così si avrà la regola, cioè la composizione di qualunque numero dispari.

Da una procedura per decomporre un numero intero nel prodotto di fattori primi.

(V.48 ; G: V.109) Per esempio: sia dato il numero 805 del quale sia richiesta la regola; poiché la sua prima figura è 5 , nella sua composizione ci sarà di sicuro 1 5. Perciò si divida quel numero per 5, farà 161, il cui resto [ per 9 ], che è 8, mostra come quel 161 non possa essere interamente diviso né per 3, né per 9. Per cui si divida quel numero per 7, farà 23, che è un numero senza regola: metta le componenti trovate , cioè 5 e 7 e 23 sotto una qualche linea di frazione, e si avrà

, per la composizione di 805, cioè cinque per sette di uno di una ventitreesima parte che è un ottocentocinquesimo: perciò svolta la moltiplicazione di cinque per sette, cioè 35, per 23 , si sale fino a 805.

La regola di 805

805=5×7×23
1 805 =

(V.49 ; G: V.111) Ancora, se si chiedesse di trovare la regola di 957, lo si divida per 3, poiché 3 è il resto di questo numero [ per 9 ], farà 319, che non è di nuovo divisibile per 3, poiché il suo resto è 4, e se lo si dividerà per 7, avanzerà e 4; e così lo si divida per 11 e la sua undicesima parte è 29, che è un numero primo: e così collocata la regola trovata sotto la linea di frazione, si avrà per le composizioni di 957

, come qui è mostrato.

La regola di 957

957=3×11×29

1 957 =

Come trovare la regola di 951

pg.39

(V.50 ; G: V.112) In verità, se si volesse trovare la regola di 951, lo si divida per 3; poiché il resto di questo [ per 9 ] è 6, risulterà 317, per cui è impossibile trovare un’altra regola, perché non si può dividere interamente per 7, né per 11, né per 13, né per 17. E non si deve cercare oltre la regola di esso; perché se fosse diviso per 19 risulterebbe dalla divisione un numero più piccolo di 19: quindi la regola di 951 è

317 .

Ancora, se volessimo avere quella di 873, essendo 0 il resto [ per 9 ] di questo numero, lo si divida per 9, risulterà 97, il quale numero 97 è indicato come primo nella tavola più sopra. Questa regola trovata, se sarà collocata sotto la linea di frazione, sarà 1 9 di 1 97.

La regola di 951

951=3×317

19² = 361 > 317
quindi 19 non può
essere fattore di 317.

873=9x97

La ricerca della regola di 1469

(V.51 ; G: V.113) E allora se si volesse avere la regola di 1469, avuto il resto [ per 9 ] di questo numero, che è 2, la regola mostra che esso manca del tre e del 9. Dunque se lo si dividerà per 7, avanzerà 6, se per 11, rimane similmente 6; e se lo si dividerà per 13, risulterà 113, per il quale non occorre più cercare per qualcuno dei numeri primi seguenti o per lo stesso 13; essendo più grande della sua radice [ quadrata ]; quindi si riconosce tra i numeri primi. E quindi la regola di 1469 è, come qui si mostra,

113 .

1469=13×113

La ricerca della regola di 2543

(V.52 ; G: V.114) Ancora, se si volesse avere la regola di 2543, trovato il resto [ per 9 ] di tale numero, che è 5, questo resto dimostra che esso non può avere nella sua regola né 3 né 9. In verità diviso per 7 resta 2. E per 11, resta 2, e per 13, avanza 8. E così si troverà che non si può dividere né per 17, o per 19, o per 29, o per 31, né per 37 o per 41, e neanche per 47 o per 53, e non si deve cercare oltre il 53: poiché 53 è maggiore della sua radice. E se fosse possibile che 2543 potesse avere nella sua composizione un qualche numero primo maggiore di 53, di conseguenza questo numero più grande, viene moltiplicato per un qualche altro [ numero primo ], dovrebbe dare lo stesso 2543, che dovrebbe essere minore di 53, cosa che è impossibile: poiché, cercando la regola dello stesso fino a 53, non l’abbiamo trovato, quindi è un numero senza regola.

2543 è primo

(V.53 ; G: V.116) Ancora, se si volesse trovare [ la regola di ] 624481, si capirà dalle dette disposizioni che questo numero non può avere [ nella regola ] né 3, né 9, né 7: si divida dunque per 11 la cui parte, cioè l’undicesima, è 56771, che ancora si divida per 11, affinché si sappia se si avrà di nuovo 1 11: infatti non occorre che si divida per quei numeri che sono minori di 11, cioè per 9 e per 7 e per 3; per la ragione che non sono stati trovati in 624482. Neanche in questo, cioè in 56771, potranno essere in qualche modo reperiti, essendo della sua stessa composizione. Ma da questa divisione, cioè per 11, risulterà 5161, diviso il quale di nuovo per 11, resta 2. Per questo è impossibile avere di nuovo 1 11: dopo ciò bisogna vedere se si avrà 1 13, cioè lo si divida per 13, da questa divisione risulta 397, nel quale non si potrà trovare né 1 3, né 1 17, o 1 19. Per questo si capisce che il 397 è hasam [ primo ]; poiché tra 19 e la radice di questo numero, non c’è alcun numero primo, cioè senza regola, né si dovrà cercare oltre la sua radice, come abbiamo detto prima: quindi la regola di 624481, come qui si mostra, è 1

0 11

397

624481=11×11×13×397

624481
11
56771
11
5161
13
397
prova 4
1 0 0 0 11 11 13 397

Prova della regola scritta sopra

(V.54 ; G: V.118) E allora se si avrà voluto verificare la regola trovata col resto di 7, si prenda il resto di 624481 per 7 che è 4, e lo si conservi da parte; e si ricavi il resto del primo 11 posto sotto la linea di frazione, che è 4; e lo si moltiplichi per 4, cioè per il resto dell’altro 11, farà 16, che si divida per 7, resta 2, che si moltiplichi per 6, cioè per il resto di 13, sarà 12, dal quale si tolga 7, rimane 5, che si moltiplichi per 5, cioè per il resto di 397, farà 25, che si divida per 7, rimane 4, come è stato serbato per il resto.

Controlla la
scomposizione di

624481=11×11×13×397
modulo 7

Sulla regola dei numeri pari da trovare in modo universale

pg.40

(V.55 ; G: V.119) Se poi qualcuno volesse trovare la regola di un qualche numero pari, prenda in modo simile il suo resto per 9, che se sarà 0, avrà 1 9. E se sarà 3 o 6 avrà 1 6 nella sua composizione, se invece il resto non sarà nessuno di questi, veda quale sarà il resto dividendo per 8 il numero delle due figure che sono in prima e seconda posizione: se questo sarà 0, e la figura in terza posizione sarà pari, o 2 o 4 o 6 0 8, o 0, sappia che tutto il numero in qualunque posizione può essere diviso per 8. Se invece questa terza figura sarà dispari, come 1 o 3 o 5 o 7 o 9, lo stesso numero avrà 1 4 nella sua composizione. Se poi quell’avanzo [ dividendo per 8 ] sarà 4, e la figura in terza posizione sarà dispari, tutto il numero si dividerà in modo simile per 8. E se [ il numero in terza posizione ] sarà pari avrà solo 1 4 nella sua composizione. Se invece quell’avanzo [ dividendo per 8 ] sarà 2, o 6, il numero si dividerà, fra tutti i numeri pari, solo per 2.

a=2a₀ + a₁×10 + a₂×10² + ...

per n>2
10ⁿ = 8 × 5³ × 10^n-3

levando i multipli di 8 resta:
2a₀ + a₁×10 + a₂×10²

(V.56 ; G: V.121) E in base a ciò prenda le composizioni pari dei numeri pari, fino ad avere la regola dello stesso , o incontri qualche numero dispari: del quale dispari si impegni a trovare la regola secondo il sovrascritto ordine dei numeri dispari. In verità se in prima posizione di qualunque numero pari ci sarà 0, lo tolga, e al suo posto metta 1/10 nella composizione di quel numero. E se sarà rimasto un altro 0 all’inizio del numero, lo si tolga ancora dal numero , e si avrà ancora 1/10 nella composizione dello stesso numero. E così sempre si deve intendere, finché lo 0 sarà all’inizio del numero. E affinché si capiscano più chiaramente le cose che sono state dette sulla ricerca delle regole dei numeri pari, queste siano mostrate con spiegazioni numeriche.

Come trovare la regola di 126

(V.57 ; G: V.123) Così se si chiedesse la regola del 126, poiché il suo resto [ per 9 ] è 0, mostra che la sua nona parte è intera: per cui si divida 126 per 9, farà 14, la cui regola [ è mostrata ] più sopra, nella tavola delle regole dei numeri composti di due figure di seconda posizione, si dimostra essere senz’altro

: da cui per la regola di 126 si avrà

, come qui si mostra. Parimenti, se si cerca la regola di 156, il suo resto [ per 9 ], che è 3, indica che può essere diviso per 6, e diviso per 6, ne risulta 26, la cui regola è

13 ; e così si avrà la regola di 156, come qui è annotato,

13 .

126 = 2×7×9

(V.58 ; G: V.125) Se invece si volesse trovare quella di 2112, poiché il suo resto [ per 9 ], che è 6, mostra che esso può essere diviso per 6. Si divida dunque 2112 per 6, farà 352, il cui resto acquisito che è 1, mostra che non si può dividere né per 6 né per 9: per cui di deve dividere 52, cioè il numero di due figure, per 8, dalla cui divisione resta 4: da questo resto, e dalla figura in terza posizione nel numero, cioè il 3 davanti, si mostra che si può dividere 352 per 8; e si divida per 8, farà 44, la cui regola è

: per cui si ha come regola di 2112, come qui si mostra,

11 . E allora, poiché

che sono contenuti nella stessa linea di frazione sono la regola di 24, che si scopre avere nella tavola dei numeri composti una regola migliore, cioè

poiché la figura in essa è maggiore che in

, perché 8 è maggiore di 6, per questo bisogna sempre assumere le regole estreme dei numeri, regole che sono composte da numeri che vanno da due fino a 10, come sarà mostrato nelle pagine seguenti. Per cui la regola trovata deve essere sistemata, cioè da

11 in

11 .

2112 = 4×6×8×11 =

= 3×8×8×11

3
	2	1	1	2
6
3
3			5	2
8
4				4
1 0 0 0 4 6 8 11

Come trovare la regola di 4664

pg.41

(V.59 ; G: V.127) Invece se si volesse trovare la regola di 4664 , il suo resto [ per 9 ], che è 2, mostra che non può avere né 1 6 né 1 9. E poiché dal numero di due figure che è all’inizio del numero, cioè 64 diviso per 8, resta 0; e le figura che si trova in terza posizione, cioè 6, è pari; per cui si saprà che 4664 ha 1 8 : per cui se lo si dividerà per 8, dalla divisione si avrà proprio 583; la cui regola, se la si cercherà con la suddetta dottrina dei numeri dispari si troverà che essa è

53 , da cui come regola di 4664 si avrà

53 .

4664 = 8×11×53

6			2
	4	6	6	4
8
3
5			8	3
1				1
5				3

1 0 0 8 11 53

(V.60 ; G: V.128) Se poi si vorrà trovare la regola di 13652, il suo resto [ per 9 ], che è 8, indica che esso manca di 1 6 e di 1 9. In verità se il numero di due figure che si trova al suo inizio sarà diviso per 8, rimarrà 4. Per cui, essendo pari la figura in terza posizione, cioè 6, è pari, questo indica che nella regola c’è 1 4: perciò 13652 sarà diviso per 4, farà 3413; che essendo senza regola si prenderà come regola di 13652, come qui è mostrato, 1

3413 .

13652 = 4×3413

Come trovare la regola di 15560

(V.61 ; G: V.129) E così, se si volesse trovare la regola di 15560, essendo lo 0 in prima posizione, lo si tolga, e per esso si abbia 1 10 nella regola del numero scritto sopra: in seguito ci si applichi a trovare la regola del numero rimanente, cioè quella di 1556, il cui resto [ per 9 ], che è 8, mostra che essa manca di 1 6 e di 1 9. E poiché dal numero delle due figure che stanno all’inizio, cioè 56, diviso per 8, resta 0 ; e poiché la figura in terza posizione, cioè 5, è dispari, si mostra che nei numeri pari non si può avere nessuna regola maggiore di 4. Infine 1556 diviso per 4 fa 389, che si trova ad essere senza regola per quanto si è mostrato prima. Per cui si avrà come regola di 15560, come qui si mostra,

389 .

15560=4×10×389

3		3
1	5	5	6	0
4
3		8	9	0

1 0 0 4 10 389

(V.62 ; G: V.131) Parimenti se si volesse trovare la regola di 32600, poiché nella prima posizione di questo c’è 0, nella sua regola deve avere 1 10 per questo 0 e tolto questo 0 dal numero, resta 3260. Nella cui prima posizione c’è ancora 0, per il quale si deve avere di nuovo 1 10. E tolto anche questo dal numero resta 326, il cui resto [ per 9 ], che è 2, non permette di poter avere 1 6 o 1 9 nella sua composizione. In verità 26, che è il numero di due figure all’inizio di 326, se si divide per 8, resta 2: per questo capiamo che non si può dividere per un qualsiasi numero pari all’infuori che per due. Quindi da questo 326 diviso per 2 risulta 163, e non avendo questo regola [ essendo primo ] si avrà per quella di 3200 1

163 .

32600=2×10×10×163

(V.63 ; G: V.133) E se si volesse trovare quella di 7546000, tolti dal numero tre zeri, e avuto per essi

0 10

10 , resta 7546. Il cui resto [ per 9 ] che è 4 non permette che possa avere 1 6 o 1 9 nella sua composizione. Infatti se 46, che è all’inizio di 7546. Sarà diviso per 8, resta 6, per cui si saprà che non può avere nessun altro numero pari, al di fuori di 2 dopo di se: cioè se questo 7546 sarà diviso per 2, risulterà 3773, la cui regola, se si farà in modo di trovarla secondo la dottrina dei numeri dispari , si troverà essere 1

0 7

11 . Se questa regola sarà messa bene nella linea di frazione con quella trovata più sopra, cioè con

0 10

10 , si avrà come regola di 7546000 1

0 2

11 .

7546000 =
=2×7×7×7×10×10×10×11

Divisione di 749 per 75

(V.64 ; G: V.134) Se, acquisito il modo di trovare le regole dei numeri, qualcuno volesse dividere 749 per 75, trovata la regola di 75, che è 1

0 3

5 , si divida 749 per 3, farà 249, e resta 2; questo 2 si ponga sora il 3 della linea di frazione conservata da parte, e si divida 249 per 5, per quello cioè che antecede il 3 in frazione, farà 49 e resta 4; questo 4 si ponga sopra lo stesso 5, e si divida di nuovo 49 per 5, per quello che si trova alla fine della linea di frazione, fa 9 e rimane 4; questo 4 si ponga sopra lo stesso 5, e 9 si ponga davanti alla medesima linea di frazione; e così di avrà dalla divisione richiesta , come qui si mostra, 2

4 3

5 9

75 = 3×5×5

749 3 = 249+ 2 3

1 5×(249+ 2 3) = 49+ 4 5+ 2 5×3

1 5 × (49 + 4 5 + 2 5×3) =

= 9 + 4 5 + 4 5×5 + 2 5×5×3 =

= 2

4 3

5 9

Divisione di 67898 per 1760

pg.42

(V.65 ; G: V.135) Ma se si volesse dividere 67898 per 1760, trovata la regola di 1760, che è 1

0 2

11 , si divida 67898 per 2, risulterà 33949, e resta 0; si ponga questo 0 sopra il 2 e si divida 33949 per 8, farà 4243 e resta 5, si ponga questo 5 sopra l’8 della linea di frazione, e si divida 4243 per 10, risulterà 424 e resta 3, cioè come se si togliesse la figura in prima posizione di 4243; si divida questo 424 per 11, farà 38 e resta 6, si ponga questo 6 sopra l’11 della linea di frazione e si ponga il 38 davanti alla linea di frazione; e così si otterrà, per la divisione richiesta 0

6 2

11 38 .

1760 = 2 × 8 × 10 × 11

Prova della divisione sovrascritta

(V.66 ; G: V.136) Se si volesse verificare tale divisione col resto del 13, si divida il 67898 scritto sopra per 13, resta 12, che si abbia come resto. Dopo ciò, si divida il 38 davanti alla linea di frazione posta per 13, resta 12 che si moltiplichi per l’11 della linea di frazione, e in più si addizioni il 6, che è sopra l’11, farà 138; che si divida per 13, rimane 8; che si moltiplichi per il 10 della linea di frazione e in più si aggiunga il 3 che è sopra il 10, farà 83; che si divida per 13, resta 5; che si moltiplichi per l’8 della linea di frazione e in più ci aggiunga il 5 che è sopra l’8, risulta 45 che si divida per 13, resta 6 che si moltiplichi per il 2 della linea di frazione, risulterà 12, come è stato conservato più sopra come resto. E bisogna stare attenti che nessuno si abitui a fare la prova di qualche divisione per qualche resto di qualche numero che sta sotto la linea di frazione della divisione, perché facilmente potrebbe essere ingannato a causa sua; perciò in questa divisione si proibisce di fare la prova per 11, perché dal resto che rimarrebbe da 38 o da qualsiasi altro numero moltiplicato per l’11, che è sotto la linea di frazione, e diviso per l’11 della prova, non avanzerebbe nulla: quindi non si potrebbe sapere con la prova dell’11, se questo 38 non fosse corretto.

b₁ × ...a₃ a₂ a₁ ...b₃ b₂ b₁ a =
...a₃ a₂ ...b₃ b₂ (a× b₁+a₁)

Dovendo verificare se

a=bq+r dati a e b

la prova con un divisore di b non coinvolgerebbe q e quindi sarebbe non significativa

(V.67 ; G: V.138) E si sappia che per dividere i numeri c’è un’altra dottrina, cioè quando il numero da dividere ha una parte in comune con il divisore, cioè il fatto che il numero dividendo si può dividersi integralmente per qualche numero, o numeri che sono secondo la regola del divisore. Allora dapprima si divida il numero per il numero della composizione che il dividendo stesso avrà nella linea di frazione del divisore, sia che sia il maggiore nella linea di frazione, sia che sia il minore: infatti quando si sarà diviso questo per quello, dalla divisione non ci sarà alcun resto. E affinché ciò si comprenda più chiaramente, questo si mostri con i numeri nel seguito.

Divisione di 81540 per 8190

(V.68 ; G: V.139) Così, se si volesse dividere 81540 per 8190, si trovi la regola del divisore, che è 1

0 7

13 ; e dal momento che nella regola di 81540 c’è, 1 10 per lo 0 che è nella sua primo posizione, sebbene 10 non sia all’inizio della linea di frazione, tuttavia 81540 è da dividere prima per 10, cioè si tolga 0 da tale numero, resterà 8154 che resta da dividere, una volta sottratto 1 10 dalla linea di frazione, per 1

0 7

13 . Ugualmente si divida 8154 per 9, poiché 0 è il loro resto per 9 di entrambi. Per cui lo si divida per il 9 della linea di frazione, risulterà 906, che resta da dividere per 1

0 7

13 : ma 906, diviso per 7, dà come risultato 129 e resta 3; si ponga questo 3 sopra il 7. E si divida 129 per 13, risulta 9 e resta 12, che si ponga sopra il 13, e si ponga il 9 risultato davanti alla linea di frazione, e si avrà per la divisione richiesta 3

12 7

13 9.

Semplifica 81540 8190
dividendo numeratore e denominatore per 90

Esegue la divisione

906 7×13

pg.43

(V.69 ; G: V.141) Dunque se si vorrà verificare la divisione scritta sopra, si dovranno porre il 10 e il 9 che sono stati sottratti dalla linea di frazione, sotto la stessa linea di frazione dopo il 7, e sopra di essa bisogna porre due zeri, come si vede in questa linea di frazione

12 10

13 : poi si potrà fare la prova della divisione secondo il prescritto ordine del fare la prova. O altrimenti si consideri 906 come numero diviso e 1

0 7

13 come divisore, e in base a ciò ci si applichi a fare la prova nel modo detto sopra. Infatti potrebbe sembrare che sia stato detto abbastanza sulle divisioni dei numeri per i numeri composti, se non ci fossero nelle loro composizioni numeri di tre o più figure. Ma affinché in questo opuscolo sia contenuta la completa dottrina del dividere, nelle pagine seguenti si mostri come dividere i numeri per quelli che sono di tre o più figure.

Divisione dei numeri per numeri primi di terza posizione.

(V.70 ; G: V.143) Quando poi qualcuno avrà voluto dividere un qualunque numero di qualunque posizione per un qualunque numero di tre figure, cioè di terza posizione, ponga la simile posizione di quel numero di tre figure sotto la simile posizione del dividendo e veda prima se il numero formato dalle ultime tre figure del dividendo sia maggiore del divisore: se infatti sarà maggiore o uguale, si dovrà iniziare l’ultima posizione del numero risultante sotto la terza figura dall’ultima; e se sarà minore bisognerà iniziare sotto quella precedente, cioè sotto la quarta figura dall’ultima. E conviene che la figura posta sotto una qualunque delle figure suddette sia tale che, moltiplicata per il numero divisore, cioè per quello per il quale viene diviso il numero maggiore, realizzi il numero formato dalle ultime 3 o 4 figure, o quasi così, affinché non rimanga da ciò il numero del divisore o qualcosa in più. E allora la si moltiplichi per l’ultima figura del numero divisore. E se si potrà, si sottragga la moltiplicazione dal numero dell’ultima figura. E se no, lo si sottragga dal numero delle ultime due figure, e il resto si ponga sopra la stessa posizione dal quale sarà avanzato. E moltiplichi di nuovo la stessa figura posta per l’antecedente all’ultima del numero divisore, cioè per quella che è nella seconda posizione dello stesso; e sottragga il totale risultante dall’avanzo detto sopra unito con la figura antecedente nel numero maggiore: e se ci fosse un avanzo, ponga la sua prima posizione sopra la medesima figura antecedente, e i restanti poi dopo di esse cioè cancellando, o eliminando l’altro avanzo posto prima. E ancora moltiplichi la stessa figura posta per la figura di prima posizione di questo numero divisore e sottragga il totale della moltiplicazione dall’unione del secondo avanzo con la figura precedente del numero maggiore; e ponga la prima posizione del suo avanzo sopra la figura antecedente stessa; e cancellando poi i restanti dopo di esso, cioè eliminando l’altro avanzo in base a quanto detto. Dopo di ciò, si applichi a porre un’altra figura sotto l’altra figura antecedente del numero maggiore, cioè davanti alla prima figura posta, che moltiplicata per il suddetto numero divisore, faccia l’unione del terzo avanzo e della figura antecedente o quasi, con la quale proceda moltiplicando in ordine per le figure del numero divisore, come si è insegnato per la figura posta per prima, sovrapponendo sempre gli avanzi in successione; e poi si applichi a operare similmente per le restanti figure procedendo fino alla fine. Ma se da qualcuno degli avanzi suddetti e dalla figura antecedente si produrrà un numero minore del divisore, allora ponga uno zero sotto la figura antecedente stessa; e lo unirà alla medesima figura antecedente, e all’avanzo l’altra figura antecedente sotto la quale, davanti al suddetto zero, bisognerà porre ancora una figura: e se di nuovo il numero dell’unione dell’avanzo e delle due figure antecedenti, sarà minore del divisore, si dovrà di nuovo porre davanti al suddetto zero un altro 0, e unirà al suddetto avanzo e alle suddette due figure l’altra figura ad esse antecedente sotto la quale ponga tale figura che moltiplicata per il numero divisore dia come risultato quasi il numero formato dall’unione del resto e delle tre figure ad esso antecedenti; e si avranno le divisioni di qualsiasi tipo simile, e affinché le cose che sono state dette siano spiegate più chiaramente, le mostreremo con i numeri.

Spiega come dividere un numero qualsiasi per un numero di tre cifre

pg.44

(V.71 ; G: V.151) Se si volesse così dividere 1349 per 257 , si scriva il 257 sotto il 349 di 1349. E poiché il numero delle ultime tre figure del numero da dividere, cioè 134, è minore di 257, cioè del numero divisore, allora si dovrà porre la figure del numero risultante sotto la [ successiva ] quarta figura dello stesso numero dividendo, che occupa la prima posizione, cioè sotto il 9; e tale che, moltiplicata per 257, farà quasi 1349, questa [ figura ] sarà 5; posta questa sotto il 9, la si moltiplichi per l’ultima figura del numero divisore, cioè per il 2, farà 10 che si sottragga da 13, cioè dal numero formato dalle ultime due figure del numero da dividere; poiché non può essere sottratto dal numero dell’ultima figura, resta 3, che deve essere unito con il 4 antecedente, farà 34; da cui si sottragga la moltiplicazione del 5 posto per il 5 del numero divisore, resta 9, che si ponga sopra il 4 e si moltiplichi il medesimo 5 posto per 7, farà 35, che si sottragga da 99, cioè dall’unione del 9 in prima posizione del dividendo [ con il 9 detto prima ], resta 64; che si ponga sopra la linea di frazione col 257 messo a parte. E si ponga il 5 che risulta davanti alla stessa linea di frazione e si avrà per la divisione richiesta 64 257 5

3			9
	1	3	4	9
		2	5	7
5
64 257 5

Divisione di 30749 per 307

(V.72 ; G: V.154) Invece se si volesse dividere 30749 per 307, si scriva il 307 sotto il 749; e poiché 307, che è il numero formato dalle ultime tre figure del numero da dividere, è uguale al numero che divide, bisogna porre l’1 sotto la prima posizione del numero formato dalle predette tre figure, cioè sotto il 7 che è in terza posizione del dividendo; e si moltiplichi tale 1 per il 3 del divisore, farà 3, per il quale si tolga il 3 che è nell’ultima posizione del dividendo; e si moltiplichi di nuovo tale 1 per lo 0 del divisore, farà 0; per il quale si tolga lo stesso 0 che è nel numero da dividere; e di nuovo si moltiplichi quell’ 1 per 7, farà 7, per il quale si tolga lo stesso 7 che è nel numero da dividere. Infatti la terza posizione, qualunque posizione moltiplichi, fa la terza posizione da quello che moltiplica. Dunque quando moltiplica il terzo fa la quinta posizione; e quando moltiplica il secondo, fa la quarta; e quando moltiplica la prima, fa la terza. E poiché 4, che precede il 7 nel dividendo, è minore di 307, cioè del divisore, bisogna porre uno 0 sotto il 4 stesso; e ancora, poiché il 49 del medesimo dividendo è minore dello stesso 307, si ponga 0 sotto il 9, cioè nella prima posizione del numero risultante; e si ponga il suddetto 49 sopra la linea di frazione del 307 conservato da parte, e si ponga il 100 che risulta davanti alla linea di frazione; e si avrà per la divisione richiesta 49 307 100.

4
3	0	7	4	9
		3	0	7
1			0	0
49 307 100

pg.45

(V.73 ; G: V.157) Ugualmente se si proporrà di dividere 574930 per 563, posto il 563 sotto il 930, si ponga in base alle suddette disposizioni l’1 sotto il 4, cioè in quarta posizione, e lo si moltiplichi per il 5 del numero da dividere, fa 5, per il quale si tolga il 5 che è nell’ultimo posizione del dividendo: poiché quando la quarta posizione moltiplica la terza, fa la sesta posizione, cioè la quarta da quella che moltiplica; e si moltiplichi lo stesso 1 per il 6 del divisore, fa 6 che si sottragga da 7, resta 1, che si ponga sopra lo stesso 7: infatti quando la quarta posizione moltiplica la seconda, fa la quinta posizione; e di nuovo si moltiplichi l’1 per il 3 del divisore, farà 3; che si sottragga da 4, cioè da 14, per l’1 che è rimasto sopra il 7: infatti quando la quarta posizione moltiplica la prima, determina la quarta posizione o una posizione terminante in essa. E perciò il predetto 3 deve essere sottratto da 4, che è in quarta posizione, cioè da 14 che termina in esso, resterà 11, cioè un 1 sopra la quinta posizione e l’altro sopra la quarta; col quale si unisca 11 con il 9, farà 119, che essendo il quale minore di 563, cioè del divisore, va posto uno 0 sotto il 9 stesso; e si unisca il 3 che è nella seconda posizione del dividendo con il 119, farà 1193. Per questo ponga in seconda posizione, secondo giudizio, una figura tale che moltiplicata per 563 faccia quasi 1193, questa figura sarà 2, che si moltiplichi per il 5 del divisore, farà 10, che si sottragga dall’11 scritto sopra, resta 1; per il quale si tolga lo stesso 1 che era stato posto sopra il 4, e si cancelli l’altro 1 che è sopra il 7, e si moltiplichi il 2 per il 6 del divisore, fa 12; che si sottragga da 19, resta 7 che si ponga sopra il 9 e si cancelli l’1 che è sopra il 4; e si moltiplichi il 2 per il 3 del divisore, fa 6; che si sottragga da 73, resta 67 : si cancelli il 7 che era sopra il 9 e si ponga il 67 sopra il 93, come si ha nella descrizione. E si unisca il 67 stesso con lo 0, sarà 670; per queste dette disposizioni, si ponga l’1 sotto lo 0, e lo si moltiplichi per il 5 del divisore, fa 5, che si sottragga da 6, resta 1: si cancelli il 6 stesso e si ponga lì 1; e si moltiplichi 1 per 6, fa 6; che si sottragga da 7, resta 1: si cancelli il 7 e si ponga lì l’1 stesso; e si moltiplichi l’1 per il 3 del divisore, fa 3, che si sottragga da 110, resta 107, che si ponga sopra la linea di frazione di 563 e davanti ad essa si ponga il risultante 1021, come è descritto in questa figura.

1
		1	6	1
1		1	7	7
5	7	4	9	3	0
			5	6	3
1			0	2	1
107 563 1021

Verifica della suddetta divisione

(V.74 ; G: V.162) Se si avrà vorrà verificare questa divisione con la prova dell’11, si divida 574930 per 11, resta 4, che si conservi come resto; e si divida similmente il risultato 1021 per 11, resta 9, che si moltiplichi per il 2 che resta da 563 diviso per 11, farà 18; ad esso si addizioni il resto del numero che rimane sopra la linea di frazione, cioè di 107, il quale resto è 8: poiché da 107 diviso per 11, resta 8; e cosi si avrà 26, diviso il quale per 11 resta 4, com’è necessario che rimanga come resto.

574930 = 1021×563+107

(V.75 ; G: V.163) E così tramandiamo questo insegnamento per sapere come porre le figure dei risultati, quando numeri di tre o più figure sono divisi per numeri di tre figure, perché si consideri se il divisore sarà stato abbastanza vicino ad un qualche numero delle centinaia, o un po’ di più, o un po’ di meno - e si guardi di fronte a quali figure sia da porre la figura del numero risultante, e tra quelle figure si levino le due che sono in prima e in seconda posizione di esse. Poi si divida il numero che resta per il numero delle centinaia a cui il divisore sarà il più vicino; e dovrà essere posta la figura di quanto risulterà dalla divisione, o un poco più, se il divisore sarà inferiore al suddetto numero delle centinaia, o un poco meno se il divisore sarà maggiore dello stesso numero delle centinaia. Per esempio, vogliamo dividere 1247 per 421, leviamo 47 e dividiamo il 12 che resta per 4; poiché 421 è più vicino a 400 che ad un altro numero delle centinaia, ne viene 3, ma si dovrà dare un po’ di meno, perché 421 è maggiore di 400: e se fosse inferiore, come 379, bisognerebbe dare un’unità in più; e così s’intenda per il resto. E se il divisore non sarà vicino ad alcun centinaio, e intermedio come 150, o duecentocinquanta, e come gli altri simili: allora, tolte le due figure suddette, si raddoppi il numero restante e si divida la somma raddoppiata per il doppio delle centinaia e per la metà e si avrà la scelta della figura da porre. Per esempio: vogliamo dividere 2137 per 563, dividiamo 21 per 1 2 5 , cioè il doppio di 21, cioè 42, per il doppio di 1 2 5 , cioè per 11, farà 3 e un po’ di più; e allo stesso modo si decida in simili casi.

Spiega come dividere
un numero di tre cifre
per un numero di tre cifre

pg.46

(V.76 ; G: V.166) Ugualmente se si sarà voluto dividere 5950000 per 743, scritti i numeri, si ponga l’8 sotto lo 0 in quarta posizione in base alle suddette disposizioni, cioè poiché, tolto il 50 di 5950, resta 59; il cui doppio se si divida per il doppio di 1 2 7 , a causa del divisore che è quasi 750, dalla divisione risulterà quasi 8; e si moltiplichi l’8 per il 7 del divisore, farà 56, che si sottragga da 59, resta 3; che si ponga sopra il 9. E 8 per 4, fa 32, che si sottragga da 35, resta 3; che si ponga sopra il 5, e si cancelli il 3 stesso che era stato posto sopra il 9. E 8 per 3 del divisore fa 24, che si sottragga da 30, resta 6; che si ponga sopra lo 0, e si cancelli il 3 che era sopra il 5; e così moltiplicata sempre la figura posta, ad una ad una per le figure del numero divisore, cioè iniziando dall’ultima fino ad arrivare alla prima, è sempre opportuno che la divisione rimanga nella stessa figura; sotto la quale si raccomanda sia posta la figura, come si è mostrato nella prima descrizione di quella divisione. Dopo di ciò si pongano due zeri sotto i due zeri di terza e seconda posizione, poiché entrambi gli zeri, uniti con il 6, fanno un numero inferiore a 743. Per cui si deve prendere il 6 con tre zeri, cioè 6000, e si deve dividerlo per 743, divisione per la quale si deve porre l’8 in prima posizione del numero risultante, cioè sotto lo 0 in prima posizione: per il fatto che, diviso il doppio di 60 per il doppio di 1 2 7, ne viene 8; Moltiplicato tale 8 per 7, e sottratto [ il risultato ] da 60, resta 4; si ponga questo 4 sopra lo 0 in terza posizione, e si elimini il 6 che è sopra lo 0 in quarta posizione, e di nuovo moltiplicato l’8 per il 4 del divisore, e sottratto il risultato da 40, resta 8: infatti così come la moltiplicazione dell’8 scritto sopra per il divisore si muta in ordine, posizione per posizione, così le moltiplicazioni di esso peril dividendo devono mutare di posizione in posizione. Si ponga pertanto l’8 del resto sopra lo 0 in seconda posizione e si cancelli il 4 che era stato posto sopra lo zero di terza posizione; e si moltiplichi l’8 per il 3, fa 24 che si sottragga da 80, resta 56; che si ponga sopra la linea di frazione di 743 e davanti ad essa si ponga 8008; e si otterrà il risultato della suddetta divisione. E benché grazie alle cose che sono state dette sulla divisione si è potuto avere un pieno insegnamento nei numeri da dividere per numeri di quattro o più figure, tuttavia, perché si capisca meglio, si mostrino le suddette divisioni per alcuni numeri di quattro figure.

5	9	5	0	0	0	0
7					4	3
8

5						6
5	9	5	0	0	0	0
7					4	3
8				0	0	8
56 743 8008

Divisione di 17849 per 1973.

(V.77 ; G: V.172) Se per esempio sia proposto di dividere 17849 per 1973, si scriva il divisore sotto il dividendo, cioè il 1973 sotto il 7849 di 17849; e poiché il numero delle ultime quattro figure del numero da dividere, cioè 1784, è minore del divisore, è necessario che la posizione della figura del numero risultante sia sotto la prima posizione del numero da dividere. Per cui si ponga il 9 sotto la prima posizione di entrambi i numeri; poiché il 9 moltiplicato per il divisore, fa quasi il numero da dividere; o poiché il divisore è quasi 20 centinaia, bisogna dividere il 17 per 2 e togliere le tre figure del dividendo, cioè 849: e allora si moltiplichi il 9 stesso per l’1 del divisore e si sottragga [ il risultato ] dal 17, resta 8 che si ponga sopra il 7, e si moltiplichi il 9 per il 9 del divisore e si sottragga [ il risultato ] da 88, resta 7 che si ponga sopra l’8 e si elimini l’8 posto. E di nuovo si moltiplichi il 9 per il 7 del divisore, e si sottragga [ il risultato ] da 74, resta 11, che si ponga sopra il 74, e si moltiplichi 9 per il 3 del numero divisore e si sottragga da 119, resta 92, che si ponga sopra la linea di frazione di 1973, e davanti ad essa si ponga il 9; e si otterrà il numero della divisione proposta.

	1	7	8	4	9
1			9	7	3
9
92 1973 9

Divisione di 1235689 per 4007

pg.47

(V.78 ; G: V.175) Ugualmente se si volesse dividere 1235689 per 4007, una volta scritti i numeri, si ponga il 3 sotto la terza posizione dei numeri, scritti sopra cioè disposti; e si moltiplichi il 3 stesso per il 4, fa12, per il quale si tolga il 12 che è il numero formato dalle ultime due figure del numero da dividere. E si moltiplichi il 3 per lo 0, che è nella terza posizione del divisore, farà 0; che si sottragga dal 3 che è nel numero da dividere, resta lo stesso 3. E ancora si moltiplichi il 3 per lo 0 in seconda posizione del divisore, farà 0. che si sottragga da 35, resta ancora lo stesso 35. E 3 per 7 fa 21, che si sottragga da 356, resta 335 che si ponga sopra 356. Infatti, poiché 3358, che è l’unione del numero rimanente con la figura ad esso antecedente, è inferiore a 4007, si deve porre uno 0 davanti al 3 posto, cioè sotto la seconda posizione dei numeri, e bisogna unire il 3358 con la figura precedente, cioè con il 9, sotto il quale si ponga l’8 nel numero risultante. E si moltiplichi tale 8 per 4 e si sottragga [ il risultato ] dal 33, resta 1, che si ponga sopra il 3 in prima posizione del 33 e si cancelli il 33. E [ si moltiplichi ] l’8 per lo 0 di terza posizione e si sottragga da 15, resta 15. E di nuovo si moltiplichi l’8 per lo 0 di seconda posizione del numero divisore, e si sottragga [ il risultato ]da 158, resta lo stesso 158. E 8 per 7 fa 56, che si sottragga da 1589, resta 1533 che si ponga sopra la linea di frazione di 4007, e davanti ad esso si ponga il 308; e si avrà il risultato della divisione richiesta, come si vede in questa figura.

1					5
3			35	335	8
1	2	3	5	6	8	9
4				0	0	7
3					0	8
1533 4007 308

(V.79 ; G: V.178) Ma se si volesse verificare questa o qualunque altra divisione in un modo diverso che con il resto, si moltiplichi il numero risultante per il divisore e al risultato si addizioni il numero che rimane dalla divisione, cioè quello che si raccomanda di porre sopra la linea di frazione. Così in questa si moltiplichi 308 per 4007 ,e alla moltiplicazione si addizioni 1533 che è sopra la linea di frazione; e se il risultato dell’addizione farà il numero diviso, si sappia che questa divisione sarà corretta.

Termina il quinto capitolo.