pg.1
Inizia il Liber abaci composto da Leonardo figlio di Bonacci Pisano nell’anno 1202


Michele Scoto 		(I.1 ; G: I.1) Mio signore e maestro, sommo filosofo, Michael Scottus mi avete scritto di copiare per voi il libro sul numero che ho scritto tempo fa, per cui, assecondando la vostra richiesta, esaminandolo con accuratezza, l’ho corretto in vostro onore e per renderlo utile a molti altri. Durante la correzione ho aggiunto qualcosa di necessario e tagliato qualcosa di superfluo. In esso ho reso nota l’intera dottrina dei numeri secondo il metodo indiano, metodo che ho scelto come il più efficiente in questa scienza. Dedica a Michele Scoto
(I.2 ; G: I.3) E poiché la scienza aritmetica
(PdA)
Leonardo usa costantemente arismetrica al posto del latino classico arithmetica  [PdA,pag4]
e quella geometrica sono connesse e si sostengono a vicenda, non si può trasmettere una piena dottrina del numero se non intersecandola con alcuni concetti di geometria o spettanti alla geometria, che in questo caso pratica il giusto modo di operare sui numeri; modo che è assunto per molte argomentazioni e dimostrazioni che si fanno con le figure geometriche. Proprio in un altro libro che ho composto sulla pratica geometrica, spiegavo ciò che è pertinente alla geometria e a molte altre cose, descrivendolo con la singola figura, dimostrando ogni singola cosa con dimostrazioni geometriche poste sotto. Senz’altro questo libro spetta più alla teoria che alla pratica.Così chi volesse conoscere bene la pratica di questa scienza dovrà applicarsi con uso continuo ed esercizio giornaliero nella pratica di essa, perché se la conoscenza si muta in abitudine attraverso la pratica, la memoria e l’intelligenza concordano a tal punto con le mani e i segni che quasi in un unico impulso e anelito, in uno stesso istante, si accordano naturalmente su tutto; e allora quando il discepolo avrà conseguito un abito mentale, a poco a poco potrà pervenire facilmente alla perfezione di questa. E per rendere più facile la dottrina ho suddiviso questo libro in quindici capitoli, affinché il lettore possa più agevolmente rintracciare da essi qualsiasi cosa voglia. Inoltre se in questa opera si ravvisa qualche mancanza o difetto, li sottopongo alla vostra correzione. 		Importanza della geometria
(I.3 ; G: I.7) Quando mio padre fu nominato dalla patria pubblico scrivano nella dogana di Bugia per tutelare gli interessi dei mercanti pisani che vi affluivano, mi fece andare da lui, durante la mia fanciullezza, valutando l’utilità e il vantaggio futuro, e volle che mi fermassi lì per qualche tempo, per essere istruito nello studio dell’abbaco. Qui, introdotto nell’arte da uno straordinario insegnamento basato sulle nove figure degli Indiani mi piacque sopra ogni altra cosa, la conoscenza dell’arte e tanto compresi a suo riguardo che imparai con grande impegno e attraverso il contraddittorio delle dispute. qualunque cosa si studiasse di essa in Egitto, Siria, Grecia, Sicilia e Provenza con i loro diversi modi, luoghi di commercio in cui successivamente io mi recai spesso per affari. Ma io considerai addirittura tutto questo sapere e anche l’algoritmo e gli archi di Pitagora
(PdA)
Pictagore anziché Pythagor(a)e : la vocale y era stata tra le ultime lettere a entrare nell'alfabeto latino (sec.I a.C) [PdA,pag.1]
quasi un errore rispetto al metodo degli indiani. Quindi abbracciando in modo più stretto il metodo stesso degli Indiani e studiandolo più attentamente, aggiungendo in esso alcuni concetti in senso più specifico e inserendo anche alcune delle sottigliezze della geometria di Euclide, mi sono sforzato di comporre la totalità di questo libro, distinta in quindici capitoli, nel modo più comprensibile possibile dimostrando quasi tutto ciò che ho inserito con prove certe, affinché possano essere istruiti in questa scienza, con un metodo perfetto al di sopra di tutti gli altri, coloro che lo desiderano, e la gente latina d’altra parte, come accaduto finora, non vi si trovi del tutto esclusa. Se per caso ho inserito qualcosa meno o più del giusto o del necessario, vi prego di essere indulgenti con me, poiché non vi è alcuno che sia privo di difetti e che sia cauto in tutto sotto ogni aspetto. 		Note biografiche


Fine del prologo. Iniziano i capitoli
pg.2 (I.4 ; G: I.11)
  • Sulla conoscenza delle nove figure indiane, e come con esse si scriva ogni numero, e quali numeri, e come si debbano tenere sulle mani e introduzione dell’abaco
  • Sulla moltiplicazione dei numeri interi.
  • Sulla addizione dei numeri interi.
  • Sulla sottrazione di numeri minori da numeri maggiori.
  • Sulla divisione di numeri interi per numeri interi.
  • Sulla moltiplicazione di numeri interi per frazioni e di frazioni senza interi.
  • Sulla addizione, sottrazione e divisione di numeri interi con frazioni e riduzione delle parti dei numeri in singole parti.
  • Sull’acquisto e vendita di merci e simili.
  • Sui baratti delle merci, acquisto di bolzonaglie e alcune regole simili.
  • Sulle società fatte fra consoci.
  • Sulla fusione di monete e delle loro regole, pertinenti alla fusione.
  • Sulla soluzione di questioni di varia natura dette erratiche.
  • Sulla regola della doppia falsa posizione, come per essa si possano risolvere quasi tutte le varie questioni erratiche.
  • Sulla determinazione delle radici quadrate e cubiche e la moltiplicazione e divisione e somma e estrazione di queste radici tra di loro e dei recisi e delle loro radici.
  • Sulle regole e proporzioni pertinenti alla geometria: questioni di algebra e almuchabala.
 Indice del Liber abaci

Inizia il primo capitolo
(I.5 ; G: I.13) Le nove figure degli Indiani sono queste
987654321
I nove simboli indiani
per scrivere tutti i numeri
Pertanto con queste nove figure, e con questo segno 0, che gli Arabi chiamano zefiro, si scrive qualunque numero, come è mostrato più sotto. Infatti il numero è una raccolta fatta di unità o un insieme di unità, che per le sue posizioni sale all’infinito. La prima fra queste è formata dalle unità, che sono da uno fino a dieci. La seconda dalle decine che sono da dieci fino a cento. La terza si ha dalle centinaia che sono da cento fino a mille. La quarta dalle migliaia che sono da mille a diecimila, e così ognuna delle qualsiasi posizioni all’infinito consiste nel decuplo del suo antecedente. Nella scrittura dei numeri il primo posto comincia da destra. Il secondo invero, segue il primo verso sinistra. Il terzo segue il secondo. Il quarto il terzo, e il quinto il quarto, e sempre così verso sinistra un posto segue un posto. Pertanto la figura che si trova nel primo posto rappresenta se stessa, cioè se nel primo posto ci sarà la figura dell’uno esso rappresenta uno; se quello del due, due; se quello del tre, tre; e così nell’ordine che seguono fino a nove se c’è il nove: le nove figure poi che saranno nel secondo posto rappresentano tante decine quante nel primo le unità; cioè se la figura dell’unità occupa il secondo posto, indica dieci, se due, venti, se tre trenta, se nove, novanta. Scrittura posizionale
dei numeri interi
pg.3 (I.6 ; G: I.16) Infatti la figura che sarà nel terzo posto, indica tante centinaia, quante nel secondo le decine o nel primo e unità. E così la figura dell’unità [ indica ] cento; se due, duecento; se tre, trecento; e nove, novecento. Lo stesso dunque che si troverà nel quarto posto indica tante migliaia quante nel terzo le centinaia, o nel secondo le decine o nel primo le unità; e così sempre, mutando il posto, il numero sale moltiplicando per dieci.
(I.7 ; G: I.17) E affinché si mostri in modo più chiaro ciò che è stato detto, andiamo a illustrare il concetto stesso con le figure. Se la figura del sette sarà nel primo posto e del tre nel secondo, entrambi insieme rappresentano il 37; o al contrario: la figura del tre nel primo, e del sette nel secondo, ambedue insieme rappresentano il 73. Ancora se la figura del 4 sarà nella prima posizione e dell’unità in seconda così: 14, senza dubbio indicherà XIIII: oppure se la figura dell’uno sarà nella prima e del quattro nella seconda così: 41, indicherà XLI. Ancora, 7 al primo posto [NdT] La frase ci sembra mal trascritta
  e abbiamo tradotto secondo
  il senso che si impone. e 2 al secondo fanno 27; al contrario 2 nel primo e 7 nel secondo fa 72. Se figura del 7, così: 70; se ottanta, lo zefiro segua la figura dell’otto così 80: pertanto con questa dimostrazione puoi scrivere qualsivoglia numero da dieci fino a cento con due figure. Invece con tre si scrive da cento fino a mille; che se la figura dell’otto sarà nella prima posizione, e del cinque nella seconda, e dell’uno nella terza 158, sarà indicato il centocinquantotto; e al contrario: se la figura dell’uno sarà in prima posizione e del cinque in seconda e dell’otto in terza 851, indicheranno ottocentocinquantuno; o al contrario: se la figura dell’otto sarà nella prima posizione, e dell’uno in seconda e del cinque in terza, sarà denotato il 518. Ugualmente se cambiando, la figura del cinque sarà in prima posizione, dell’otto in seconda, e dell’uno in terza, sarà indicato il 185. Ugualmente se la figura dell’uno sarà nella prima, dell’otto nella seconda e del cinque in terza, certamente sarà indicato [ 581 ]; ma tre unità così 111, fanno centoundici. 		Esempi di
scrittura posizionale
(I.8 ; G: I.21) Ma se vorrai scrivere solo cinquecento, nella prima e seconda posizione poni gli zefiri, e nella terza la figura del cinque in questo modo: 500; e così con due zefiri potrai scrivere qualunque numero delle centinaia. E se vorrai scrivere le centinaia con le decine o le unità, poni in prima posizione lo zefiro, in seconda le decine e in terza le centinaia che vorrai. Per esempio: se in prima posizione ci fosse lo zefiro e nella seconda la figura del nove nella terza del due, indicheranno 290. Se invece vorrai scrivere senza decine le centinaia con le unità, porrai in seconda posizione, cioè al posto delle decine lo zefiro, e nella prima il numero delle unità che vorrai e nella terza delle centinaia: così nella prima posizione ci sarà la figura del nove e nella seconda lo zefiro e nel terzo quella del due 209; e così secondo la suddetta dimostrazione scriverai qualunque numero vorrai, da cento fino a mille con tre figure. E infatti con quattro da mille a diecimila, come si dimostra di seguito con le figure con i numeri soprascritti.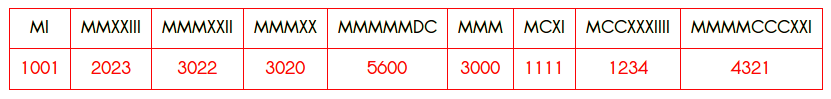


 Il ruolo dello zero
(I.9 ; G: I.23) E così si deve procedere nei restanti numeri. Infatti con cinque figure si scrivono tutti i numeri, cominciando da diecimila fino a centomila. Invece con sei, da centomila fino a mille migliaia, e così di seguito, aggiungendo una figura alle figure, il numero gradualmente sale di dieci. Per cui se capitasse che qualcuno non sia in grado di leggere o capire un qualche numero con molte figure per una gran quantità delle figure, procurerò di mostrare come si debba leggere e capire lo stesso.
pg.4 (I.10 ; G: I.24)
  • Pertanto, Della prima figura, cioè della figura in prima posizione, si dica uno
  • Della seconda, che è in seconda posizione, si dica dieci.
  • Della terza, che sarà al terzo posto, si dica cento, e la si accenti nella parte superiore
  • Della quarta figura poi dello stesso numero si dica mille, e la si accenti nella parte inferiore.
  • Della quinta si dica invece diecimila.
  • Della sesta pertanto centomila, e la si accenti nella parte superiore.
  • Della settima si dica mille migliaia, e lo si accenti di nuovo nella parte inferiore.
  • Dell’ottava si dica diecimila migliaia.
  • Della nona dica centomila migliaia, e lo si accenti nella parte superiore.
  • Della decima si dica mille migliaia di migliaia [ mille milioni ], e lo accenti nella parte inferiore.
E così sempre con questi tre numeri, cioè le migliaia, le decine di migliaia, e le centinaia di migliaia, accentando le migliaia nella parte inferiore, le centinaia di migliaia nella superiore, si abbia cura di accentare fino all’ultima posizione. E da qui si comincia a leggere il numero dall’ultima posizione dello stesso attraverso gli accenti menzionati, dicendo sempre dagli accenti inferiori tanti milioni quanti accenti siano davanti agli stessi nella parte inferiore verso la prima posizione, e leggendo dagli accenti superiori, tante centinaia di migliaia, quanti siano gli accenti davanti alla stessa nella parte inferiore verso la prima posizione; e di quelle figure che non sono state accentate dopo la quarta posizione del numero si leggano tante decine di migliaia, quante siano davanti a loro stesse nella parte inferiore; e così si potrà conoscere e leggere qualunque numero di molte figure. 		Come leggere numeri
comunque grandi
(I.11 ; G: I.28) E perché ciò si intenda meglio, proponiamo un numero di otto figure 87,´654,´321 [NdT] Abbiamo aggiunto gli accenti
  come indicato nel testo . . E così dell’uno che è in prima posizione si legga uno; del due 2 che è in seconda posizione si dica dieci, del tre 3 che è in terza si dica cento, e anche sono accentate nella parte superiore. Del quattro che è in quarta posizione si legga mille, che si accentano nella parte inferiore, come si mostra nel numero sopra scritto. Del cinque che è in quinta posizione si dica dieci migliaia; del sei che è in sesta posizione si dirà cento migliaia, che è accentata nella parte superiore; del sette che è in settima posizione si dirà in mille migliaia, ed è accentato nella parte inferiore; dell’otto che è in ultima posizione, si dirà dieci migliaia di migliaia. Dunque si ha nel numero sopra indicato ottantasette migliaia di migliaia per i due accenti inferiori, dei quali uno è sotto il sette e l’altro sotto il quattro, e inoltre seicentocinquantaquattromila, e poi CCCXXI. 		Come si legge
87,´654,´321

Matematica






pg.5 		(I.12 ; G: I.30) Ugualmente proponiamo un altro numero di nove figure 257,´604,´813, del quale, attraverso l’ordine degli accenti, si sa che in esso vi sono duecentocinquantasette migliaia di migliaia, e seicentoquattro migliaia, e ottocentotredici. Parimenti si proponga un altro numero di tredici figure 1,´007,´543,´289,´081, attraverso i cui accenti si riconosce che il numero stesso è mille, sette migliaia di migliaia di migliaia, e cinquecentoquarantatre migliaia di migliaia, e duecentoottantanovemila e ottantuno. Infatti possiamo riferire un’altra regola facile con cui potrai leggere un numero di più figure. Per esempio: proponiamo il numero di 15 figure : tralasciate le prime tre figure, cioè 296, sopra qualunque delle altre tre riporta una lineetta come un arco come nell’esempio prima esposto; e davanti a qualsiasi lineetta dirai [ migliaia ], e quelle tre figure che all’inizio hai tralasciato le leggerai come stanno; e così dirai seicentosettantotto migliaia di migliaia di migliaia di migliaia, poiché le lineette sono quattro e novecentotrentacinque migliaia di migliaia di migliaia, perché ci sono solo tre lineette e settecentottantaquattro migliaia di migliaia, essendoci due linee e 105 mila, perché c’è solo una lineetta, e 296 per quelle tre figure che all’inizio hai trascurato: e se dopo l’ultimo arco rimangono una o due figure, porrai le stesse sotto l’ultima lineetta, e leggerai tutte queste IIII o tutte e cinque insieme, e cosi potrai leggere un numero di tutte le figure che vorrai. Esempi di numeri
con più di 10 cifre

contare
con le mani 		(I.13 ; G: I.33) Ben apprese le figure suddette e le loro posizioni secondo la materia sopra descritta usandole frequentemente, è opportuno che quelli che vogliono usare l'arte dell’abaco, perché appaiano più abili e ingegnosi sappiano far di conto con i segni delle mani, escogitati in modo assai saggio nell’antichità secondo l’uso dei maestri d’abaco. Questi sono i segni. La curvatura del dito mignolo della mano sinistra sopra il centro del palmo della mano indica l’uno, a curvatura dello stesso con l’anulare similmente sopra il centro del palmo, indica due, quando con essi si curva il medio, indica tre. La curvatura poi dell’anulare e del medio similmente sopra il centro del palmo, indica quattro. Ma la curvatura soltanto del medio, cinque. Dell’anulare sei. E poi la posizione del mignolo verso l’alto sopra il palmo indica il sette, sopra questo posto quando si pone il mignolo e l’anulare si indica l’otto: la posizione dei medesimi con il medio sopra il medesimo posto, il 9. Quando dall’estremità dell’indice e dal pollice si fa un cerchio sul nodo del pollice, indica il dieci. Quando l’indice e il pollice sono dritti e si toccano, indicano 20. Quando dall’estremità degli stessi si fa un cerchio, il 30. Quando si pone il pollice sopra l’indice nella parte esterna dell’indice 40. La curvatura del pollice sopra l’inizio dell’indice 50. La curvatura dell’indice sopra il pollice curvato 60. La creatura dell’indice sopra l’estremità del pollice teso 70. E così la curvatura dell’indice sopra l’unghia del pollice teso, ottanta. Parimenti la curvatura di tutto l’indice su sé stesso 90. Anche le centinaia e le migliaia si formano sulla mano destra nel medesimo ordine, cioè il segno dell’uno sulla mano destra corrisponde a 100; del due allora 200; del dieci, invece, mille, e il segno del novanta, corrisponde a 9000, come si dimostra nella seguente pagina con i disegni delle mani. Dunque con le mani con questi segni si compongono tutti gli altri numeri che ci sono da dieci fino a diecimila in questo modo: dal segno del venti e dal segno del 3 si compone 23; e dal segno del tremila e dal segno del cinquecento si compongono sulla mano destra tremilacinquecento, e così capisci negli altri. Come rappresentare
i numeri con le mani

far di conto con le mani



pg.6

porte_del_piu.py

moltiplicazioni
cifra x cifra

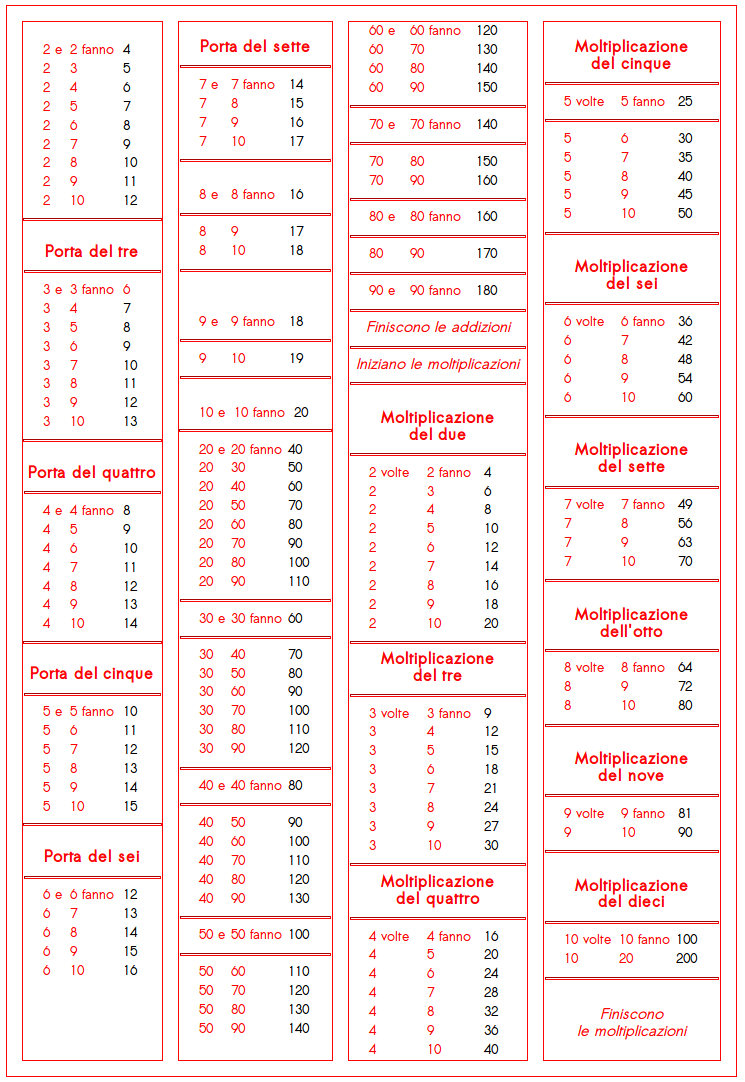
 		(T.1 ; G: I.37)
Introduzione nell’addizione e moltiplicazione dei numeri
pg.7 (I.14 ; G: I.44) E così imparando le somme e le moltiplicazioni scritte nelle tavole sempre facciano uso di raccogliere nelle mani, in modo che l’animo insieme alle mani divenga più veloce nelle addizioni e moltiplicazioni di qualsiasi numero.



Termina il primo capitolo.