|
|
|
|
|
|
La moltiplicazione tra numeri rotti.
Silvia Cerasaro
|
|
Dopo aver verificato le capacità di usare i numeri rotti, sino alla somma e alla differenza ed aver notato un impegno serio e spontaneo nello svolgere le operazioni date, siamo passati allo studio della moltiplicazione.
Dobbiamo calcolare il prodotto tra numeri rotti: visto che la moltiplicazione è un'addizione ripetuta, non dovrebbe essere difficile.
Le premesse sono sicuramente buone per affrontare l'operazione evitando di dare una regola mnemonica senza comprenderne il significato.
Ragazzi, conoscete già come fare delle semplici moltiplicazioni. Mi guardano attendendo di capire a cosa alludo.
Come costruite il numero rotto
3 5 con le aste?
Prendiamo 3 aste da
1 5,
quindi sappiamo già fare 3× 1 5, giusto?
Intendevo proprio questo, cioè definire nuovamente un multiplo
m di un rotto
1 n definendo
m n proprio come
m× 1 n,
facendo notare che allo stesso modo si può definire anche una frazione impropria.
|
|
Chiedo se conoscono un altro modo per definire
m n e mi fanno notare che è il modo che conoscono dalla scuola primaria per definire la frazione. L'alunna che mi ha dato questa risposta intendeva dire che si considera il numero m e lo dividiamo in n parti uguali otteniamo proprio
m n. Ad esempio,
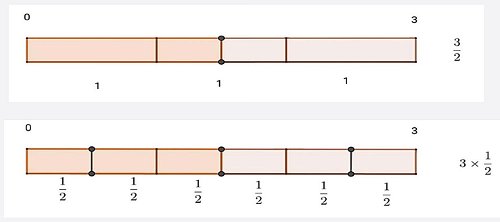
3 2 = 3 ×
1 2 ma
3 2 sulla retta dei numeri è 3:2.
|
|
|
Da questa puntualizzazione è emerso subito, anche alla luce di come abbiamo trattato la sottrazione, che la moltiplicazione e la divisione con i numeri rotti sono legate tra loro, non solo perché sono operazioni inverse. A rinforzo di questo, è stato proposto agli alunni di numerare per
1 n fino ad n, costruendo una sorta di tavola Pitagorica.
|
|
|
|
Inizialmente, gli alunni hanno numerato ottenendo anche numeri rotti riconducibili a rotti più piccoli, senza schisare perché concentrati a cercare numeri misti ed interi.
Da questa tavola, hanno notato la presenza di una diagonale con tutti 1,
quella nella quale si trova il risultato di n ×
1 n.
È stata poi data come consegna quella di riscriverla, con le opportune semplificazioni e scrivendo i numeri misti come frazioni improprie.
|
|
|
|
Così facendo, hanno notato delle caselle simmetriche rispetto la diagonale dei numeri 1 delle frazioni che scambiano il numeratore con il denominatore.
Abbiamo dato un nome a tali frazioni, le inverse o reciproche, ed hanno notato che il loro prodotto è 1.
Questo è un presupposto per svolgere la divisione in futuro perché se
a b ×
b a = 1, allora 1 :
b a =
a b.
|
|
A questo punto, tiro fuori dalla mia scatola l'asta unitaria, chiedendo agli alunni cosa rappresenta: tutti concordano, ovviamente, nel fatto che è l'intero da cui si ottengono i numeri rotti. Pongo, accanto all'asta unitaria, un quadrato di carta, avente proprio l'asta unitaria per lato.
Lo studio delle aree delle figure effettuato in geometria è sicuramente di grande aiuto per lo studio della moltiplicazione, poiché i ragazzi deducono abbastanza presto che il quadrato ha area 1 e che è un quadrato unitario da cui si potranno ottenere dei numeri rotti, dividendolo in parti uguali.
Qualcuno fa notare che queste parti sono differenti perchè una ha solo la lunghezza e l'altra ha pure la larghezza.
|
|
|
Allora, mostro loro questo strumento, chiedendomi di descriverlo. C'è un quadrato unitario ed i buchi per le aste unitarie, che vanno riempite.
|
In realtà, il fatto che "i buchi vanno riempiti dalle aste" non è stato compreso da tutti, in quanto chiedono come, così che mostro la seguente situazione.
|
|
Questo è uno strumento che ci aiuta a fare le moltiplicazioni con le frazioni, qui ad esempio, si vuole moltiplicare
1 2 ×
1 3.
Avete idee su come farlo?
La risposta non arriva subito, più che altro per paura di sbagliare perché, quando parlo di aree del quadrato o del rettangolo, mi dicono che l'area è il risultato di una moltiplicazione. Solo allora un alunno mi ha fa notare che 1 2 ×
1 3 è l'area di un rettangolo che ha i lati proprio di quelle misure. Dopo aver fatto notare la correttezza della sua risposta, chiedo loro di prendere delle squadrette per dividere il quadrato unitario in tante parti uguali, tante quante il prodotto dei denominatori.
Se svolgo
1 n ×
1 m, divido il quadrato in n righe e m colonne, ottenendo n × m rettangoli.
|
|
|
Nel nostro caso, si tracciano 2 righe e 3 colonne, ottenendo 6 rettangoli.
Il prodotto è il rettangolo che ha per lati le aste, in questo caso è 1 rettangolo su 6, quindi
1 6
|
|
Gli alunni comprendono molto presto il procedimento e svolgono molti esercizi con il materiale, eseguono moltiplicazioni tra rotti (frazioni proprie)
a n ×
b m.
Molto presto notano che il prodotto è
a × b n × m , cioè un numero rotto che ha al numeratore il prodotto dei numeratori e al denominatore il prodotto dei denominatori, eventualmente da schisare, cioè semplificare nel caso in cui il numeratore ed il denominatore abbiamo un divisore comune.
Solo dopo diverse lezioni qualche alunno più in gamba, usando la proprietà commutativa ( o sbirciando dal libro di testo) ha dedotto la semplificazione "a croce" che solitamente si insegna in maniera meccanica, sapendo spiegarmi, però, il motivo di questa scorciatoia.
|
|
In questo video, un alunno con qualche difficoltà in matematica ci spiega come fare la moltiplicazione, fiero di aver capito quanto trattato.
|
|
Gli alunni, oltre al materiale presentato per svolgere la moltiplicazione, hanno usato anche questo file GeoGebra  che funziona esattamente con lo stesso meccanismo, soprattutto per i compiti a casa, nei primi esercizi assegnati a rinforzo dell'apprendimento appena conseguito. che funziona esattamente con lo stesso meccanismo, soprattutto per i compiti a casa, nei primi esercizi assegnati a rinforzo dell'apprendimento appena conseguito.
|
|
|
|
Influenzati da quanto appreso sulla differenza tra rotti, affrontata come operazione inversa all'addizione, qualcuno ha esordito impostando una divisione come operazione inversa della moltiplicazione.
Se
3 4 ×
2 3 =
6 12 allora qual è quel numero che moltiplicato per
2 3 ci dà
6 12? Questo ci tornerà sicuramente utile per la divisione.
|
|
La moltiplicazione tra un numero rotto e un numero misto.
|
|
E se dovessimo calcolare il prodotto di un numero rotto per un misto?
Subito dopo, sarebbe ugualmente l'area di un rettangolo.
Si comincia con il piede giusto.
Calcoliamo
3 4 × ( 1 e
1 3).
Disegnamo un rettangolo di base 1 e
1 3e altezza
3 4, aiutiamoci con le aste. Potremmo anche scambiare la base con l'altezza, per la proprietà commutativa cambierà solo l'orientamento del rettangolo.
|
|
|
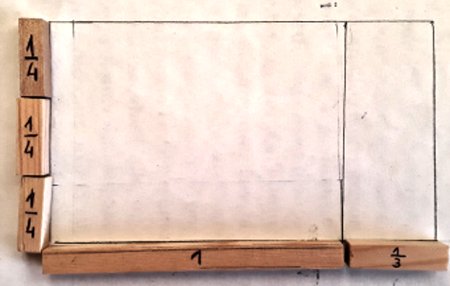
Il rettangolo è formato da 2 figure, la prima di dimensioni 1 e
3 4, la seconda di dimensioni
1 3 e
3 4.
Quindi,
3 4 × (1 e
1 3) =
3 4 × 1 + 3 4 × 1 3 =
3 4 +
3 12 =
3 4 +
1 4 =
4 4 = 1.
|
|
In questo video, un alunno esegue alla lavagna un prodotto tra un numero misto e un rotto.
|
|
La moltiplicazione tra misti.
|
|
Siamo passati, quindi, a studiare il prodotto tra numeri misti.
Alla luce della loro esperienza avuta finora sulla moltiplicazione, chiedo ai ragazzi come pensano di svolgere la moltiplicazione tra misti.
La loro risposta immediata è stata ridurre il numero misto in frazione impropria e moltiplicare tra loro i numeratori ed i denominatori. Metodologia sicuramente valida, ma speravo in una spiegazione "geometrica", che è arrivata in un secondo momento, solo dopo di aver chiesto di trovare una metodologia simile a quelle viste sia per il prodotto tra rotti che tra un rotto ed un misto.
Sarà sicuramente l'area di un rettangolo che ha per lati i numeri misti. Cominciamo così con degli esempi, per costruire il rettangolo cercato.
Calcoliamo 1 e
1 2 ×
2 e 2 3 con entrambe le metodologie: si ha
3 2 × 8 3 =
24 6 = 4.
Ora, con il metodo geometrico: si costruisce un rettangolo di dimensioni 1 e
1 2 e 2 e 2 3.
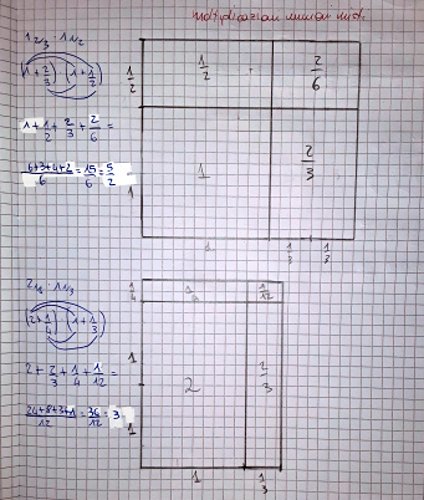
Cominciamo a provare a svolgere operazioni con questa metodologia, abbastanza veloce e pratica, e una delle alunne più volenterose verbalizza sul suo quaderno quanto segue.
|
|
Si mostra la costruzione del rettangolo descritta da questo file Geogebra  preparato precedentemente, dopo aver ricordato che la metodologia della costruzione è del tutto analoga a quella utilizzata nel prodotto tra un numero rotto e misto. preparato precedentemente, dopo aver ricordato che la metodologia della costruzione è del tutto analoga a quella utilizzata nel prodotto tra un numero rotto e misto.
|
|
|
|
Gli alunni inizialmente mostrano delle difficoltà nella suddivisione del rettangolo, così che si decide di fare tanti esercizi sul prodotto tra misti.
Resta presto immediato l'uso della proprietà distributiva, giustificato dalla presenza dei 4 rettangoli che suddividono quello iniziale.
|
|
Nelle lezioni seguenti, sono stati svolti molti esercizi, inizialmente con il metodo che ho definito geometrico, che va a rinforzare non solo le capacità spaziali nel vedere la suddivisione del rettangolo, ma va a favore anche del rinforzo dell'uso della proprietà distributiva, fondamentale per lo studio dell'algebra.
Quando sono stati svolti altri tipi di esercizi, gli alunni hanno utilizzato entrambi i metodi, prediligendo il primo metodo solo perché più veloce.
|
|
|
La divisione tra numeri rotti.
|
|
Il numero rotto è la divisione dell'intero in n parti uguali.
In questo modo abbiamo cominciato a trattare la divisione tra numeri rotti.
Abbiamo cominciato ad effettuare le divisioni "elementari " del tipo 1 : n =
1 n, che definiscono le frazioni unitarie.
Sono state poi svolte divisioni del tipo 1 : 1 n = n, usando le aste e costruendo nuovamente il muro dell'intero.
Cerco un numero che moltiplicato per
1 n mi dà 1, trovo n. E allora 1 diviso un numero rotto mi dà l'inverso.
Questa è una conclusione importante a cui i ragazzi sono arrivati dopo aver fatto diversi esempi grazie soprattutto al lavoro fatto precedentemente, basato sulla riflessione su quanto svolto e su esercizi che rendono il pensiero ed ogni forma di ragionamento reversibile.
Con questa nuova conoscenza, ho dato una divisione da svolgere, chiedendo come poter fare.
4 5 :
1 5. Semplice da fare perché noto i numeri di aste da
1 5 dentro
4 5, quindi fa 4.
Si continua. 4 5 :
8 15.
Non sanno come procedere perché il denominatore è diverso. Averlo notato così presto mi facilita il lavoro poiché suggerisco loro di fare in modo che il denominatore sia lo stesso.
Allora riduciamo in rotti più piccoli, come per l'addizione.
4 5 diventa
12 15, quindi
12 15 :
8 15. Ora hanno lo stesso denominatore ma come faccio 12 : 8?
L'alunna sembra avere difficoltà in quanto sembra non associare l'operazione della divisione alla frazione e sembra aver dimenticato quanto fatto per studiare i numeri misti. Con l'aiuto dei compagni, le torna in mente che 12 : 8 è 1
1 2, che in frazione impropria è
3 2.
Chiedo allora di formulare una regola e di appuntare quanto abbiamo detto dopo essersi consultati e dopo aver svolto altri esercizi.
|
|
Gli ultimi due esercizi di questa pagina riportano un metodo che gli alunni mi hanno descritto, dopo aver discusso a lungo tra loro per l'eventuale correttezza.
Mattia mi dice che trova più semplice questo metodo ed ha controllato l'esattezza del risultato procedendo come abbiamo fatto precedentemente.
Mi faccio spiegare.
Se devo svolgere 3 :
2 5 faccio prima 1 :
2 5 e poi moltiplico per 3.
So che 1 :
2 5 fa l'inverso di
2 5, cioè
5 2 o 2 e
1 2, e poi moltiplico per 3 ed ottengo
15 2, cioè 7 e
1 2.
In simboli, l'alunno dice che
n :
a b = n × (1 :
a b)= n ×
b a =
n b a.
Sono soddisfatta del ragionamento del mio alunno, che ho indotto a provare con un altro esempio.
3 4 ×(1 :
2 5) =
3 4 ×
5 2 =
15 8 = 1
7 8.
In simboli,
a b :
n m =
a b × (1 :
n m) =
a b ×
m n.
|

|
|
|
Le intuizioni dei ragazzi mi hanno indotto a far notare come passare dalla divisione alla moltiplicazione, quella che usualmente si trova sui libri di testo.
Ho lasciato i ragazzi liberi di usare uno dei metodi visti: alcuni preferiscono ridurre a numeri simiglianti, altri fare il procedimento per arrivare all'inverso.
Ho assegnato diversi esercizi per compito a casa, anche di tipo diverso.
Gli esercizi sono stati svolti senza nessuna difficoltà anche laddove erano presenti numeri misti, che i ragazzi hanno trasformato in frazioni improprie per fare gli opportuni conti.
|
|
Conclusioni
|
|
Trattare le frazioni come descrive i numeri rotti Fibonacci nel suo Liber abaci è sicuramente intuivo, perché avviene con la manipolazione di opportuno materiale, scrupolosamente costruito dagli alunni stessi.
Potrebbe sembrare lunga e meticolosa la trattazione della parte iniziale, relativa alla distinzione dei numeri rotti dai misti, come del resto anche quella dell’addizione, ma fondamentale per continuare lo studio delle altre operazioni.
Lo studio della moltiplicazione è la manifestazione della “geometrizzazione” dell’aritmetica mentre la divisione segue in maniera coerente la trattazione dei numeri rotti, avendo un procedimento in parte simile a quello dell’addizione, come definito dagli alunni, poiché si riduce in numeri simiglianti.
Gli esercizi svolti sono stati differenti dai consueti proposti per tale argomento: alle lunghe espressioni sono state presentate operazioni singole e sono state costruite tabelle da cui estrapolare fondamentali regole.
E’ stato compreso che un numero rotto, o razionale, è un numero presente sulla fitta retta dei numeri, differente da quello che era chiamato “operatore” nella scuola primaria e che stanno cominciando a trattare in maniera più approfondita in geometria con lo studio dei rapporti.
|
|