|
Didattica delle frazioni nelle classi 2B2 e 2C dell'IC AM Ricci Laura Tomassi |
||||||
|
Uno dei concetti matematici fondamentali, se non il più importante, che si forma nella mente dei ragazzi durante la scuola secondaria di primo grado è quello dei numeri razionali. Non possono essere però considerati solamente "un argomento", ma a ragione una struttura portante di tutto ciò che viene affrontato a partire dal secondo anno: i rapporti, le proporzioni, le percentuali, in geometria le similitudini, ma anche la formazione di prerequisiti dell'algebra, che caratterizzeranno tutto il percorso matematico dei ragazzi negli successivi.
In particolare in una delle due classi, la didattica è stata totalmente improntata al metodo di Fibonacci; nell'altra, all'inizio si è adottato un metodo più tradizionale: la scelta è dovuta a fattori strutturali della classe stessa. Infatti questo percorso è caratterizzato da tempi e criteri propri, dettati dai ritmi di apprendimento dei ragazzi non da programmi precostituiti. La scoperta richiede una disponibilità al ragionamento che a volte viene sopraffatta da un'abitudine consolidata alla regola semplice e già pronta; la grande attenzione al voto porta molti ad una smisurata ansia da prestazione e ad una impazienza, che mal si accorda con i tempi di questo percorso. In questa relazione verranno utilizzati immagini e video che sono sono stati realizzati in classe durante le quotidiane attività di laboratorio oppure spesso dai ragazzi a casa: la loro qualità può essere non molto alta, così come non vengono corretti su tutti gli errori e tutte le loro incertezze perché, anche se rifatti avrebbero certamente migliorato la loro qualità, sarebbero stati meno rappresentativi del percorso stesso , dei risultati e dei tempi a disposizione nella scuola pubblica per effettuare un lavoro di questo tipo. La maggior parte delle attività sono state realizzate facendo lavorare i ragazzi in gruppi di quattro, ciò ha reso l'ambiente della classe molto stimolante e vivace. |
||||||
|
|
||||||
|
I miei ragazzi conoscevano già il racconto di Fibonacci giovinetto che nel XIII secolo va ad imparare la matematica ed il commercio a Bugia…ma non sapevano il seguito di questa storia, cioè che per parlare di divisioni eque, Fibonacci capì che bisognava creare un nuovo strumento "a ciò che nisuno sia inganato": il calcolo frazionario. Il seguito della storia viene raccontato a partire dal V libro del Liber abaci, del quale alla Lim ho mostrato l'aspetto ed un frammento del testo. 

|
||||||
|
|
||||||
|
Le classi hanno cominciato lo studio delle frazioni già alla fine della classe prima riprendendo concetti appresi alla scuola primaria; sono stati utilizzati a tal fine dei materiali come i circoli montessoriani, che pur avendo il pregio di materializzare l'operazione di frazionamento, ponevano i loro limiti alla visualizzazione delle frazioni come numero, alla comprensione degli algoritmi di calcolo con le frazioni stesse e all'astrazione. A mio avviso, il limite percettivo più evidente di tale materiale è il fatto di visualizzare le frazioni come parti dell'angolo giro: per le frazioni improprie il materiale rischia di complicare le cose anziché semplificare la visualizzazione. Ad ogni modo, anche e soprattutto per questioni di tempo, nel primo anno si è solo introdotto il concetto di frazione, senza trattarne l'aritmetica, e per tale scopo il materiale è stato utilissimo. |
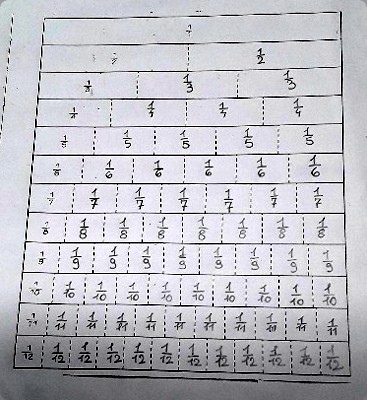
|
|||||

Fig.1 I primi materiali utilizzati: strisce di carta e asticelle gommate tagliate al laser.
|
Sono state realizzate dapprima delle strisce di carta ispirate alle aste montessoriane tagliate dai ragazzi come lavoro per casa; nel dare questo compito ho accennato all'idea che avrei realizzato del materiale con il legno. Una prima prova è stata fatta con carta gommata tagliata al laser (Fig.1). La prima reazione al materiale è stata di disappunto: la maggior parte pensava di non averne bisogno, soprattutto nel trattare un argomento che pensavano di "conoscere" già: "roba da piccoli". È bastato poco per dimostrare loro che in realtà la loro conoscenza era limitata e non ci si poteva fermare ad essa. |
|||||

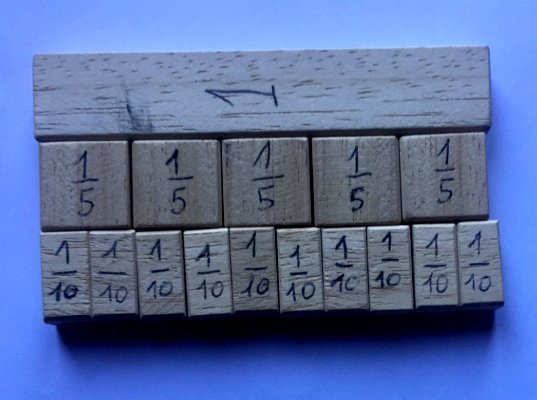
Fig.2 Le aste di Alessia
sul banco di lavoro del papà. |
Dopo un paio di settimane in cui utilizzavamo il materiale di carta, la sospresa più grande è stata che proprio nella classe in cui sembravano rifiutarlo di più, perché a loro dire troppo laborioso, un'alunna ha portato del materiale che ha fatto realizzare dal padre falegname e che viene utilizzata per gran parte delle attività (Fig.2). Si tratta di aste di legno di 10 cm frazionate dai decimi all'unità. La problematica associata a questo tipo di materiale, che ha per me comunque un significato speciale, perché ha testimoniato fiducia e stima nei confronti del nostro lavoro insieme, è di tipo fisico: la base delle asticelle non è quadrata ma rettangolare, come si noterà dalle immagini, questo particolare lo rende di difficile utilizzo con i rotti di piccola taglia, poiché ha presentato delle difficoltà nella manipolazione e nell'orientamento delle aste. Dopo un primo momento di disorientamento, i ragazzi hanno cominciato ad apprezzare lo stimolo visivo del materiale. |
|||||
|
|
||||||
|
Non è stato affatto scontato capire che : |
||||||
|
mn =
1n +
1n +
1n + .... = m ×
1n
|
||||||
|
Tradizionalmente sui libri di testo la frazione è rappresentata necessariamente come un "blocco unico", suddiviso in un certo numero di parti, del quale "se ne consideri una parte". Cosa diversa è stata considerarla un numero "rotto", fatto della somma di tante parti uguali, ciascuna con una sua individualità, dettata dal denominato la cui numerosità di volta in volta deve essere determinata dal denominante. La scoperta più interessante che i ragazzi hanno fatto è che nella nostra rappresentazione non è contenuto come in quella del libro "la cornice dell'unità che poi viene presa in un certo numero di parti": le nostre quantità sono rappresentate da mattoncini che possono cambiare le loro grandezza in base al "denominato" (Fig.3).
|

Fig.3 La rappresentazione di 1, 6/5, 1/4, 3/8
|
|||||
|
Chiamare i termini con la nomenclatura medioevale (denominato, denominante, rotto, sano) è stato sicuramente una riflessione linguistica efficace…un utile ritorno alle origini per capire la funzione numerica dei termini. Molto spesso ho scritto sulla lavagna indicazioni matematiche in italiano…senza numeri ,perché una delle caratteristiche più importanti del nostro percorso fibonacciano è stata la grande attenzione al lessico: stabilire un dizionario italiano matematica mi sembra uno dei mattoni più importanti nel passaggio dal percettivo al simbolico, che accompagni la loro crescita espressiva e di astrazione, nonché una delle problematiche di grande attualità, in un momento in cui la potenza espressiva delle parole è sostituita dall'immediatezza delle immagini.
|
||||||
|
|
||||||
|
Questo è stato il concetto ripetuto più volte con diverse attività, la più importante delle quali è sicuramente il fatto che i rotti sono numeri che possono essere scritti con una molteplicità di frazioni, tutte rappresentanti la stessa quantità.
|
||||||
|
|
||||||

|
|
|||||
|
Fig.4 Le frazioni equivalenti
|
||||||
|
Ci si è resi conto che si può rappresentare la stessa quantità utilizzando più frazioni che i ragazzi hanno definito "uguali"….ci siamo accordati sul fatto che non sono uguali ma equivalenti e che molto spesso nella pratica conviene utilizzare la frazione che "ha un minor numero di termini", perché in qualche modo è una rappresentazione più semplice di una data quantità: si è così dato un senso al termine "semplificare" che abbiamo anche chiamato "schisare".
Utilizzando la terminologia di Tartaglia…schisare è fare un segno sopra ai numeri per dire che "è equivalente ad un'altra più semplice". Ma si è anche posto l'accento sul fatto che è necessario di volta in volta stabilire quale frazione equivalente usare: "è come avere la stessa persona con vestiti diversi". È l'occasione particolare a decidere quale è meglio utilizzare. Questo dover scegliere è fondamentale per creare una forma di pensiero critica e non passiva. |
||||||
|
I ragazzi hanno cercato immediatamente la "regola aritmetica" (Fig.5) che permetta di ricavare frazioni equivalenti alle date. |

Fig.5 "Trova la regola aritmetica"
|
|||||
|
Vi sono stati diversi video, qui non riportati, che testimoniano grande difficoltà, in quanto, soprattutto studenti che hanno ha un voto di profitto alto, trasferiscono le loro nozioni nella manipolazione dei materiali e non il contrario e, a volte, si trovano in difficoltà nel trarre informazioni evidenti dagli stessi.
|
||||||
|
|
||||||
|
|
||||||
|
Inevitabilmente, se si è cercato di capire quando due rotti hanno lo stesso "valore", abbiamo cercato anche di confrontare il valore di due frazioni che non sono equivalenti. Gli esercizi, da realizzare con il materiale sono stati proposti in ordine di difficoltà crescente, ma da risolvere con manipolazione autonoma, evitando schemi ed imitazioni. Spesso è stato il loro comportamento a suggerirmi strategie, esempi e riflessioni. |
||||||
|
Come dice Chiara: "la frazione più grande è 3/5: la frazione con il denominatore più piccolo" (Fig.6)
|

Fig.6 Confronto tra 3/5, 3/6, 3/7
|
|||||
|
Come si vede dall'immagine (Fig.7), è stato spontaneo per i ragazzi andare a colmare ..le differenze!
|

Fig.7 Confronto fra 2/3 e 3/4
|
|||||
|
Nel video "Dal confronto alla differenza" si vede come Francesco spontaneamente passa dal concetto di confronto a quello di differenza: il bello di queste attività è che i concetti fondamentali del metodo di calcolo con le frazioni confluiscono l'uno nell'altro. Che questo sia successo per un'operazione inversa ( e di per sé complicata nella mente di un ragazzo) lo trovo di enorme importanza. Posso affermare che nel percorso fibonacciano "dall'operazione di confronto è emersa fluidamente quella di differenza e di somma".
È difficile in un percorso del genere che possa essere l'insegnante a decidere l'ordine in cui verrano affrontati gli argomenti: la sua funzione diventa molto importante però, perché la fluidità del percorso prevede grande forza guida nel pensare e capacità di riadattamento, ed è davvero stimolante per l'insegnante. |
||||||
|
|
||||||
|
|
||||||
|
…"quelle che non sono veramente una frazione" ( come dicono i ragazzi).
Li confonde il fatto di aver a che fare con una frazione ma con il gestire più di una unità o di un "sano", come hanno imparato a dire; inoltre nel leggere la frazione impropria non percepiscono l'ordine di grandezza del numero in termini di unità e quindi non si forma un'immagine immediata dell'effettiva grandezza della quantità rappresentata. L'ostacolo mentale è stato studiato e sorpassato con il numero misto: dà una idea molto più calzante di quanto una frazione impropria valga in realtà ( ad esempio "5/3 vale 1 ed un altro pezzetto è quindi un numero compreso tra 1 e 2"). In gruppi di quattro, ci siamo esercitati a trasformare il numero misto in frazione e la frazione in numero misto. Vero è che per alcuni il concetto di frazione impropria è rimasto, perché è cultura acquisita ormai dalla scuola primaria, però la manipolazione del materiale ha portato ad una visualizzazione più immediata e concreta dell'effettivo valore (come si vede e si sente dal video di alcuni studenti). |
||||||
|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
|
Si è cercato un algoritmo per fare sulla carta questo esercizio che noi abbiamo fatto con il materiale.
Lavorando con il materiale in gruppo hanno riportato quanto dedotto prima facendo i video, poi cercando di schematizzare e di verbalizzare sul quaderno. |
||||||
|
Le immagini che seguono sono gli elaborati di una esercitazione svolta in gruppo con il materiale: non sempre i ragazzi sono rigorosi, a volte tirano fuori delle regole non generalizzabili, però è significativo il fatto che procedano "visualizzando" le operazioni e non facendo solo calcoli. Dal numero misto alla frazione e da frazione a numero misto (Fig.8) : troviamo una regola. |
||||||
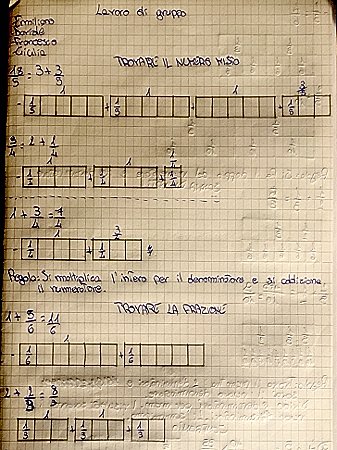 Fig.8 Frazione misto |
Dopo un po' il materiale diventa iconico: i ragazzi riproducono sul loro quaderno a casa le situazioni viste a scuola.
 Fig.9 |
|||||
|
|
||||||
|
Partendo da casi molto semplici, realizzabili con il materiale in dotazione, abbiamo realizzato diverse somme di rotti.
Ciò di cui ci si è convinti con grande facilità è che non è possibile, come verrebbe istintivo sommare numeratori e denominatori tra di loro. " I denominatori non si toccano: servono a dirci quanto sono grandi i pezzi" |
||||||
|
Dapprima abbiamo gestito somme con denominatori identici, poi siamo passati a quelle semplici come
12 +
14 o
13 +
16 ……
Abbiamo lavorato molto sul focalizzare e categorizzare ciò che la consegna ci sta richiedendo, perché l'operazione sia priva di automatismi: riconoscere i casi che si stanno studiando ed utilizzare la strategia più idonea. In seguito ci siamo spostati su problemi un pochino diversi come: calcolare la somma di
12 +
13 o di
12 +
25 o di
34 +
23.
|
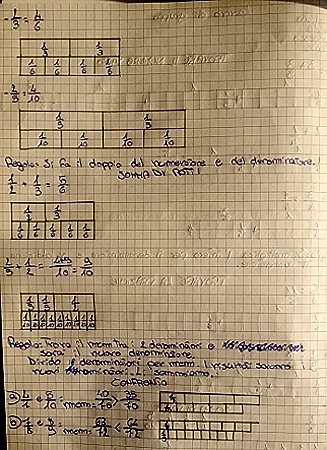 Fig.10 Esercitazione sulla somma |
|||||
|
Ci si è resi conto che che non è possibile esprimere la somma né utilizzando uno né tantomeno l'altro dei due denominatori: si devono "rispezzare" i rotti in maniera da averli tutti della stessa taglia … così bisogna andare a cercare dei rotti con stessa denominazione che siano correlati all'una e all'altra frazione da una relazione di equivalenza, ma che abbiano lo stesso denominato, due rotti simiglianti. Come abbiamo detto più volte"abbiamo vestito le frazioni" con il vestito "adatto all'occasione". Gli errori non sono stati corretti quando come denominatore hanno inserito un multiplo comune qualsiasi e non hanno cercato il minimo comune multiplo: viene introdotto in tempo successivo questo, come regola operativa utile e non come regola sostanziale. |
||||||
Le aste da 15 cm, con divisione dell'unità fino a 15, sono molto utili per farli ragionare sull'opportunità di cercare il minimo comune multiplo o "schisare", in seguito quando si eseguono somme come
56 +
12
Il problema però è che sui denominatori più grandi, come 12, 14, 15 si percepisce molto l'errore del taglio fatto a mano con sega e calibro, come si vede anche dalle immagini. La soluzione potrebbe essere quella di utilizzare aste con spessore inferiore e di tagliarle al laser. Sarebbero molto più precise.
|
||||||
Ad entrambe le classi è stato chiesto di realizzare un tabellone delle somme, analogo a quello realizzato da Fibonacci: a scuola in coppie e continuando il lavoro a casa. È stato singolare come abbiano preso questo lavoro a cuore i ragazzi …. Hanno fatto talmente tante somme che non è stato possibile metterle in cartellone. |
||||||
 Fig.11 Il Tabellone in costruzione |
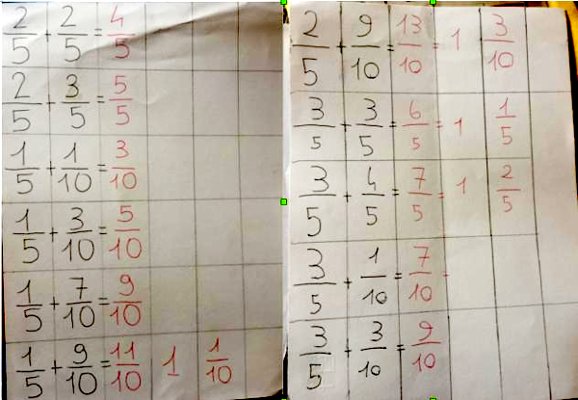 Fig.12 Somme realizzate dalla tabella di Fibonacci. |
|||||
Hanno realizzato dei piccoli fascicoli con carta da lucido bruciata sui bordi( che secondo loro richiamava la carta pergamena) rilegati con carta paglia, da appendere su un pannello in classe: LE TABULAE UTILISSIMAE SECONDACCII ( lo scherzo non manca mai nelle nostre giornate) (Fig.13). È piaciuta l'idea di un tabellone appeso in classe (Fig.14) che possa essere utilizzato come riferimento per eseguire i calcoli … anche se dopo qualche giorno il tabellone non veniva più neanche utilizzato perché molte somme le hanno mandate automaticamente in memoria. |
 Fig.13 Le TABULAE UTILISSIMAE SECONDACCII |
|||||
 Fig.14a Il Tabellone in classe |
 Fig.14b Le somme |
|||||
|
|
||||||
|
Abbiamo letto il seguente brano prima e dopo aver affrontato la moltiplicazione tra rotti: per loro è stato piuttosto misterioso all'inizio….
Maravigliati del atto di multiplicar di rotti,
(Tartaglia, General trattato (Parte Prima, Libro VII, c. 119)
perche in quello sempre si vede riuscire al contrario di quello che dinota tal vocabulo, qual non dinota altro che crescere, overo augumentare, & nel deto multplicare de rotti sempre seguita (come è detto) tutto al contrario, cioe che il produtto è sempre menore di qual si voglia di duoi precedenti..
Per questo argomento in un breve periodo di mia assenza le classi hanno conosciuto, ad opera di altri colleghi, nelle ore di supplenza, prima la regola operativa per la moltiplicazione. Le prime moltiplicazioni sono state introdotte attraverso semplici frasi in italiano, prive di simboli matematici, perché si riflettesse sul senso e sulla traduzione in linguaggio matematico di alcuni piccoli grandi problemi. Ho spiegato che fare un mezzo di una quantità è moltiplicare un mezzo per quella quantità ….. All'inizio non li ho convinti facilmente dell'equivalenza tra la preposizione "di" e l'operatore "×" . |
||||||
|
12 × 1 "significa prendere
12 una volta e viene un mezzo cioè la metà di 1"
Anche 12 × 3 posso trattare nella stessa maniera, come spiega Giulia nei video "Moltiplicare per 1/2" [ i filmati sono stati realizzati in autonomia con le sue compagne: lei dice di aver fatto delle autocorrezioni nel secondo video … Ritengo che anche questa idea dei ragazzi di autocorregersi sia fondamentale:anche se io non vedo differenze, inserisco entrambi i video per far capire come ci tengano anche a documentare quello che hanno fatto e comincino a cercare la maniera migliore "di dire le cose" ]. |
||||||
|
C'è da dire che questo percorso non è stato lineare: maturare consapevolezze matematiche di questo tipo ha richiesto la disponibilità mia e dei ragazzi a tornare sull'argomento diverse volte osservandolo da diversi aspetti e trovando l'attività appropriata a fornire "dimostrazioni" intuitive, poco formali ma generali e corrette. Per me è stato davvero affascinante, anche se non sempre semplice, fare questo tipo di ricerca.
|
||||||
|
n volte
12 cioè
n2, ma anche
12 di n.
Abbiamo fatto altri esempi:
12 di 5,
12 di
14.
15 per due significa
|
||||||
|
|
||||||
|
Un altro tipo di ragionamento fatto con i ragazzi è il seguente:
Quanto fa
12 ×
13 = ?
Per vedere il risultato devo prendere
12 e moltiplicarlo per 2 × 3, quindi sei volte
12 cioè 3; a questo punto il 3 è il numero di volte che prendo
13, cioè 1; quindi il numero a denominatore del prodotto è proprio il risultato di 2 × 3, cioè il prodotto dei denominatori.Mentre ad esempio 12 × 13 non fa 110 perché 10 × ( 12 × 13 ) = 102 × 13= 5 × 13 = 53 > 1 Siamo così arrivati a dire che 1n × 1m = 1n × m Il tipo di ragionamento fatto sopra però, sebbene li abbia portati a risolvere molte applicazioni ed esercizi, è stato quello su cui abbiamo riflettuto molto, ma ha suscitato molte perplessità nei miei studenti. |
||||||
 Fig.15 Il significato della moltiplicazione per un mezzo e per un terzo |
||||||

|

|

|
||||
| Fig.16 Esercizi per casa sulle moltiplicazioni: molto spesso gli esercizi per casa hanno previsto di verbalizzare ed ordinare quanto intuito con il materiale | ||||||
|
|
||||||
|
Una ulteriore interpretazione della moltiplicazione ha visto l'utilizzo di quadrati di legno 15 cm x 15 cm con aste da 15 cm suddivise in frazioni, dai mezzi fino ai quindicesimi.
I rotti fattori sono rappresentati sui lati di tali quadrati ed il prodotto è uguale all'area del rettangolo in essi contenuto, come frazione dell'area del quadrato (Fig. 17). |

|
|||||

|

|
|||||
|
Fig. 17 Alcuni momenti della risoluzione della moltiplicazione con l'utilizzo dei quadrati.
|
||||||
Nei video che seguono Silvia mostra il risultato di alcune moltiplicazioni.
|
||||||
|
Quando abbiamo trattato il prodotto tra frazioni come area del rettangolo, i ragazzini hanno manifestato la seguente perplessità quando li ho fatti riflettere sul fatto che il prodotto fosse minore delle frazioni di partenza: "non riusciamo a confrontare il rettangolo con i lati, sono cose diverse"; io facevo notare che sono gli interi ad essere diversi di natura…. Credo che questa loro perplessità abbia a che fare con il fatto che così facendo sto riportando la frazione al concetto di operatore: nell'affrontare i rotti, la parte più importante rimane sempre quella di far capire che sono "numeri", non parti di un intero .
L'osservazione delle proprietà della moltiplicazione diventa un esercizio di percezione e deduzione geometrica, di confronto tra aree ottenute in diverse situazioni. Molto questo esercizio ha aiutato anche nella comprensione delle aree, che è l'argomento di geometria centrale di questo anno.
Ad esempio i prodotti delle immagini diverse sono stati chiamati equivalenti in maniera spontanea dai ragazzi, facendo chiaramente riferimento all'area dei rettangoli risultato del prodotto di
14 × 1 e
12 ×
12.
|
||||||

|

|
|||||
|
Fig. 18 Prodotti equivalenti danno aree equivalenti
|
||||||
Il materiale è stato utilizzato anche per lo studio di semplici espressioni, con la guida di schede operative come questa riportata di seguito.
|
||||||
|
||||||
Quella che segue è invece l’elaborazione da parte dei ragazzi:
|
||||||
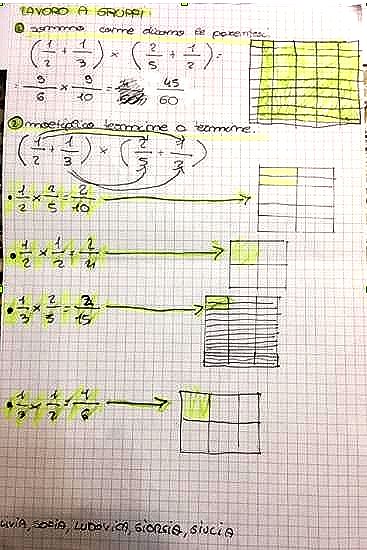 Fig. 20 aree equivalenti |
 Fig. 21 aree equivalenti (12+13)×(25+12) |
 Fig. 22 aree equivalenti 13×12 |
||||

|

|

|
||||
|
Fig. 23 aree equivalenti
12×12 |
Fig. 24 aree equivalenti
13×25 |
Fig. 25 aree equivalenti
[(13×12)+(13×25)] + [(12×12)+(12×25)] sovrapposto a area di Fig.21 |
||||
In questo lavoro le ragazze si sono convinte che i due procedimenti portano ad aree equivalenti ( l’ultima immagine rappresenta le aree singole ottenute da prodotto termine a termine, sovrapposta all’area iniziale totale contrassegnata nell apriam foto in azzurro)) e quindi hanno stabilito la validità della proprietà distributiva e gettato le basi per fare il prodotto tra numeri misti, nonché per affrontare in un secondo tempo l’argomento del prodotto tra binomi con scioltezza.
Raramente i nostri esercizi hanno riguardato lunghe espressioni: quasi sempre se vi sono state delle espressioni è per rifletterci su qualche proprietà come in questo caso.
|
||||||
|
|
||||||
L’operazione di sottrazione è stata già intuita quando si è fatto il confronto ed è stata subito individuata dai ragazzi come operazione inversa della somma; per questo, con grande perplessità da parte dei ragazzi che inizialmente pensavano di liquidare il tutto dicendo che la sottrazione si tratta come una somma, ho introdotto dei piccoli problemi riguardanti le sottrazioni come quello posto da Fibonacci : “da cosa fu sottratto un terzo che restò un quarto?”.
In questa maniera, che all’inizio li ha destabilizzati, in realtà si pone un problema fondamentale che è quello di individuare un’incognita che nei loro appunti compare sotto forma di punto interrogativo o di simbolo grafico. Si noti la diversa elaborazione grafica che le due studentesse hanno eseguito a casa per trovare il risultato: entrambe mostrano l’esigenza di trovare un’incognita. Questo è un notevole pregio del nostro percorso: introdurre delle esigenze logiche da risolvere con procedure che li portano a concetti che formalizzeranno meglio in seguito. Di fatto, la spontaneità con cui hanno in seguito risolto operazioni di differenza ha dimostrato che investire un consistente tempo nella manipolazione e nella sedimentazione di certezze visive dei concetti matematici porta a notevoli vantaggi, anche ma non solo temporali. |
||||||
 Fig. 26 I problemi con la sottrazione scritti a casa da Angela e Alessia. 
|
||||||
|
|
||||||
Nel trattare la moltiplicazione è stato evidenziato come questa per i rotti possa portare allo stesso risultato di una divisione per gli interi: ossia moltiplicare un numero per
12 è come dividerlo per 2, ossia per
21.
I ragazzi si sono accorti che le due operazioni hanno “una relazione particolare tra di loro”: dividere per un numero intero vuol dire moltiplicare per la frazione inversa.
Naturalmente per loro è stato un percorso abbastanza lento, graduale e fatto con i numeri, ma alla fine abbiamo generalizzato il concetto che in formule può essere espresso da:
ba = b ×
1a
"Dividere un numero b per a equivale a moltiplicare b con l’inverso di a". Siamo tornati sull’argomento diverse volte per poter “visualizzare” il processo logico che porta a questo. L’immagine sotto è uno dei tanti tentativi che abbiamo fatto.  Fig. 17 Dividere vuol dire moltiplicare per l’inverso; la “verbalizzazione” di Ludovica |
||||||
Il passaggio logico fondamentale che ci ha permesso di capire ha fatto riferimento al fatto che fare 2:3 significa dividere ogni unità per 3, cosa che loro hanno imparato a fare con le frazioni egizie e la disgregazione.
La divisione tra frazioni è stata affrontata in seguito nel seguente modo :
ab × b = a
a diviso b è quel numero che moltiplicato per b fa a
Come per la somma abbiamo imparato a dividere i due numeri in numeri con lo stesso denominatore e a quel punto è stato facile dedurre la divisione come divisione tra i numeratori.
|
||||||
Questo breve video illustra la divisione tra 4 e
23.
Si tenga presente che la realizzazione dei video, questo come il seguente, come anche altri, sono stati dati come compito per casa: sono imperfetti, ma testimoniano la necessità di razionalizzare e di spiegare, una cosa che molti compiti tradizionali non curano. |
||||||
In questo video Giorgia illustra il procedimento con il quale dividere
34 : 13 Per arrivare al risultato: 34 : 13 = 912 : 412 = = 9 : 4 = 94  |
||||||
|
|
||||||
Una cosa importante e significativa è che svolgere l’aritmetica delle frazioni ha portato le mie classi ad amare le nostre attività, la nostra vivacità e, se talvolta ci siamo sentiti indietro o diversi, perché i nostri quaderni non erano pieni di tante belle espressioni, quando ci siamo confrontati con le espressioni di prove di verifica tradizionali, non abbiamo sentito il disagio: è stato soltanto un ripetere in maniera ordinata ciò che sapevamo fare.
Un altra cosa importante è l’alta inclusività di un percorso di questo tipo che permette ai ragazzi con difficoltà di visualizzare ed imparare senza passare per il simbolismo, fermandosi fin dove serve per capire senza provare disagio.
Non so quanto un percorso come questo possa concludersi durante il secondo anno di una scuola media, se penso che io da insegnante ho imparato molto da tutto ciò e non parlo solo di metodo e didattica: andare all’origine delle cose mi ha portato a pensare anche molta matematica, molte cose fondamentali che a volte durante il mio percorso ho trascurato a favore di altre più complesse, ma meno importanti.
Sono sicura che i miei studenti non possano non beneficiare di questo. |
||||||
| | ||||||